天津市2020年空中课堂人教版八年级数学下册18.1.2 平行四边形的判定课件(共35张PPT)
文档属性
| 名称 | 天津市2020年空中课堂人教版八年级数学下册18.1.2 平行四边形的判定课件(共35张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-26 18:11:34 | ||
图片预览










文档简介
(共35张PPT)
18.1.2
平行四边形的判定
八年级
数学
学习目标
1.探索并证明平行四边形的判定定理:一组对边平行且相等的四边形是平行四边形;两组对边分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形;
2.探索并证明三角形的中位线定理.
一、复习回顾,引入新课
1.平行四边形的定义
两组对边分别平行的四边形叫做平行四边形.
(1)边:平行四边形的对边分别平行且相等;
(2)角:平行四边形的对角相等;
(3)对角线:平行四边形的对角线互相平分.
2.平行四边形的性质
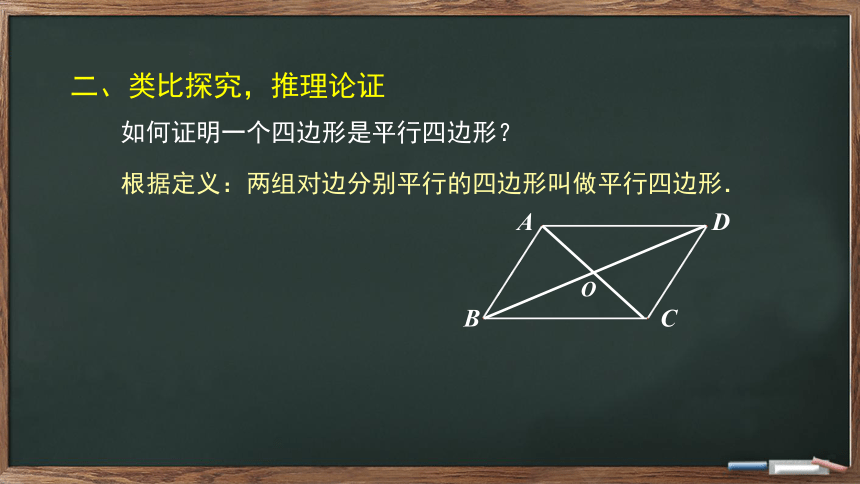
二、类比探究,推理论证
问题1
如何证明一个四边形是平行四边形呢?
根据定义“两组对边分别平行的四边形叫做平行四边形”可以判定一个四边形是平行四边形.
除了定义还有其他方法吗?
从性质定理的逆命题出发,研究平行四边形的判定方法.
二、类比探究,推理论证
平行四边形的性质
逆命题
平行四边形的两组对边分别相等
平行四边形的两组对角分别相等
平行四边形的对角线互相平分
两组对边分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形.
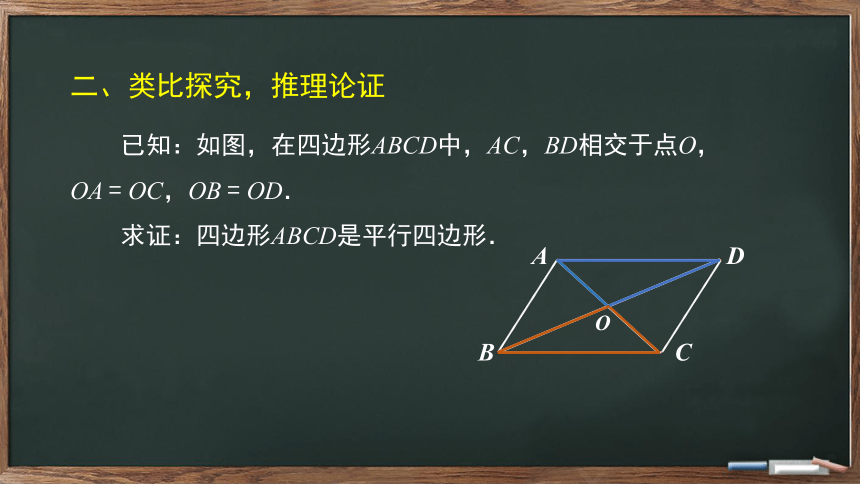
二、类比探究,推理论证
已知:如图,在四边形ABCD中,AC,BD相交于点O,OA
=
OC,OB
=
OD.
A
B
C
D
O
求证:四边形ABCD是平行四边形.
二、类比探究,推理论证
如何证明一个四边形是平行四边形?
根据定义:两组对边分别平行的四边形叫做平行四边形.
A
B
C
D
O
二、类比探究,推理论证
如何证明两条直线平行?
根据角的关系:
同位角相等,两直线平行;
内错角相等,两直线平行;
同旁内角互补,两直线平行.
A
B
C
D
O
已知:如图,在四边形ABCD中,AC,BD相交于点O,OA
=
OC,OB
=
OD.
求证:四边形ABCD是平行四边形.
A
B
C
D
O
二、类比探究,推理论证
A
B
C
D
O
二、类比探究,推理论证
证明:∵
OA
=
OC,OB
=
OD,
∠AOD
=∠COB,
∴
∠OAD
=∠OCB.
∴
△AOD
≌
△COB.
同理
AB∥DC.
∴
AD∥BC.
∴
四边形ABCD是平行四边形.
平行四边形的判定定理:
对角线互相平分的四边形是平行四边形.
二、类比探究,推理论证
平行四边形的性质
平行四边形的判定
平行四边形的两组对边分别相等
平行四边形的两组对角分别相等
平行四边形的对角线互相平分
两组对边分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
二、类比探究,推理论证
两组对边分别相等的四边形是平行四边形.
A
B
C
D
O
∵
AB
=
CD,BC
=
AD,
∴
四边形ABCD是平行四边形.
二、类比探究,推理论证
两组对角分别相等的四边形是平行四边形.
A
B
C
D
O
∵
∠ABC
=∠ADC,∠BAD
=∠BCD,
∴
四边形ABCD是平行四边形.
二、类比探究,推理论证
A
B
C
D
O
对角线互相平分的四边形是平行四边形.
∵
AO
=
CO,BO
=
DO,
∴
四边形ABCD是平行四边形.
O
F
E
D
B
A
C
例1
如图,□ABCD的对角线AC,BD相交于点O,E,F是AC上的两点,并且AE
=
CF.
求证:四边形BFDE是平行四边形.
二、类比探究,推理论证
O
F
E
D
B
A
C
证明:∵
四边形ABCD是平行四边形,
∵
AE
=
CF,
又
BO
=
DO
,
∴
四边形BFDE是平行四边形.
∴
AO
-
AE
=
CO
-
CF,即
EO
=
FO.
∴
AO
=
CO,BO
=
DO.
你还有其他证明方法吗?
二、类比探究,推理论证
O
F
E
D
B
A
C
例1
如图,□ABCD的对角线AC,BD相交于点O,E,F是AC上的两点,并且AE
=
CF
.
求证:四边形BFDE是平行四边形.
二、类比探究,推理论证
二、类比探究,推理论证
问题2
两组对边分别平行或相等的四边形是平行四边形.如果只考虑四边形的一组对边,它们满足什么条件时,这个四边形能成为平行四边形呢?
A
B
C
D
二、类比探究,推理论证
A
B
C
D
∵
四边形ABCD是平行四边形,∴
AB∥CD,AB
=
CD
.
反过来
∵
AB∥CD,AB
=
CD,
∴
四边形ABCD是平行四边形.
?
A
B
C
D
2
1
二、类比探究,推理论证
∴
∠1
=∠2.
∴△ABC
≌
△CDA.
∴
BC
=
DA.
∴
四边形ABCD是平行四边形.
又
AB
=
CD,AC
=
CA,
一组对边平行且相等的四边形是平行四边形
现在你有多少种判定一个四边形是平行四边形的方法?
∵
AB∥CD,
证明:连接AC.
二、类比探究,推理论证
归纳判定一个四边形是平行四边形的方法:
1.两组对边:两组对边分别平行的四边形叫做平行四边形;
2.两组对边:两组对边分别相等的四边形是平行四边形;
3.一组对边:一组对边平行且相等的四边形是平行四边形;
4.两组对角:两组对角分别相等的四边形是平行四边形;
5.对角线:对角线互相平分的四边形是平行四边形.
边
对角线
角
例2
如图,在□ABCD中,E,F分别是AB,CD的中点.求证:四边形EBFD是平行四边形.
证明:∵
四边形ABCD是平行四边形,
∴
四边形EBFD是平行四边形.
∴
EB
=
FD.
∴
AB
=
CD,EB∥FD
.
又
EB
=
AB,FD
=
CD,
A
F
E
D
C
B
二、类比探究,推理论证
三、换位探究,再获新知
如图,在△ABC中,D,E分别是AB,AC的中点,连接DE.像DE这样,连接三角形两边中点的线段叫做三角形的中位线.
D
E
C
B
A
A
B
C
F
F
D
E
三、换位探究,再获新知
问题3
观察下图,你能发现△ABC的中位线DE与边BC的位置关系吗?度量一下,DE与BC之间有什么数量关系?
D
E
C
B
A
猜想:DE∥BC,DE
=
BC.
E
D
C
B
A
三、换位探究,再获新知
如图,在△ABC中,D,E分别是AB,AC的中点.
求证:DE∥BC,且DE
=
BC.
D
E
C
B
A
F
E
D
C
B
A
∵
AE
=
EC,DE
=
EF,
又
DE
=
DF,
证明:延长DE到点F,使EF
=
DE,连接FC,DC,AF.
∴
四边形ADCF是平行四边形,
∴
DE∥BC,且DE
=
BC.
三、换位探究,再获新知
CF
DA.
∴
CF
BD.
∴
四边形DBCF是平行四边形,
DF
BC.
F
三、换位探究,再获新知
D
E
C
B
A
三角形的中位线定理:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
练习1
在△ABC中,D,E,F分别是AB,AC,BC的中点.以这些点为顶点,在图中,你能画出
个平行四边形.
四、运用新知,解决问题
D
E
C
B
A
F
3
四、运用新知,解决问题
练习2
如图,直线l1∥l2,在l1,l2上分别截取AD,BC,使AD
=
BC,连接AB,CD.
AB和CD有什么关系?为什么?
l2
l1
A
C
B
D
解:AB与CD平行且相等.
证明:∵
l1∥l2,
AD
=
BC,
∴
四边形ABCD是平行四边形,
∴
AB与CD平行且相等.
四、运用新知,解决问题
练习3
如图,□ABCD的对角线AC,BD相交于点O,E,F分别是OA,OC的中点.求证:BE
=
DF.
F
E
O
D
C
B
A
四、运用新知,解决问题
F
E
O
D
C
B
A
∴
AO
=
CO,BO
=
DO.
∴
四边形DEBF是平行四边形.
∵
E,F分别是OA,OC的中点,
证明:连接DE,BF.
∵
四边形ABCD是平行四边形,
∴
AO
=
2EO,CO
=
2FO.
∴
EO
=
FO.
∴
BE
=
DF.
五、课堂小结
判定一个四边形是平行四边形的方法
1.两组对边:两组对边分别平行的四边形叫做平行四边形;
两组对边分别相等的四边形是平行四边形;
2.一组对边:一组对边平行且相等的四边形是平行四边形;
3.两组对角:两组对角分别相等的四边形是平行四边形;
4.对角线:对角线互相平分的四边形是平行四边形.
三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
三角形的中位线定理
六、课后作业
教科书习题18.1,第4、5题.
六、课后作业
教科书习题18.1,第6、7题.
感谢收看,再见!
18.1.2
平行四边形的判定
八年级
数学
学习目标
1.探索并证明平行四边形的判定定理:一组对边平行且相等的四边形是平行四边形;两组对边分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形;
2.探索并证明三角形的中位线定理.
一、复习回顾,引入新课
1.平行四边形的定义
两组对边分别平行的四边形叫做平行四边形.
(1)边:平行四边形的对边分别平行且相等;
(2)角:平行四边形的对角相等;
(3)对角线:平行四边形的对角线互相平分.
2.平行四边形的性质
二、类比探究,推理论证
问题1
如何证明一个四边形是平行四边形呢?
根据定义“两组对边分别平行的四边形叫做平行四边形”可以判定一个四边形是平行四边形.
除了定义还有其他方法吗?
从性质定理的逆命题出发,研究平行四边形的判定方法.
二、类比探究,推理论证
平行四边形的性质
逆命题
平行四边形的两组对边分别相等
平行四边形的两组对角分别相等
平行四边形的对角线互相平分
两组对边分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形.
二、类比探究,推理论证
已知:如图,在四边形ABCD中,AC,BD相交于点O,OA
=
OC,OB
=
OD.
A
B
C
D
O
求证:四边形ABCD是平行四边形.
二、类比探究,推理论证
如何证明一个四边形是平行四边形?
根据定义:两组对边分别平行的四边形叫做平行四边形.
A
B
C
D
O
二、类比探究,推理论证
如何证明两条直线平行?
根据角的关系:
同位角相等,两直线平行;
内错角相等,两直线平行;
同旁内角互补,两直线平行.
A
B
C
D
O
已知:如图,在四边形ABCD中,AC,BD相交于点O,OA
=
OC,OB
=
OD.
求证:四边形ABCD是平行四边形.
A
B
C
D
O
二、类比探究,推理论证
A
B
C
D
O
二、类比探究,推理论证
证明:∵
OA
=
OC,OB
=
OD,
∠AOD
=∠COB,
∴
∠OAD
=∠OCB.
∴
△AOD
≌
△COB.
同理
AB∥DC.
∴
AD∥BC.
∴
四边形ABCD是平行四边形.
平行四边形的判定定理:
对角线互相平分的四边形是平行四边形.
二、类比探究,推理论证
平行四边形的性质
平行四边形的判定
平行四边形的两组对边分别相等
平行四边形的两组对角分别相等
平行四边形的对角线互相平分
两组对边分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
二、类比探究,推理论证
两组对边分别相等的四边形是平行四边形.
A
B
C
D
O
∵
AB
=
CD,BC
=
AD,
∴
四边形ABCD是平行四边形.
二、类比探究,推理论证
两组对角分别相等的四边形是平行四边形.
A
B
C
D
O
∵
∠ABC
=∠ADC,∠BAD
=∠BCD,
∴
四边形ABCD是平行四边形.
二、类比探究,推理论证
A
B
C
D
O
对角线互相平分的四边形是平行四边形.
∵
AO
=
CO,BO
=
DO,
∴
四边形ABCD是平行四边形.
O
F
E
D
B
A
C
例1
如图,□ABCD的对角线AC,BD相交于点O,E,F是AC上的两点,并且AE
=
CF.
求证:四边形BFDE是平行四边形.
二、类比探究,推理论证
O
F
E
D
B
A
C
证明:∵
四边形ABCD是平行四边形,
∵
AE
=
CF,
又
BO
=
DO
,
∴
四边形BFDE是平行四边形.
∴
AO
-
AE
=
CO
-
CF,即
EO
=
FO.
∴
AO
=
CO,BO
=
DO.
你还有其他证明方法吗?
二、类比探究,推理论证
O
F
E
D
B
A
C
例1
如图,□ABCD的对角线AC,BD相交于点O,E,F是AC上的两点,并且AE
=
CF
.
求证:四边形BFDE是平行四边形.
二、类比探究,推理论证
二、类比探究,推理论证
问题2
两组对边分别平行或相等的四边形是平行四边形.如果只考虑四边形的一组对边,它们满足什么条件时,这个四边形能成为平行四边形呢?
A
B
C
D
二、类比探究,推理论证
A
B
C
D
∵
四边形ABCD是平行四边形,∴
AB∥CD,AB
=
CD
.
反过来
∵
AB∥CD,AB
=
CD,
∴
四边形ABCD是平行四边形.
?
A
B
C
D
2
1
二、类比探究,推理论证
∴
∠1
=∠2.
∴△ABC
≌
△CDA.
∴
BC
=
DA.
∴
四边形ABCD是平行四边形.
又
AB
=
CD,AC
=
CA,
一组对边平行且相等的四边形是平行四边形
现在你有多少种判定一个四边形是平行四边形的方法?
∵
AB∥CD,
证明:连接AC.
二、类比探究,推理论证
归纳判定一个四边形是平行四边形的方法:
1.两组对边:两组对边分别平行的四边形叫做平行四边形;
2.两组对边:两组对边分别相等的四边形是平行四边形;
3.一组对边:一组对边平行且相等的四边形是平行四边形;
4.两组对角:两组对角分别相等的四边形是平行四边形;
5.对角线:对角线互相平分的四边形是平行四边形.
边
对角线
角
例2
如图,在□ABCD中,E,F分别是AB,CD的中点.求证:四边形EBFD是平行四边形.
证明:∵
四边形ABCD是平行四边形,
∴
四边形EBFD是平行四边形.
∴
EB
=
FD.
∴
AB
=
CD,EB∥FD
.
又
EB
=
AB,FD
=
CD,
A
F
E
D
C
B
二、类比探究,推理论证
三、换位探究,再获新知
如图,在△ABC中,D,E分别是AB,AC的中点,连接DE.像DE这样,连接三角形两边中点的线段叫做三角形的中位线.
D
E
C
B
A
A
B
C
F
F
D
E
三、换位探究,再获新知
问题3
观察下图,你能发现△ABC的中位线DE与边BC的位置关系吗?度量一下,DE与BC之间有什么数量关系?
D
E
C
B
A
猜想:DE∥BC,DE
=
BC.
E
D
C
B
A
三、换位探究,再获新知
如图,在△ABC中,D,E分别是AB,AC的中点.
求证:DE∥BC,且DE
=
BC.
D
E
C
B
A
F
E
D
C
B
A
∵
AE
=
EC,DE
=
EF,
又
DE
=
DF,
证明:延长DE到点F,使EF
=
DE,连接FC,DC,AF.
∴
四边形ADCF是平行四边形,
∴
DE∥BC,且DE
=
BC.
三、换位探究,再获新知
CF
DA.
∴
CF
BD.
∴
四边形DBCF是平行四边形,
DF
BC.
F
三、换位探究,再获新知
D
E
C
B
A
三角形的中位线定理:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
练习1
在△ABC中,D,E,F分别是AB,AC,BC的中点.以这些点为顶点,在图中,你能画出
个平行四边形.
四、运用新知,解决问题
D
E
C
B
A
F
3
四、运用新知,解决问题
练习2
如图,直线l1∥l2,在l1,l2上分别截取AD,BC,使AD
=
BC,连接AB,CD.
AB和CD有什么关系?为什么?
l2
l1
A
C
B
D
解:AB与CD平行且相等.
证明:∵
l1∥l2,
AD
=
BC,
∴
四边形ABCD是平行四边形,
∴
AB与CD平行且相等.
四、运用新知,解决问题
练习3
如图,□ABCD的对角线AC,BD相交于点O,E,F分别是OA,OC的中点.求证:BE
=
DF.
F
E
O
D
C
B
A
四、运用新知,解决问题
F
E
O
D
C
B
A
∴
AO
=
CO,BO
=
DO.
∴
四边形DEBF是平行四边形.
∵
E,F分别是OA,OC的中点,
证明:连接DE,BF.
∵
四边形ABCD是平行四边形,
∴
AO
=
2EO,CO
=
2FO.
∴
EO
=
FO.
∴
BE
=
DF.
五、课堂小结
判定一个四边形是平行四边形的方法
1.两组对边:两组对边分别平行的四边形叫做平行四边形;
两组对边分别相等的四边形是平行四边形;
2.一组对边:一组对边平行且相等的四边形是平行四边形;
3.两组对角:两组对角分别相等的四边形是平行四边形;
4.对角线:对角线互相平分的四边形是平行四边形.
三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
三角形的中位线定理
六、课后作业
教科书习题18.1,第4、5题.
六、课后作业
教科书习题18.1,第6、7题.
感谢收看,再见!
