天津市2020年空中课堂人教版八年级数学下册18.2.1 矩形课件(共30张PPT)
文档属性
| 名称 | 天津市2020年空中课堂人教版八年级数学下册18.2.1 矩形课件(共30张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-26 19:16:57 | ||
图片预览









文档简介
(共30张PPT)
18.2.1
矩形
八年级
数学
本课学习目标:
1.理解矩形的概念,明确矩形与平行四边形的区别和联系.
2.探索并证明矩形的性质,会用矩形性质解决相关问题.
3.探索并掌握“直角三角形斜边上的中线等于斜边的一半”这一重要结论.
4.探索并证明矩形的两个判定定理,能根据不同条件,运用定理.
5.经历矩形判定定理的猜想与证明过程,体会类比思想和图形判定探究的一般思路.
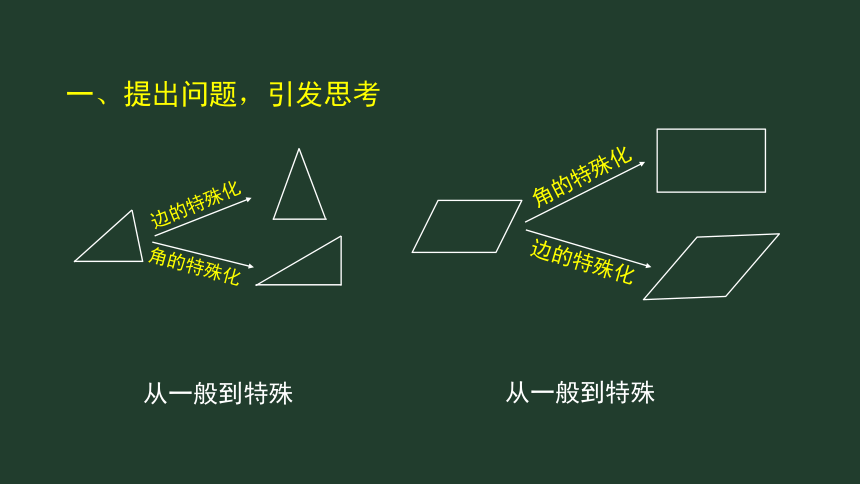
一、提出问题,引发思考
从一般到特殊
角的特殊化
边的特殊化
角的特殊化
边的特殊化
从一般到特殊
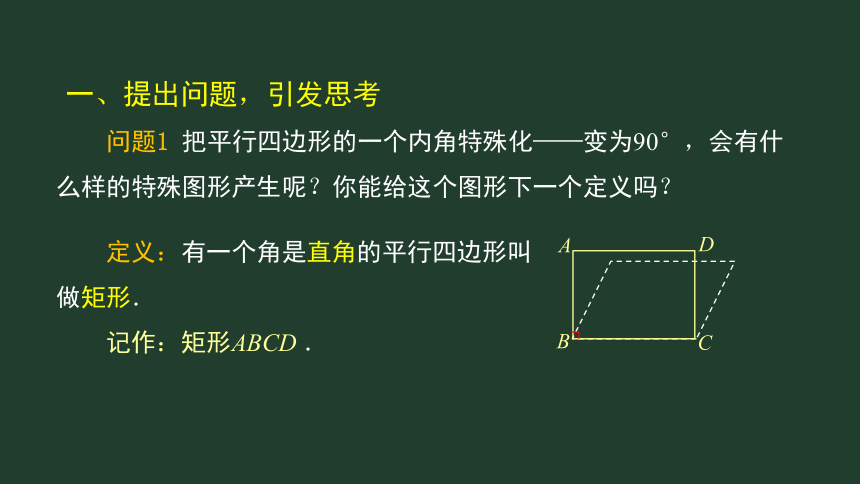
问题1
把平行四边形的一个内角特殊化——变为90°,会有什么样的特殊图形产生呢?你能给这个图形下一个定义吗?
定义:有一个角是直角的平行四边形叫做矩形.
记作:矩形ABCD
.
A
B
C
D
一、提出问题,引发思考
追问:你认为矩形有哪些性质?我们如何研究矩形的性质?
矩形是常见的图形.
一、提出问题,引发思考
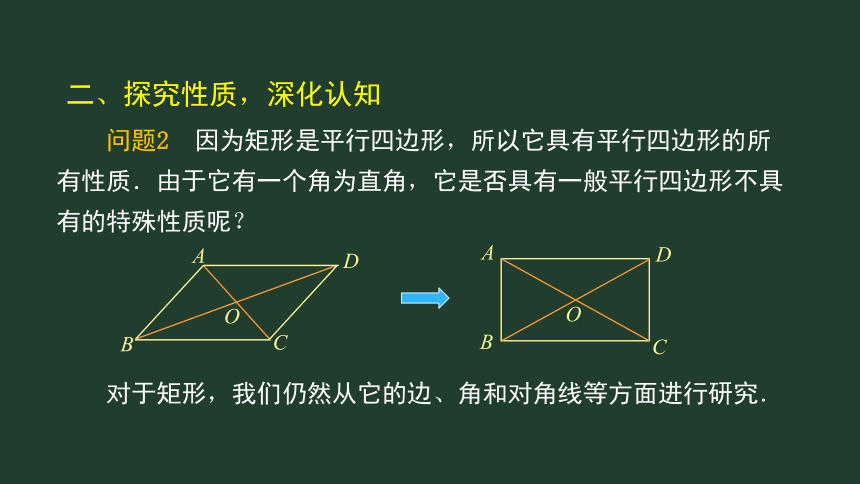
问题2
因为矩形是平行四边形,所以它具有平行四边形的所有性质.由于它有一个角为直角,它是否具有一般平行四边形不具有的特殊性质呢?
二、探究性质,深化认知
对于矩形,我们仍然从它的边、角和对角线等方面进行研究.
猜想1:矩形的四个角都是直角;
猜想2:矩形的对角线相等.
追问1:你能证明这些猜想吗?
二、探究性质,深化认知
猜想1:矩形的四个角都是直角.
已知:四边形ABCD是矩形.
求证:∠A=∠B=∠C=∠D=90?.
证明:∵
四边形ABCD是矩形,
∴
∠B=90?,AD∥BC,∠A=∠C,∠B=∠D.
∴
∠A=180?-∠B=90?.
∴
∠C=∠A=90?,∠D=∠B=90?.
∴
∠A=∠B=∠C=∠D=90?.
矩形的四个角都是直角.
二、探究性质,深化认知
猜想2:矩形的对角线相等.
已知:四边形ABCD是矩形.
求证:AC=BD.
证明:∵
四边形ABCD是矩形,
∴
∠ABC=∠DCB=90?,AB=DC.
又
BC是△ABC和△DCB的公共边,
∴
△ABC≌△DCB.
∴
AC=BD.
矩形的对角线相等.
二、探究性质,深化认知
矩形的性质小结:
边:矩形的对边平行且相等;
对角线:矩形的对角线相等且互相平分.
角:矩形的四个角都是直角;
二、探究性质,深化认知
A
B
C
D
矩形是轴对称图形.
它有两条对称轴,分别是对边中点连线所在的直线.
追问2:矩形是轴对称图形吗?
二、探究性质,深化认知
问题3
在前面的学习中,我们利用平行四边形的判定和性质研究了三角形的中位线,类似地,你能利用矩形的性质,探究直角三角形的一些特殊性质吗?
追问:如图,矩形ABCD的对角线AC,BD相交于点O,我们观察Rt△ABC,在Rt△ABC中,BO是斜边AC上的中线,BO与AC有什么关系?
二、探究性质,深化认知
直角三角形斜边上的中线等于斜边的一半.
二、探究性质,深化认知
三、运用性质,解决问题
例1
如图,矩形ABCD的对角线AC,BD相交于点O,∠AOB
=60°,AB=4,求矩形对角线的长.
解:∵
四边形ABCD是矩形,
∴
AC与BD相等且互相平分.
∴
OA=OB.
又
∠AOB=60?,
∴
△OAB是等边三角形.
∴
OA=AB=4.
∴
AC=BD=2OA=8.
例2
如图,四边形ABCD是矩形,AE∥BD
,且交CB的延长线于点E.求证:∠EAB=∠CAB
.
证明:∵
四边形ABCD是矩形,
∴
AC与BD相等且互相平分.
∴
OA=OB.
∴
∠OAB=∠OBA.
∵
AE∥BD,
∴
∠EAB=∠OBA
.
∴
∠EAB=∠CAB
.
你还有其它证明方法吗?
三、运用性质,解决问题
证明:∵
四边形ABCD是矩形,
∴
AC=BD,AD∥BC,∠ABC=90?.
∵
AE∥BD,且交CB的延长线于点E,
∴
四边形AEBD是平行四边形.
∴
AE=BD
.
∴
AC=AE.
∴
∠EAB=∠CAB
.
例2
如图,四边形ABCD是矩形,AE∥BD
,且交CB的延长线于点E.求证:∠EAB=∠CAB
.
三、运用性质,解决问题
问题4
由矩形的定义可知,有一个角是直角的平行四边形是矩形.除此之外,还有没有其他判定方法呢?
四、类比学习,得到判定
与研究平行四边形的判定方法类似,我们研究矩形性质定理的逆命题,看看它们是否成立.
追问1:我们知道,矩形的对角线相等.反过来,对角线相等的平行四边形是矩形吗?
已知:在□ABCD中,AC=BD.
求证:□ABCD是矩形.
四、类比学习,得到判定
已知:在□ABCD中,AC=BD.
求证:□ABCD是矩形.
证明:∵
四边形ABCD是平行四边形,
∴
AB=DC,AB∥DC.
∴
∠ABC+∠DCB=180?.
∵
AC=DB,
BC是△ABC和△DCB的公共边,
∴
△ABC≌△DCB.
∴
∠ABC=∠DCB.
∴
∠ABC=90?.
∴
□ABCD是矩形.
对角线相等的平行四边形是矩形.
四、类比学习,得到判定
追问2:前面我们研究了矩形的四个角,知道它们都是直角,它的逆命题成立吗?即四个角都是直角的四边形是矩形吗?进一步,至少有几个角是直角的四边形是矩形?
四、类比学习,得到判定
已知:在四边形ABCD中,∠A=∠B=∠C=90?.
求证:四边形ABCD是矩形.
证明:∵
∠A=∠B=∠C=90?,
∴
∠A+∠B=180?,∠B+∠C=180?.
∴
AD∥BC,AB∥CD.
∴
四边形ABCD是平行四边形.
又
∠A=90?,
∴
四边形ABCD是矩形.
有三个角是直角的四边形是矩形.
四、类比学习,得到判定
有三个角是直角
矩形的判定方法小结:
有一个角是直角
对角线相等
矩形
平行四边形
四边形
四、类比学习,得到判定
五、运用新知,解决问题
问题5
工人师傅制作了一个窗户的框架,你能利用直尺和三角板帮他检验一下所做的框架为矩形吗?
在判断框架是否为矩形的过程中,能否用下列方法完成?为什么?
(1)有一个角是直角的四边形是矩形;
不能证明是矩形.
(2)四个角都相等的四边形是矩形;
(3)对角线相等的四边形是矩形;
(4)两组对边分别相等,且对角线相等的四边形是矩形.
能证明是矩形.因为四边形的内角和是360?,四个角都相等,所以每个角都是直角.符合有三个角是直角的四边形是矩形.
不能证明是矩形.
能证明是矩形.因为两组对边分别相等的四边形是平行四边形,所以符合对角线相等的平行四边形是矩形.
四、类比学习,得到判定
五、运用新知,解决问题
例3
如图,在□ABCD中,对角线AC,BD相交于点O,且OA=OD,∠OAD=50°.求∠OAB的度数.
∴
∠DAB=90?.
又
∠OAD=50?,
∴
∠OAB=40?.
六、归纳整理,形成体系
1.矩形有哪些性质?它是轴对称图形吗?能否从轴对称角度说说矩形区别于一般平行四边形的特殊性质?
矩形的对边平行且相等;
矩形的对角线相等且互相平分.
矩形的四个角都是直角;
矩形是轴对称图形.
矩形的对角线相等且互相平分
矩形的四个角都是直角;
2.用矩形性质可以得到直角三角形的什么性质?
直角三角形斜边上的中线等于斜边的一半.
六、归纳整理,形成体系
3.矩形的判定有几种方法?在具体问题中,如何选择这些方法?
方法一:有一个角是直角的平行四边形是矩形.
方法二:对角线相等的平行四边形是矩形.
方法三:有三个角是直角的四边形是矩形.
有一个角是直角
对角线相等
矩形
平行四边形
矩形
有三个角是直角
四边形
有一个角是直角的平行四边形
对角线相等的平行四边形
有三个角是直角的四边形
六、归纳整理,形成体系
七、布置作业
教材60页,第1、2、3、4题.
同学们再见!
18.2.1
矩形
八年级
数学
本课学习目标:
1.理解矩形的概念,明确矩形与平行四边形的区别和联系.
2.探索并证明矩形的性质,会用矩形性质解决相关问题.
3.探索并掌握“直角三角形斜边上的中线等于斜边的一半”这一重要结论.
4.探索并证明矩形的两个判定定理,能根据不同条件,运用定理.
5.经历矩形判定定理的猜想与证明过程,体会类比思想和图形判定探究的一般思路.
一、提出问题,引发思考
从一般到特殊
角的特殊化
边的特殊化
角的特殊化
边的特殊化
从一般到特殊
问题1
把平行四边形的一个内角特殊化——变为90°,会有什么样的特殊图形产生呢?你能给这个图形下一个定义吗?
定义:有一个角是直角的平行四边形叫做矩形.
记作:矩形ABCD
.
A
B
C
D
一、提出问题,引发思考
追问:你认为矩形有哪些性质?我们如何研究矩形的性质?
矩形是常见的图形.
一、提出问题,引发思考
问题2
因为矩形是平行四边形,所以它具有平行四边形的所有性质.由于它有一个角为直角,它是否具有一般平行四边形不具有的特殊性质呢?
二、探究性质,深化认知
对于矩形,我们仍然从它的边、角和对角线等方面进行研究.
猜想1:矩形的四个角都是直角;
猜想2:矩形的对角线相等.
追问1:你能证明这些猜想吗?
二、探究性质,深化认知
猜想1:矩形的四个角都是直角.
已知:四边形ABCD是矩形.
求证:∠A=∠B=∠C=∠D=90?.
证明:∵
四边形ABCD是矩形,
∴
∠B=90?,AD∥BC,∠A=∠C,∠B=∠D.
∴
∠A=180?-∠B=90?.
∴
∠C=∠A=90?,∠D=∠B=90?.
∴
∠A=∠B=∠C=∠D=90?.
矩形的四个角都是直角.
二、探究性质,深化认知
猜想2:矩形的对角线相等.
已知:四边形ABCD是矩形.
求证:AC=BD.
证明:∵
四边形ABCD是矩形,
∴
∠ABC=∠DCB=90?,AB=DC.
又
BC是△ABC和△DCB的公共边,
∴
△ABC≌△DCB.
∴
AC=BD.
矩形的对角线相等.
二、探究性质,深化认知
矩形的性质小结:
边:矩形的对边平行且相等;
对角线:矩形的对角线相等且互相平分.
角:矩形的四个角都是直角;
二、探究性质,深化认知
A
B
C
D
矩形是轴对称图形.
它有两条对称轴,分别是对边中点连线所在的直线.
追问2:矩形是轴对称图形吗?
二、探究性质,深化认知
问题3
在前面的学习中,我们利用平行四边形的判定和性质研究了三角形的中位线,类似地,你能利用矩形的性质,探究直角三角形的一些特殊性质吗?
追问:如图,矩形ABCD的对角线AC,BD相交于点O,我们观察Rt△ABC,在Rt△ABC中,BO是斜边AC上的中线,BO与AC有什么关系?
二、探究性质,深化认知
直角三角形斜边上的中线等于斜边的一半.
二、探究性质,深化认知
三、运用性质,解决问题
例1
如图,矩形ABCD的对角线AC,BD相交于点O,∠AOB
=60°,AB=4,求矩形对角线的长.
解:∵
四边形ABCD是矩形,
∴
AC与BD相等且互相平分.
∴
OA=OB.
又
∠AOB=60?,
∴
△OAB是等边三角形.
∴
OA=AB=4.
∴
AC=BD=2OA=8.
例2
如图,四边形ABCD是矩形,AE∥BD
,且交CB的延长线于点E.求证:∠EAB=∠CAB
.
证明:∵
四边形ABCD是矩形,
∴
AC与BD相等且互相平分.
∴
OA=OB.
∴
∠OAB=∠OBA.
∵
AE∥BD,
∴
∠EAB=∠OBA
.
∴
∠EAB=∠CAB
.
你还有其它证明方法吗?
三、运用性质,解决问题
证明:∵
四边形ABCD是矩形,
∴
AC=BD,AD∥BC,∠ABC=90?.
∵
AE∥BD,且交CB的延长线于点E,
∴
四边形AEBD是平行四边形.
∴
AE=BD
.
∴
AC=AE.
∴
∠EAB=∠CAB
.
例2
如图,四边形ABCD是矩形,AE∥BD
,且交CB的延长线于点E.求证:∠EAB=∠CAB
.
三、运用性质,解决问题
问题4
由矩形的定义可知,有一个角是直角的平行四边形是矩形.除此之外,还有没有其他判定方法呢?
四、类比学习,得到判定
与研究平行四边形的判定方法类似,我们研究矩形性质定理的逆命题,看看它们是否成立.
追问1:我们知道,矩形的对角线相等.反过来,对角线相等的平行四边形是矩形吗?
已知:在□ABCD中,AC=BD.
求证:□ABCD是矩形.
四、类比学习,得到判定
已知:在□ABCD中,AC=BD.
求证:□ABCD是矩形.
证明:∵
四边形ABCD是平行四边形,
∴
AB=DC,AB∥DC.
∴
∠ABC+∠DCB=180?.
∵
AC=DB,
BC是△ABC和△DCB的公共边,
∴
△ABC≌△DCB.
∴
∠ABC=∠DCB.
∴
∠ABC=90?.
∴
□ABCD是矩形.
对角线相等的平行四边形是矩形.
四、类比学习,得到判定
追问2:前面我们研究了矩形的四个角,知道它们都是直角,它的逆命题成立吗?即四个角都是直角的四边形是矩形吗?进一步,至少有几个角是直角的四边形是矩形?
四、类比学习,得到判定
已知:在四边形ABCD中,∠A=∠B=∠C=90?.
求证:四边形ABCD是矩形.
证明:∵
∠A=∠B=∠C=90?,
∴
∠A+∠B=180?,∠B+∠C=180?.
∴
AD∥BC,AB∥CD.
∴
四边形ABCD是平行四边形.
又
∠A=90?,
∴
四边形ABCD是矩形.
有三个角是直角的四边形是矩形.
四、类比学习,得到判定
有三个角是直角
矩形的判定方法小结:
有一个角是直角
对角线相等
矩形
平行四边形
四边形
四、类比学习,得到判定
五、运用新知,解决问题
问题5
工人师傅制作了一个窗户的框架,你能利用直尺和三角板帮他检验一下所做的框架为矩形吗?
在判断框架是否为矩形的过程中,能否用下列方法完成?为什么?
(1)有一个角是直角的四边形是矩形;
不能证明是矩形.
(2)四个角都相等的四边形是矩形;
(3)对角线相等的四边形是矩形;
(4)两组对边分别相等,且对角线相等的四边形是矩形.
能证明是矩形.因为四边形的内角和是360?,四个角都相等,所以每个角都是直角.符合有三个角是直角的四边形是矩形.
不能证明是矩形.
能证明是矩形.因为两组对边分别相等的四边形是平行四边形,所以符合对角线相等的平行四边形是矩形.
四、类比学习,得到判定
五、运用新知,解决问题
例3
如图,在□ABCD中,对角线AC,BD相交于点O,且OA=OD,∠OAD=50°.求∠OAB的度数.
∴
∠DAB=90?.
又
∠OAD=50?,
∴
∠OAB=40?.
六、归纳整理,形成体系
1.矩形有哪些性质?它是轴对称图形吗?能否从轴对称角度说说矩形区别于一般平行四边形的特殊性质?
矩形的对边平行且相等;
矩形的对角线相等且互相平分.
矩形的四个角都是直角;
矩形是轴对称图形.
矩形的对角线相等且互相平分
矩形的四个角都是直角;
2.用矩形性质可以得到直角三角形的什么性质?
直角三角形斜边上的中线等于斜边的一半.
六、归纳整理,形成体系
3.矩形的判定有几种方法?在具体问题中,如何选择这些方法?
方法一:有一个角是直角的平行四边形是矩形.
方法二:对角线相等的平行四边形是矩形.
方法三:有三个角是直角的四边形是矩形.
有一个角是直角
对角线相等
矩形
平行四边形
矩形
有三个角是直角
四边形
有一个角是直角的平行四边形
对角线相等的平行四边形
有三个角是直角的四边形
六、归纳整理,形成体系
七、布置作业
教材60页,第1、2、3、4题.
同学们再见!
