天津市2020年空中课堂人教版八年级数学下册18.2.3 正方形课件(共28张PPT)
文档属性
| 名称 | 天津市2020年空中课堂人教版八年级数学下册18.2.3 正方形课件(共28张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 909.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-26 19:20:18 | ||
图片预览





文档简介
(共28张PPT)
18.2.3
正方形
八年级
数学
学习目标:
1.理解正方形的概念,以及与平行四边形、矩形、菱形之间的关系.
2.探索正方形的性质定理和判定定理,并能运用它们进行证明和计算.
一组邻
边相等
平行
四边形
矩形
菱形
一个角
是直角
一、复习引入
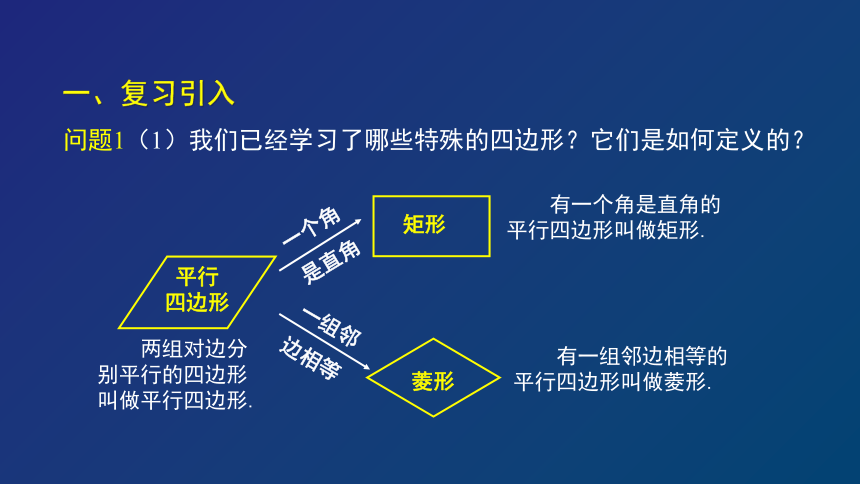
两组对边分别平行的四边形叫做平行四边形.
问题1(1)我们已经学习了哪些特殊的四边形?它们是如何定义的?
有一个角是直角的平行四边形叫做矩形.
有一组邻边相等的平行四边形叫做菱形.
问题1(2)我们是如何研究这些图形的?
定义
性质
边
角
对角线
判定
一、复习引入
问题2
在小学,我们还学习过什么特殊的平行四边形?
正方形
正方形的四条边都相等,四个角都是直角.
一、复习引入
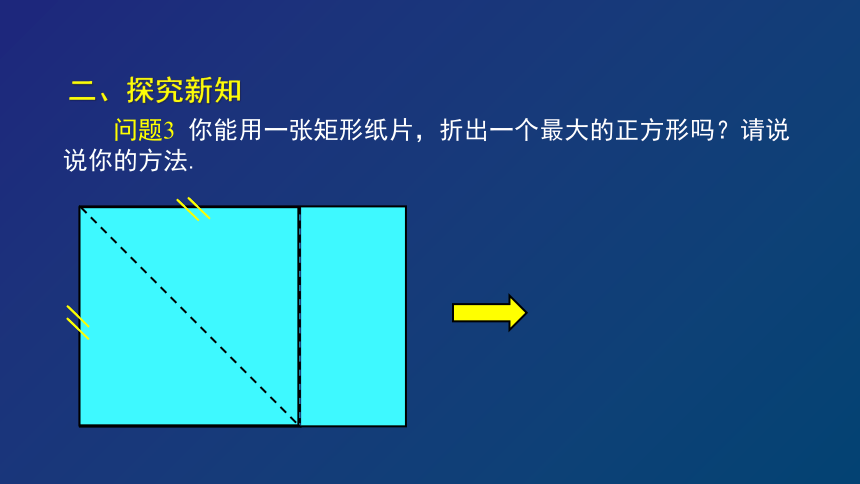
问题3
你能用一张矩形纸片,折出一个最大的正方形吗?请说说你的方法.
二、探究新知
问题4
菱形具有怎样的条件才能是正方形呢?
正方形
二、探究新知
邻边相等
〃
〃
〃
正方形
〃
菱形
一个角
是直角
正方形
∟
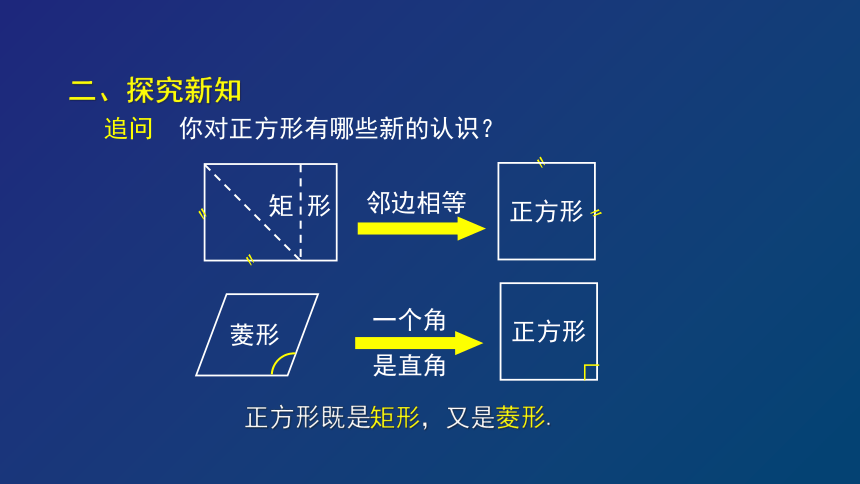
正方形既是矩形,又是菱形.
矩
形
追问
你对正方形有哪些新的认识?
二、探究新知
一组邻
边相等
平行
四边形
矩形
菱形
一个角
是直角
正方形
一个角
是直角
一组邻
边相等
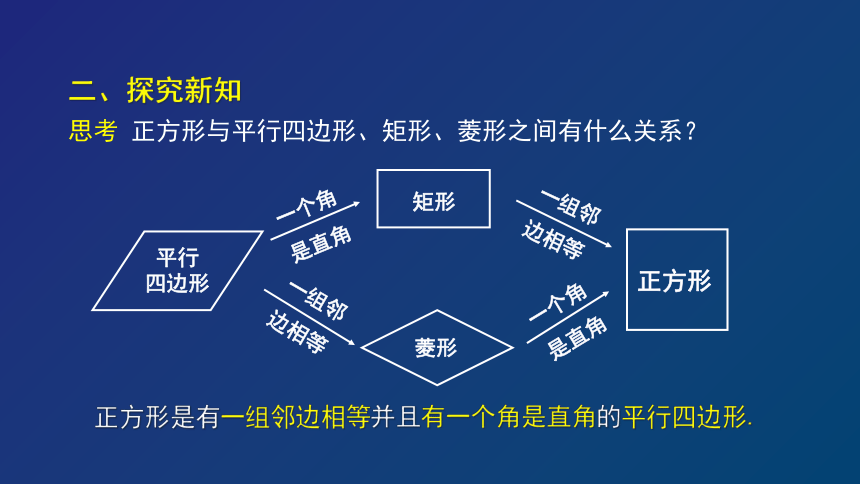
思考
正方形与平行四边形、矩形、菱形之间有什么关系?
正方形是有一组邻边相等并且有一个角是直角的平行四边形.
二、探究新知
矩形
菱形
正方形
平行四边形
思考
正方形与平行四边形、矩形、菱形之间有什么关系?
二、探究新知
平行四边形
矩形
菱形
性质
边
对边平行且相等
对边平行且相等
对边平行,四条边都相等
角
对角相等
四个角都是直角
对角相等
对角线
互相平分
相等且互相平分
互相垂直平分,
每一条对角线平分一组对角
思考
正方形有哪些性质?
正方形既有矩形的性质,又有菱形的性质.
二、探究新知
文字语言
图形
符号语言
边
角
∵四边形ABCD是正方形,
∴AB∥CD,AD∥BC,
AB=BC=CD=AD.
∵四边形ABCD
是正方形
,
∴∠A=∠B=
∠C=∠D=
90°.
正方形的性质
正方形的对边平行,四条边都相等.
正方形的四个角都是直角.
二、探究新知
文字语言
图形
符号语言
对
角
线
∵四边形ABCD是正方形
,
∴AC=BD,ACBD,
AO=OC,BO=OD
,
∠1=∠2,∠3=∠4
,
∠5=∠6,∠7=∠8.
正方形的性质
正方形的两条对角线相等,互相垂直平分,并且每一条对角线平分一组对角.
二、探究新知
问题5
?正方形是轴对称图形吗?如果是,它的对称轴有几条?分别是什么?
正方形是轴对称图形,它有4条对称轴,分别是对边中点的连线以及两条对角线所在的直线.
二、探究新知
思考
如何判定一个四边形是正方形?
一组邻边
相等
矩形
正方形
一个角是
直角
菱形
先判定一个四边形是矩形,再判定它是菱形
先判定一个四边形是菱形,再判定它是矩形
二、探究新知
1.有一组邻边相等并且有一个角是直角的平行四边形;
菱形
矩形
是正方形,
符合正方形的判定条件.
2.对角线互相垂直且相等的平行四边形.
问题6
满足下列条件的四边形是不是正方形?为什么?
2.对角线互相垂直且相等的平行四边形.
菱形
矩形
是正方形,符合正方形的判定条件.
2.对角线互相垂直且相等的平行四边形.
1.有一组邻边相等并且有一个角是直角的平行四边形;
二、探究新知
例
求证:
正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
已知:如图,四边形ABCD是正方形,对角线AC,BD相交于点O.
求证:△ABO,△BCO,△CDO,△DAO是全等的等腰直角三角形.
证明:∵
四边形ABCD是正方形,
∴
AC=BD,AC⊥BD,AO=BO=CO=DO.
∴
△ABO,△BCO,△CDO,△DAO都是等腰直角三角形,并且△ABO≌△BCO≌△CDO≌△DAO.
A
D
C
B
O
三、典型例题
〃
〃
〃
〃
A
D
C
B
O
图中共有多少个等腰直角三角形?
图中共有8个等腰直角三角形.
〃
〃
〃
〃
例
求证:
正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
已知:如图,四边形ABCD是正方形,对角线AC,BD相交于点O.
求证:△ABO,△BCO,△CDO,△DAO是全等的等腰直角三角形.
三、典型例题
四、课堂练习
1.如图,ABCD是一块正方形场地.
小华和小芳在AB边上取定了一点E,测量知,EC=30
m,EB=10
m.
这块场地的面积和对角线长分别是多少?
解:连接AC.
∴
∠ABC=90°,AB=BC.
在Rt△CBE中,EC=30,EB=10,
)
.
30
10
在Rt△ABC中,
.
答:这块场地的面积为,对角线长为.
30
10
四、课堂练习
1.如图,ABCD是一块正方形场地.
小华和小芳在AB边上取定了一点E,测量知,EC=30
m,EB=10
m.
这块场地的面积和对角线长分别是多少?
(1)对角线互相垂直的矩形;
(2)对角线相等的菱形;
(3)对角线互相垂直平分且相等的四边形.
是正方形,
是正方形,
是正方形,
2.
满足下列条件的四边形是不是正方形?为什么?
(3)对角线互相垂直平分且相等的四边形.
平行四边形
矩形
菱形
它符合正方形的判定条件.
它符合正方形的判定条件.
它符合正方形的判定条件.
四、课堂练习
3.
如图,E,F,M,N分别是正方形ABCD四条边上的点,且AE=BF=CM=DN.试判断四边形EFMN是什么图形,并证明你的结论.
E
F
N
M
A
D
C
B
〃
〃
〃
〃
理由如下:∵
四边形ABCD是正方形,
∴
AB=BC=CD=DA,∠A=∠B=∠C=∠D=90°.
∵
AE=BF=CM=DN
,
∴
AN=BE=CF=DM.
∴
△AEN≌△BFE≌△CMF≌△DNM.
?
?
?
?
解:四边形EFMN是正方形.
四、课堂练习
∴
NE=EF=FM=MN,∠AEN
=∠BFE.
∴四边形EFMN是菱形.
在Rt△EBF中,∠BFE+∠BEF
=
90°,
∴∠AEN
+∠BEF
=
90°,
∴∠NEF
=
90°.
∴四边形EFMN是正方形.
E
F
N
M
A
D
C
B
〃
〃
〃
〃
?
?
?
?
四、课堂练习
3.
如图,E,F,M,N分别是正方形ABCD四条边上的点,且AE=BF=CM=DN.试判断四边形EFMN是什么图形,并证明你的结论.
先判定一个四边形是矩形,再判定它是菱形
先判定一个四边形是菱形,再判定它是矩形
边
角
正方形
性质
定义
判定
对角线
1.
本节课我们学习了哪些内容?
五、课堂小结
图形的对称性
对边平行,四条边都相等
四个角都是直角
轴对称图形
相等且互相垂直平分,
每一条对角线平分一组对角
2.正方形与平行四边形、矩形、菱形之间有什么关系?
五、课堂小结
矩形
菱形
正方形
平行四边形
五、课堂小结
2.正方形与平行四边形、矩形、菱形之间有什么关系?
六、布置作业
教科书第59页练习1,
教科书第62页第15题.
谢谢观看!
18.2.3
正方形
八年级
数学
学习目标:
1.理解正方形的概念,以及与平行四边形、矩形、菱形之间的关系.
2.探索正方形的性质定理和判定定理,并能运用它们进行证明和计算.
一组邻
边相等
平行
四边形
矩形
菱形
一个角
是直角
一、复习引入
两组对边分别平行的四边形叫做平行四边形.
问题1(1)我们已经学习了哪些特殊的四边形?它们是如何定义的?
有一个角是直角的平行四边形叫做矩形.
有一组邻边相等的平行四边形叫做菱形.
问题1(2)我们是如何研究这些图形的?
定义
性质
边
角
对角线
判定
一、复习引入
问题2
在小学,我们还学习过什么特殊的平行四边形?
正方形
正方形的四条边都相等,四个角都是直角.
一、复习引入
问题3
你能用一张矩形纸片,折出一个最大的正方形吗?请说说你的方法.
二、探究新知
问题4
菱形具有怎样的条件才能是正方形呢?
正方形
二、探究新知
邻边相等
〃
〃
〃
正方形
〃
菱形
一个角
是直角
正方形
∟
正方形既是矩形,又是菱形.
矩
形
追问
你对正方形有哪些新的认识?
二、探究新知
一组邻
边相等
平行
四边形
矩形
菱形
一个角
是直角
正方形
一个角
是直角
一组邻
边相等
思考
正方形与平行四边形、矩形、菱形之间有什么关系?
正方形是有一组邻边相等并且有一个角是直角的平行四边形.
二、探究新知
矩形
菱形
正方形
平行四边形
思考
正方形与平行四边形、矩形、菱形之间有什么关系?
二、探究新知
平行四边形
矩形
菱形
性质
边
对边平行且相等
对边平行且相等
对边平行,四条边都相等
角
对角相等
四个角都是直角
对角相等
对角线
互相平分
相等且互相平分
互相垂直平分,
每一条对角线平分一组对角
思考
正方形有哪些性质?
正方形既有矩形的性质,又有菱形的性质.
二、探究新知
文字语言
图形
符号语言
边
角
∵四边形ABCD是正方形,
∴AB∥CD,AD∥BC,
AB=BC=CD=AD.
∵四边形ABCD
是正方形
,
∴∠A=∠B=
∠C=∠D=
90°.
正方形的性质
正方形的对边平行,四条边都相等.
正方形的四个角都是直角.
二、探究新知
文字语言
图形
符号语言
对
角
线
∵四边形ABCD是正方形
,
∴AC=BD,ACBD,
AO=OC,BO=OD
,
∠1=∠2,∠3=∠4
,
∠5=∠6,∠7=∠8.
正方形的性质
正方形的两条对角线相等,互相垂直平分,并且每一条对角线平分一组对角.
二、探究新知
问题5
?正方形是轴对称图形吗?如果是,它的对称轴有几条?分别是什么?
正方形是轴对称图形,它有4条对称轴,分别是对边中点的连线以及两条对角线所在的直线.
二、探究新知
思考
如何判定一个四边形是正方形?
一组邻边
相等
矩形
正方形
一个角是
直角
菱形
先判定一个四边形是矩形,再判定它是菱形
先判定一个四边形是菱形,再判定它是矩形
二、探究新知
1.有一组邻边相等并且有一个角是直角的平行四边形;
菱形
矩形
是正方形,
符合正方形的判定条件.
2.对角线互相垂直且相等的平行四边形.
问题6
满足下列条件的四边形是不是正方形?为什么?
2.对角线互相垂直且相等的平行四边形.
菱形
矩形
是正方形,符合正方形的判定条件.
2.对角线互相垂直且相等的平行四边形.
1.有一组邻边相等并且有一个角是直角的平行四边形;
二、探究新知
例
求证:
正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
已知:如图,四边形ABCD是正方形,对角线AC,BD相交于点O.
求证:△ABO,△BCO,△CDO,△DAO是全等的等腰直角三角形.
证明:∵
四边形ABCD是正方形,
∴
AC=BD,AC⊥BD,AO=BO=CO=DO.
∴
△ABO,△BCO,△CDO,△DAO都是等腰直角三角形,并且△ABO≌△BCO≌△CDO≌△DAO.
A
D
C
B
O
三、典型例题
〃
〃
〃
〃
A
D
C
B
O
图中共有多少个等腰直角三角形?
图中共有8个等腰直角三角形.
〃
〃
〃
〃
例
求证:
正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
已知:如图,四边形ABCD是正方形,对角线AC,BD相交于点O.
求证:△ABO,△BCO,△CDO,△DAO是全等的等腰直角三角形.
三、典型例题
四、课堂练习
1.如图,ABCD是一块正方形场地.
小华和小芳在AB边上取定了一点E,测量知,EC=30
m,EB=10
m.
这块场地的面积和对角线长分别是多少?
解:连接AC.
∴
∠ABC=90°,AB=BC.
在Rt△CBE中,EC=30,EB=10,
)
.
30
10
在Rt△ABC中,
.
答:这块场地的面积为,对角线长为.
30
10
四、课堂练习
1.如图,ABCD是一块正方形场地.
小华和小芳在AB边上取定了一点E,测量知,EC=30
m,EB=10
m.
这块场地的面积和对角线长分别是多少?
(1)对角线互相垂直的矩形;
(2)对角线相等的菱形;
(3)对角线互相垂直平分且相等的四边形.
是正方形,
是正方形,
是正方形,
2.
满足下列条件的四边形是不是正方形?为什么?
(3)对角线互相垂直平分且相等的四边形.
平行四边形
矩形
菱形
它符合正方形的判定条件.
它符合正方形的判定条件.
它符合正方形的判定条件.
四、课堂练习
3.
如图,E,F,M,N分别是正方形ABCD四条边上的点,且AE=BF=CM=DN.试判断四边形EFMN是什么图形,并证明你的结论.
E
F
N
M
A
D
C
B
〃
〃
〃
〃
理由如下:∵
四边形ABCD是正方形,
∴
AB=BC=CD=DA,∠A=∠B=∠C=∠D=90°.
∵
AE=BF=CM=DN
,
∴
AN=BE=CF=DM.
∴
△AEN≌△BFE≌△CMF≌△DNM.
?
?
?
?
解:四边形EFMN是正方形.
四、课堂练习
∴
NE=EF=FM=MN,∠AEN
=∠BFE.
∴四边形EFMN是菱形.
在Rt△EBF中,∠BFE+∠BEF
=
90°,
∴∠AEN
+∠BEF
=
90°,
∴∠NEF
=
90°.
∴四边形EFMN是正方形.
E
F
N
M
A
D
C
B
〃
〃
〃
〃
?
?
?
?
四、课堂练习
3.
如图,E,F,M,N分别是正方形ABCD四条边上的点,且AE=BF=CM=DN.试判断四边形EFMN是什么图形,并证明你的结论.
先判定一个四边形是矩形,再判定它是菱形
先判定一个四边形是菱形,再判定它是矩形
边
角
正方形
性质
定义
判定
对角线
1.
本节课我们学习了哪些内容?
五、课堂小结
图形的对称性
对边平行,四条边都相等
四个角都是直角
轴对称图形
相等且互相垂直平分,
每一条对角线平分一组对角
2.正方形与平行四边形、矩形、菱形之间有什么关系?
五、课堂小结
矩形
菱形
正方形
平行四边形
五、课堂小结
2.正方形与平行四边形、矩形、菱形之间有什么关系?
六、布置作业
教科书第59页练习1,
教科书第62页第15题.
谢谢观看!
