天津市2020年空中课堂人教版八年级数学下册19.2.2 一次函数课件(共32张PPT)
文档属性
| 名称 | 天津市2020年空中课堂人教版八年级数学下册19.2.2 一次函数课件(共32张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 7.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-26 00:00:00 | ||
图片预览










文档简介
(共32张PPT)
19.2.2
一次函数
学习目标
1.结合具体情境体会一次函数的意义,能根据已知条件确定一次函数的表达式.
2.
能画出一次函数的图象,根据一次函数的图象和表达式
探索并理解
k>0和
k<0时,图象的变化情况.
3.
会利用待定系数法确定一次函数的表达式.
4.
能用一次函数解决简单的实际问题.
一、创设情境,引入新知
问题2
某登山队大本营所在地的气温为5
℃,海拔每升高1
km气温下降6
℃.登山队员由大本营向上登高
x
km时,他们所在位置的气温是y
℃.试用函数解析式表示
y
与
x
的关系.
思考 下列问题中,变量之间的对应关系是函数关系吗?如果是,请写出函数解析式.
(1)有人发现,在20
℃~25
℃时蟋蟀每分鸣叫次数
c
与温度
t(单位:℃)有关,即
c
的值约是
t
的7
倍与35的差.
(2)一种计算成年人标准体重G(单位:kg)的方法是:以厘米为单位量出身高值
h
,再减常数105,所得差是G
的值.
c与t是函数关系
G与h是函数关系
二、分析问题,探求新知
(3)某城市的市内电话的月收费额
y(单位:元)包括月
租费22元和拨打电话
x
min
的计时费(按0.1元/min收取).
(4)把一个长10
cm、宽5
cm的长方形的长减少
x
cm,宽不
变,长方形的面积
y(单位:cm2)随
x
的变化而变化.
(0≤x<
10)
y与x是函数关系
y与x是函数关系
二、分析问题,探求新知
(1)
(2)
(3)
(4)
观察以下的四个函数解析式,很显然它们不是正比例函数,这些函数解析式有哪些共同特征?
这些函数都是常数
k
与自变量的积与常数
b
的和的形式.
思考
函数
自变量的系数
自变量
常数
c
7
t
-35
G
1
h
-105
y
0.1
x
22
y
-5
x
50
思考:一次函数y=kx+b与正比例函数有什么关系呢?
一般地,形如y=kx+b(k,b是常数,k≠0)的函数,叫做一次函数.
特别注意:
k
≠
0,自变量x的指数是“1”.
定义
当b=0时,y=kx+b就变成了y=kx,所以说正比例函数是一种特殊的一次函数.
下列函数中哪些是一次函数,哪些又是正比例函数?
练习
(1)
(2)
(3)
(4)
类比研究
问题1:类比正比例函数的研究过程,我们接着要研究一次
函数的哪些方面呢?
图象(形状,位置,变化趋势)和性质(增减性).
问题2:我们是如何研究的呢?
过点
画函数
的图象.
16
14
12
10
8
6
4
2
-2
-4
-6
-8
12
6
0
-6
-12
17
11
5
-1
-7
-2
o
2
x
-2
-1
0
1
2
y
x
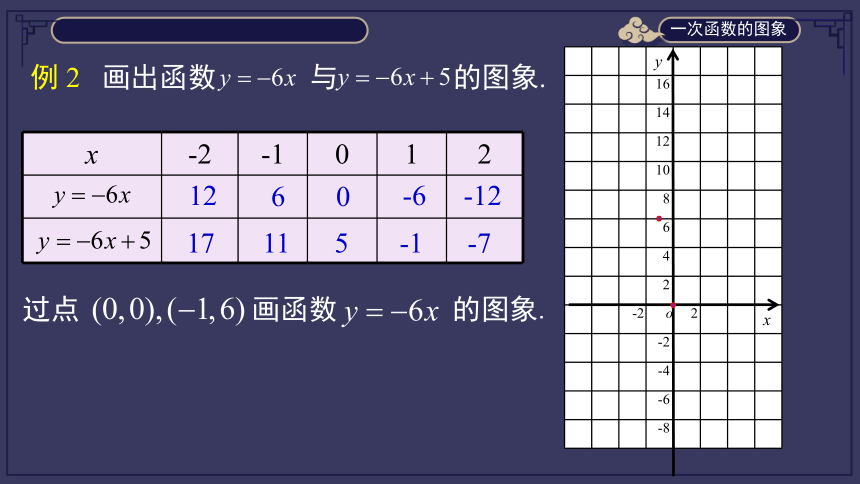
例
2
画出函数
与
的图象.
12
6
0
-6
-12
17
11
5
-1
-7
描点
16
14
12
10
8
6
4
2
-2
-4
-6
-8
-2
o
2
过点
画函数
的图象.
y
x
x
-2
-1
0
1
2
16
14
12
10
8
6
4
2
-2
-4
-6
-8
12
6
0
-6
-12
17
11
5
-1
-7
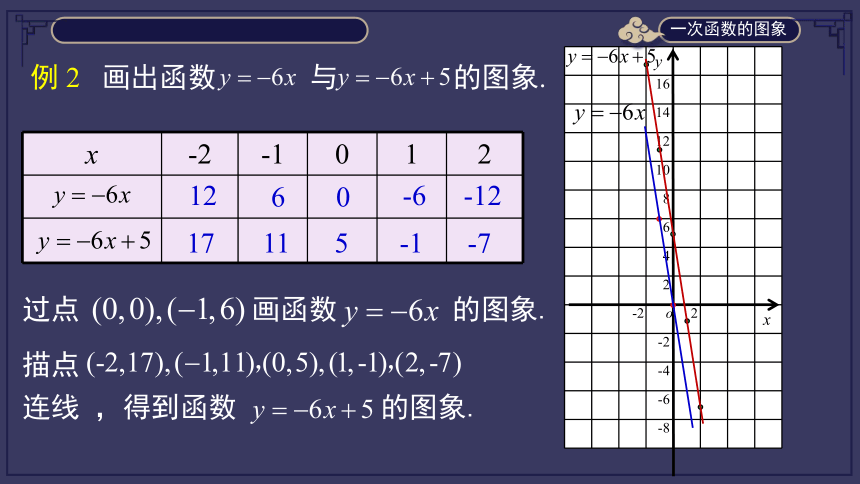
例
2
画出函数
与
的图象.
过点
画函数
的图象.
描点
-2
o
2
连线
,得到函数
的图象.
y
x
x
-2
-1
0
1
2
-2
o
2
12
6
0
-6
-12
17
11
5
-1
-7
思考:函数
的图象是什么?
追问:为什么说画出来的图象是一条直线呢?
16
14
12
10
8
6
4
2
-2
-4
-6
-8
对自变量的任意数值,这两个函数相应的值总差同一个常数5.
例
2
画出函数
与
的图象.
y
x
x
-2
-1
0
1
2
16
14
12
10
8
6
4
2
-2
-4
-6
-8
-2
o
2
12
6
0
-6
-12
17
11
5
-1
-7
对自变量的任意数值,这两个函数相应的值总差同一个常数5.
的图象向上平
移5个单位长度得到
的图象.
思考:函数
的图象是什么?
追问:为什么说画出来的图象是一条直线呢?
例
2
画出函数
与
的图象.
y
x
x
-2
-1
0
1
2
-2
o
2
16
14
12
10
8
6
4
2
-2
-4
-6
-8
观察与比较
比较上面两个函数图象的相同点
与不同点,填出你的观察结果:
这两个函数的图象形状都是
,并且倾斜程度
.函数
的图象经过原点,函数
的图象与y轴交于点
,即它可以看作由直线
向
平移
个单位长度得到.
直线
相同
上
5
(0,5)
y
x
-2
o
2
观察与比较
这两个函数的图象形状都是
,并且倾斜程度
.函数
的图象经过原点,函数
的图象与y轴交于点
,即它可以看作由直线
向
平移
个单位长度得到.
比较上面两个函数图象的相同点
与不同点,填出你的观察结果:
直线
相同
上
5
16
14
12
10
8
6
4
2
-2
-4
-6
-8
(0,5)
y
x
总结归纳
一次函数
的图象可以由直线y=kx平移︱b︱个单位长度得到(当b>0时,向上平移;
当b<0时,向下平移).一次函数
的图象也是一条直线,我们称它为直线
y=kx+b.
画出函数
与
的图象.
解:列表表示当
,
时两个函数的对应值.
过点(0,-1)与点(1,1)画直线
;
-1
1
1
0.5
例3
x
0
1
思考:你有画一次函数图象的简便方法吗?
过点(0,
1)与点(1,0.5)画直线
探究
画出函数
,
的图象.
1
2
1
3
1
0
1
-1
画出函数
,
的图象.
当自变量x=0时函数值都等于1,所以四条直线都过点(0,1).
x
0
1
x
0
1
思考
当k>0时,直线y=kx+b从左向右上升;当k<0时,直线y=kx+b从左向右下降.
你能看出k
的正负对图象有什么影响吗?
追问:你能进一步说出函数值怎样随着自变量
x
的变化而变
化吗?
结论
当k>0时,y随x的增大而______;
当k<0时,y随x的增大而______.
增大
减小
一次函数y=kx+b
(k,b是常数,k
≠
0)具有如下性质:
直线
与x轴交点的坐标为
,与y轴交点的坐标为
,图象经过
象限,y随x的增大而
.
练习
(1.5
,0)
(0,-3)
一、三、四
增大
已知一次函数的图象经过点(3,5)与(-4,-9),求这个一次函数的解析式.
例4
分析:
求一次函数
的解析式,关键是求出
k,b
的值,从已知条件可以列出关于
k,b
的二元一次方程组,并求出
k,b.
例4
解:设这个一次函数的解析式为
.
因为
y=kx+b的图象过点(3,5)与(-4,-9),所以
解方程组得
这个一次函数的解析式为
.
待定系数法.
归纳
从数到形
从形到数
函数解析式
y=kx+b
满足条件的两定点(x1,y1)与(x2,y2)
一次函数的图象直线l
选取
画出
解出
选取
数形结合
“黄金1号”玉米种子的价格为
5
元/kg.
如果一次购买
2
kg
以上的种子,超过
2
kg部分的种子价格打
8
折.
(1)填出下表:
5×购买量
5×2+超过2kg的部分×4
例如:购买量是2.5
kg时,付款金额为
例5
2.5
5
7.5
10
12
14
16
18
购买量/kg
0.5
1
1.5
2
2.5
3
3.5
4
…
付款金额/元
…
例5
分析:付款金额与种子价格相关,问题中种子价格不是固定不变的,它与购买量有关,写函数解析式与画函数图象时,应对购买量
x
进行当0≤x≤2
和x>2
时分段讨论.
“黄金1号”玉米种子的价格为
5
元/kg.
如果一次购买
2
kg
以上的种子,超过
2
kg部分的种子价格打
8
折.
(2)写出付款金额关于购买量的函数解析式,并画出函
数图象.
“黄金1号”玉米种子的价格为
5
元/kg.
如果一次购买
2
kg
以上的种子,超过
2
kg部分的种子价格打
8
折.
(2)写出付款金额关于购买量的函数解析式,并画出函
数图象.
解:设购买量为x
kg,付款金额为y
元.
当0
≤x≤2时,y=5x;
当x
>2时,
.
例5
思考:你能由上面的解析式解决以下问题吗?
(1)一次购买1.5
kg种子,需付款多少元?
(2)一次购买3
kg
种子,需付款多少元?
例5
y=kx+b(k,b是常数,k≠0)
解析式
图象
直线
性质
y=kx
(k≠0)的图象平移或两点法
当k>0时,y随x的增大而增大;
当k<0时,y随x的增大而减小.
待定系数法
数形结合、类比、归纳概括
三、小结归纳,拓展深化
教材第99页,第3、10、11题.
四、布置作业,提高升华
19.2.2
一次函数
学习目标
1.结合具体情境体会一次函数的意义,能根据已知条件确定一次函数的表达式.
2.
能画出一次函数的图象,根据一次函数的图象和表达式
探索并理解
k>0和
k<0时,图象的变化情况.
3.
会利用待定系数法确定一次函数的表达式.
4.
能用一次函数解决简单的实际问题.
一、创设情境,引入新知
问题2
某登山队大本营所在地的气温为5
℃,海拔每升高1
km气温下降6
℃.登山队员由大本营向上登高
x
km时,他们所在位置的气温是y
℃.试用函数解析式表示
y
与
x
的关系.
思考 下列问题中,变量之间的对应关系是函数关系吗?如果是,请写出函数解析式.
(1)有人发现,在20
℃~25
℃时蟋蟀每分鸣叫次数
c
与温度
t(单位:℃)有关,即
c
的值约是
t
的7
倍与35的差.
(2)一种计算成年人标准体重G(单位:kg)的方法是:以厘米为单位量出身高值
h
,再减常数105,所得差是G
的值.
c与t是函数关系
G与h是函数关系
二、分析问题,探求新知
(3)某城市的市内电话的月收费额
y(单位:元)包括月
租费22元和拨打电话
x
min
的计时费(按0.1元/min收取).
(4)把一个长10
cm、宽5
cm的长方形的长减少
x
cm,宽不
变,长方形的面积
y(单位:cm2)随
x
的变化而变化.
(0≤x<
10)
y与x是函数关系
y与x是函数关系
二、分析问题,探求新知
(1)
(2)
(3)
(4)
观察以下的四个函数解析式,很显然它们不是正比例函数,这些函数解析式有哪些共同特征?
这些函数都是常数
k
与自变量的积与常数
b
的和的形式.
思考
函数
自变量的系数
自变量
常数
c
7
t
-35
G
1
h
-105
y
0.1
x
22
y
-5
x
50
思考:一次函数y=kx+b与正比例函数有什么关系呢?
一般地,形如y=kx+b(k,b是常数,k≠0)的函数,叫做一次函数.
特别注意:
k
≠
0,自变量x的指数是“1”.
定义
当b=0时,y=kx+b就变成了y=kx,所以说正比例函数是一种特殊的一次函数.
下列函数中哪些是一次函数,哪些又是正比例函数?
练习
(1)
(2)
(3)
(4)
类比研究
问题1:类比正比例函数的研究过程,我们接着要研究一次
函数的哪些方面呢?
图象(形状,位置,变化趋势)和性质(增减性).
问题2:我们是如何研究的呢?
过点
画函数
的图象.
16
14
12
10
8
6
4
2
-2
-4
-6
-8
12
6
0
-6
-12
17
11
5
-1
-7
-2
o
2
x
-2
-1
0
1
2
y
x
例
2
画出函数
与
的图象.
12
6
0
-6
-12
17
11
5
-1
-7
描点
16
14
12
10
8
6
4
2
-2
-4
-6
-8
-2
o
2
过点
画函数
的图象.
y
x
x
-2
-1
0
1
2
16
14
12
10
8
6
4
2
-2
-4
-6
-8
12
6
0
-6
-12
17
11
5
-1
-7
例
2
画出函数
与
的图象.
过点
画函数
的图象.
描点
-2
o
2
连线
,得到函数
的图象.
y
x
x
-2
-1
0
1
2
-2
o
2
12
6
0
-6
-12
17
11
5
-1
-7
思考:函数
的图象是什么?
追问:为什么说画出来的图象是一条直线呢?
16
14
12
10
8
6
4
2
-2
-4
-6
-8
对自变量的任意数值,这两个函数相应的值总差同一个常数5.
例
2
画出函数
与
的图象.
y
x
x
-2
-1
0
1
2
16
14
12
10
8
6
4
2
-2
-4
-6
-8
-2
o
2
12
6
0
-6
-12
17
11
5
-1
-7
对自变量的任意数值,这两个函数相应的值总差同一个常数5.
的图象向上平
移5个单位长度得到
的图象.
思考:函数
的图象是什么?
追问:为什么说画出来的图象是一条直线呢?
例
2
画出函数
与
的图象.
y
x
x
-2
-1
0
1
2
-2
o
2
16
14
12
10
8
6
4
2
-2
-4
-6
-8
观察与比较
比较上面两个函数图象的相同点
与不同点,填出你的观察结果:
这两个函数的图象形状都是
,并且倾斜程度
.函数
的图象经过原点,函数
的图象与y轴交于点
,即它可以看作由直线
向
平移
个单位长度得到.
直线
相同
上
5
(0,5)
y
x
-2
o
2
观察与比较
这两个函数的图象形状都是
,并且倾斜程度
.函数
的图象经过原点,函数
的图象与y轴交于点
,即它可以看作由直线
向
平移
个单位长度得到.
比较上面两个函数图象的相同点
与不同点,填出你的观察结果:
直线
相同
上
5
16
14
12
10
8
6
4
2
-2
-4
-6
-8
(0,5)
y
x
总结归纳
一次函数
的图象可以由直线y=kx平移︱b︱个单位长度得到(当b>0时,向上平移;
当b<0时,向下平移).一次函数
的图象也是一条直线,我们称它为直线
y=kx+b.
画出函数
与
的图象.
解:列表表示当
,
时两个函数的对应值.
过点(0,-1)与点(1,1)画直线
;
-1
1
1
0.5
例3
x
0
1
思考:你有画一次函数图象的简便方法吗?
过点(0,
1)与点(1,0.5)画直线
探究
画出函数
,
的图象.
1
2
1
3
1
0
1
-1
画出函数
,
的图象.
当自变量x=0时函数值都等于1,所以四条直线都过点(0,1).
x
0
1
x
0
1
思考
当k>0时,直线y=kx+b从左向右上升;当k<0时,直线y=kx+b从左向右下降.
你能看出k
的正负对图象有什么影响吗?
追问:你能进一步说出函数值怎样随着自变量
x
的变化而变
化吗?
结论
当k>0时,y随x的增大而______;
当k<0时,y随x的增大而______.
增大
减小
一次函数y=kx+b
(k,b是常数,k
≠
0)具有如下性质:
直线
与x轴交点的坐标为
,与y轴交点的坐标为
,图象经过
象限,y随x的增大而
.
练习
(1.5
,0)
(0,-3)
一、三、四
增大
已知一次函数的图象经过点(3,5)与(-4,-9),求这个一次函数的解析式.
例4
分析:
求一次函数
的解析式,关键是求出
k,b
的值,从已知条件可以列出关于
k,b
的二元一次方程组,并求出
k,b.
例4
解:设这个一次函数的解析式为
.
因为
y=kx+b的图象过点(3,5)与(-4,-9),所以
解方程组得
这个一次函数的解析式为
.
待定系数法.
归纳
从数到形
从形到数
函数解析式
y=kx+b
满足条件的两定点(x1,y1)与(x2,y2)
一次函数的图象直线l
选取
画出
解出
选取
数形结合
“黄金1号”玉米种子的价格为
5
元/kg.
如果一次购买
2
kg
以上的种子,超过
2
kg部分的种子价格打
8
折.
(1)填出下表:
5×购买量
5×2+超过2kg的部分×4
例如:购买量是2.5
kg时,付款金额为
例5
2.5
5
7.5
10
12
14
16
18
购买量/kg
0.5
1
1.5
2
2.5
3
3.5
4
…
付款金额/元
…
例5
分析:付款金额与种子价格相关,问题中种子价格不是固定不变的,它与购买量有关,写函数解析式与画函数图象时,应对购买量
x
进行当0≤x≤2
和x>2
时分段讨论.
“黄金1号”玉米种子的价格为
5
元/kg.
如果一次购买
2
kg
以上的种子,超过
2
kg部分的种子价格打
8
折.
(2)写出付款金额关于购买量的函数解析式,并画出函
数图象.
“黄金1号”玉米种子的价格为
5
元/kg.
如果一次购买
2
kg
以上的种子,超过
2
kg部分的种子价格打
8
折.
(2)写出付款金额关于购买量的函数解析式,并画出函
数图象.
解:设购买量为x
kg,付款金额为y
元.
当0
≤x≤2时,y=5x;
当x
>2时,
.
例5
思考:你能由上面的解析式解决以下问题吗?
(1)一次购买1.5
kg种子,需付款多少元?
(2)一次购买3
kg
种子,需付款多少元?
例5
y=kx+b(k,b是常数,k≠0)
解析式
图象
直线
性质
y=kx
(k≠0)的图象平移或两点法
当k>0时,y随x的增大而增大;
当k<0时,y随x的增大而减小.
待定系数法
数形结合、类比、归纳概括
三、小结归纳,拓展深化
教材第99页,第3、10、11题.
四、布置作业,提高升华
