人教版九年级下册数学 27.2.1 相似三角形的判定 (第1课时 共15张PPT)
文档属性
| 名称 | 人教版九年级下册数学 27.2.1 相似三角形的判定 (第1课时 共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 347.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-27 08:31:35 | ||
图片预览




文档简介
(共15张PPT)
27.2.1 相似三角形的判定
(第一课时)
人教版
九年级 下册
什么是相似多边形?它具有什么性质?
两个边数相同的多边形,如果它们的角分别
,边
,那么这两个多边形叫做相似多边形.
相等
成比例
相似多边形的对应角相等,对应边成比例。
温故而知新
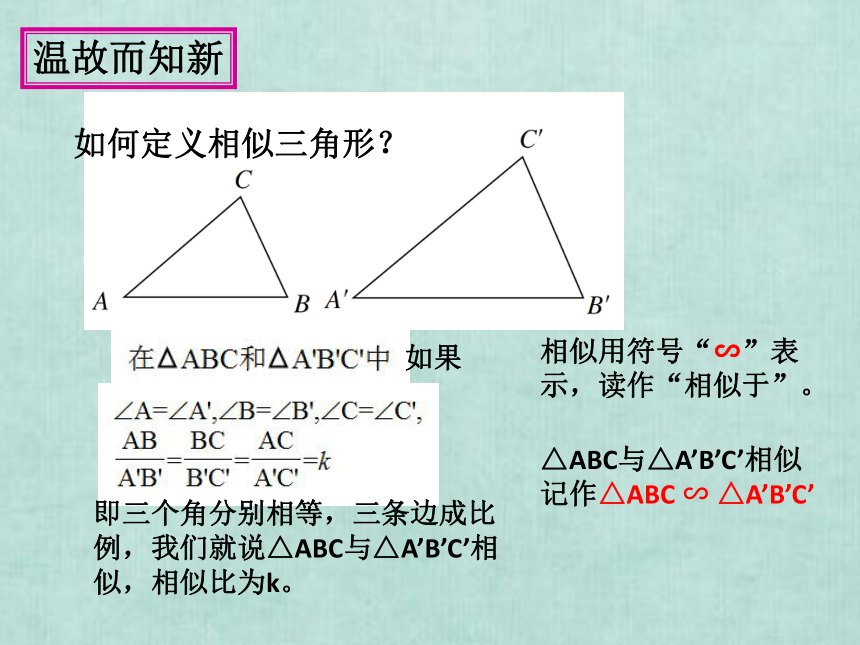
如何定义相似三角形?
如果
即三个角分别相等,三条边成比例,我们就说△ABC与△A’B’C’相似,相似比为k。
相似用符号“∽”表示,读作“相似于”。
△ABC与△A’B’C’相似记作△ABC
∽
△A’B’C’
温故而知新
温故而知新
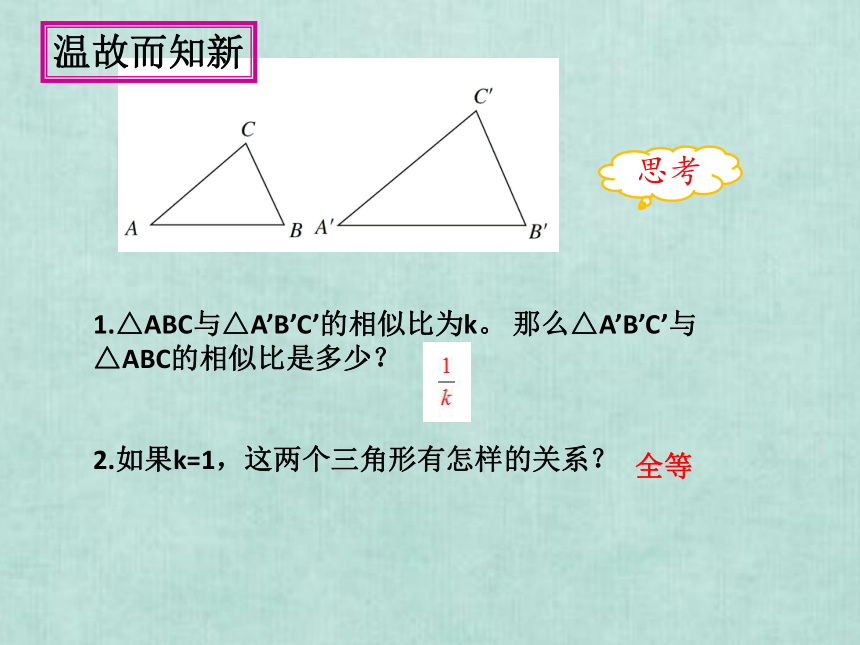
2.如果k=1,这两个三角形有怎样的关系?
思考
1.△ABC与△A’B’C’的相似比为k。
那么△A’B’C’与△ABC的相似比是多少?
全等
学习三角形全等时,我们知道,除了可以验证所有的角和边分别相等来判定两个三角形全等外,还有判定的简便方法(SSS,SAS,ASA,AAS).类似地,判定两个三角形相似时,是不是也存在简便的判定方法呢?
类比猜想,探索新知
问题 如图,任意画两条直线l1,l2
,再画三条与l1,l2都相交的平行线l3,l4,l5
.分别度量l3,l4,l5在
l1,l2
上截得的两条线段AB,BC和在l2上截得的两条线段DE,EF的
长度,
相等吗?任意平移
l5,
还相等吗?
问题探究,发现事实
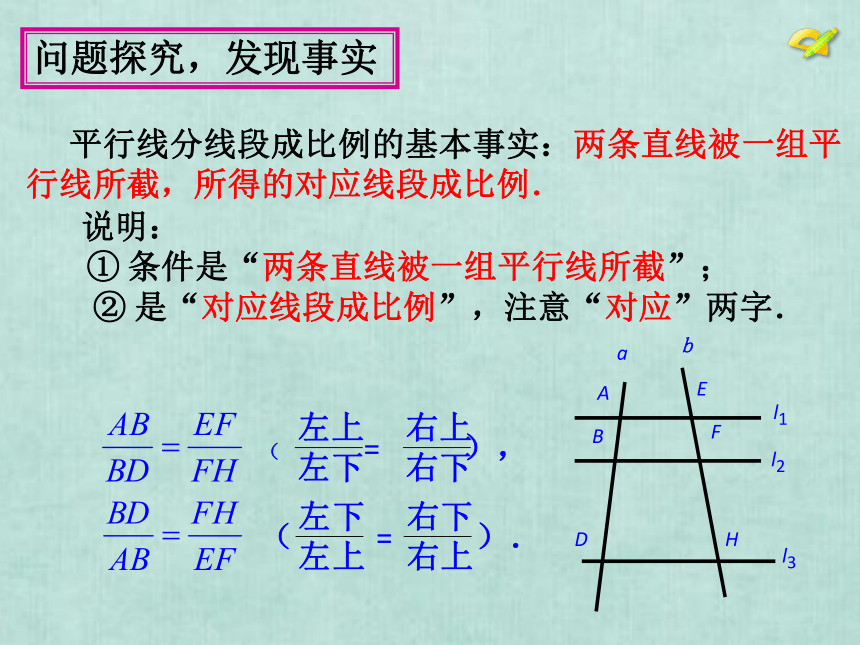
平行线分线段成比例的基本事实:两条直线被一组平行线所截,所得的对应线段成比例.
说明:
①
条件是“两条直线被一组平行线所截”;
②
是“对应线段成比例”,注意“对应”两字.
l3
l1
l2
A
B
D
E
F
H
a
b
(
=
),
左上
左下
右上
右下
(
=
).
左下
左上
右下
右上
问题探究,发现事实
练习:如图AB//CD//EF,AF与BE相交于点G,AG=2,GD=1,DF=5,求
的值.
结论:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
把基本事实应用到三角形中:
D
E
A
B
A
l3
l1
l2
C
l3
l1
l2
B
D
E
C
l5
l4
l4
l5
观察猜想,提出问题
∵ l3∥l4
∥l5
.
∴
,
,
等.
CE
AE
BD
AD
=
如图,在△ABC
中,DE∥BC,且
DE
分别交
AB,
AC
于点
D,E,△ADE
与△ABC
有什么关系?
观察猜想,提出问题
A
l3
l1
l2
B
D
E
C
l5
l4
A
B
C
D
E
用定义证明△ADE∽△ABC,
需要具备的条件:
角:∠A=∠A,∠ADE=∠B,∠AED=∠C;
A
B
C
D
E
边: .
合作交流,探究定理
1.如图,在△ABC
中,DE∥BC,且
AD=3,
DB=2,指出图中的相似三角形,并求出其相似比.
学以致用,巩固新知
A
B
C
D
E
2.如图,在△ABC
中,DE∥BC,且
AD=8,DB=
12,AC=15,DE=7,求
AE
和
BC
的长.
学以致用,巩固新知
A
D
E
B
C
1.本节课我们学习了三角形相似的哪种判定方法?这种判定方法的前提条件是什么?
2.我们是如何证明判定定理的?
反思与小结
平行线分线段成
比例的基本事实
应用到三角形中
结
论
以结论为基础
判定三角形
相似的定理
1.教科书习题
27.2 第
4,5
题.
布置作业
27.2.1 相似三角形的判定
(第一课时)
人教版
九年级 下册
什么是相似多边形?它具有什么性质?
两个边数相同的多边形,如果它们的角分别
,边
,那么这两个多边形叫做相似多边形.
相等
成比例
相似多边形的对应角相等,对应边成比例。
温故而知新
如何定义相似三角形?
如果
即三个角分别相等,三条边成比例,我们就说△ABC与△A’B’C’相似,相似比为k。
相似用符号“∽”表示,读作“相似于”。
△ABC与△A’B’C’相似记作△ABC
∽
△A’B’C’
温故而知新
温故而知新
2.如果k=1,这两个三角形有怎样的关系?
思考
1.△ABC与△A’B’C’的相似比为k。
那么△A’B’C’与△ABC的相似比是多少?
全等
学习三角形全等时,我们知道,除了可以验证所有的角和边分别相等来判定两个三角形全等外,还有判定的简便方法(SSS,SAS,ASA,AAS).类似地,判定两个三角形相似时,是不是也存在简便的判定方法呢?
类比猜想,探索新知
问题 如图,任意画两条直线l1,l2
,再画三条与l1,l2都相交的平行线l3,l4,l5
.分别度量l3,l4,l5在
l1,l2
上截得的两条线段AB,BC和在l2上截得的两条线段DE,EF的
长度,
相等吗?任意平移
l5,
还相等吗?
问题探究,发现事实
平行线分线段成比例的基本事实:两条直线被一组平行线所截,所得的对应线段成比例.
说明:
①
条件是“两条直线被一组平行线所截”;
②
是“对应线段成比例”,注意“对应”两字.
l3
l1
l2
A
B
D
E
F
H
a
b
(
=
),
左上
左下
右上
右下
(
=
).
左下
左上
右下
右上
问题探究,发现事实
练习:如图AB//CD//EF,AF与BE相交于点G,AG=2,GD=1,DF=5,求
的值.
结论:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
把基本事实应用到三角形中:
D
E
A
B
A
l3
l1
l2
C
l3
l1
l2
B
D
E
C
l5
l4
l4
l5
观察猜想,提出问题
∵ l3∥l4
∥l5
.
∴
,
,
等.
CE
AE
BD
AD
=
如图,在△ABC
中,DE∥BC,且
DE
分别交
AB,
AC
于点
D,E,△ADE
与△ABC
有什么关系?
观察猜想,提出问题
A
l3
l1
l2
B
D
E
C
l5
l4
A
B
C
D
E
用定义证明△ADE∽△ABC,
需要具备的条件:
角:∠A=∠A,∠ADE=∠B,∠AED=∠C;
A
B
C
D
E
边: .
合作交流,探究定理
1.如图,在△ABC
中,DE∥BC,且
AD=3,
DB=2,指出图中的相似三角形,并求出其相似比.
学以致用,巩固新知
A
B
C
D
E
2.如图,在△ABC
中,DE∥BC,且
AD=8,DB=
12,AC=15,DE=7,求
AE
和
BC
的长.
学以致用,巩固新知
A
D
E
B
C
1.本节课我们学习了三角形相似的哪种判定方法?这种判定方法的前提条件是什么?
2.我们是如何证明判定定理的?
反思与小结
平行线分线段成
比例的基本事实
应用到三角形中
结
论
以结论为基础
判定三角形
相似的定理
1.教科书习题
27.2 第
4,5
题.
布置作业
