湘教版九年级数学下册 第1章 二次函数 单元测试(3)(含答案)
文档属性
| 名称 | 湘教版九年级数学下册 第1章 二次函数 单元测试(3)(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 244.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-25 21:26:18 | ||
图片预览



文档简介
第1章
二次函数
单元测试(3)
1、选择题
1.已知二次函数y=2x2-3,当-1≤x≤2时,y的取值范围是( )
A.-1≤y≤5
B.-5≤y≤5
C.-3≤y≤5
D.-2≤y≤1
2.当二次函数y=x2+4x+9取最小值时,x的值为( )
A.-2
B.1
C.2
D.9
3.二次函数y=ax2+bx+c的图象如图所示,则一次函数y=ax+b与反比例函数y=在同一平面直角坐标系内的图象大致为( )
4.如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,给出下列4个结论:①c>0;②若点B,C为函数图象上的两点,则y1A.1个
B.2个
C.3个
D.4个
5.若二次函数y=|a|x2+bx+c的图象经过A(m,n),B(0,y1),C(3-m,n),D(,
y2),E(2,y3),则y1,y2,y3的大小关系是(
)
A.y1<
y2<
y3
B.
y1
<
y3<
y2
C.y3<
y2<
y1
D.
y2<
y3<
y1
6.(2019·陕西)在同一平面直角坐标系中,若抛物线y=x2+(2m-1)x+2m-4与y=x2-(3m+n)x+n关于y轴对称,则符合条件的m,n的值为(
)
A.m=,n=-
B.m=5,n=-6
C.m=-1,n=6
D.m=1,n=-2
7.如图,一边靠墙(墙有足够长),其他三边用20米长的篱笆围成一个矩形(ABCD)花园,这个花园的最大面积是 平方米.(
)
A.40
B.50
C.60
D.以上都不对
8.已知学校航模组设计制作的火箭的升空高度h(m)与飞行时间t(s)满足函数表达式h=-t2+24t+1.则下列说法中正确的是(
)
A.点火后9
s和点火后13
s的升空高度相同
B.点火后24
s火箭落于地面
C.点火后10
s的升空高度为139
m
D.火箭升空的最大高度为145
m
9.(2019年山西省中考)(3分)北中环桥是省城太原的一座跨汾河大桥(如图1),它由五个高度不同,跨径也不同的抛物线型钢拱通过吊桥,拉索与主梁相连,最高的钢拱如图2所示,此钢拱(近似看成二次函数的图象﹣抛物线)在同一竖直平面内,与拱脚所在的水平面相交于A,B两点.拱高为78米(即最高点O到AB的距离为78米),跨径为90米(即AB=90米),以最高点O为坐标原点,以平行于AB的直线为x轴建立平面直角坐标系,则此抛物线钢拱的函数表达式为( )
A.y=x2
B.y=﹣x2
C.y=x2
D.y=﹣x2
10.(2019·淄博)将二次函数y=x2-4x+a的图象向左平移一个单位,再向上平移一个单位,若得到的函数图象与直线y=2有两个交点,则a的取值范围是 ( )
A.a>3
B.a<3
C.a>5
D.a<5
2、填空题
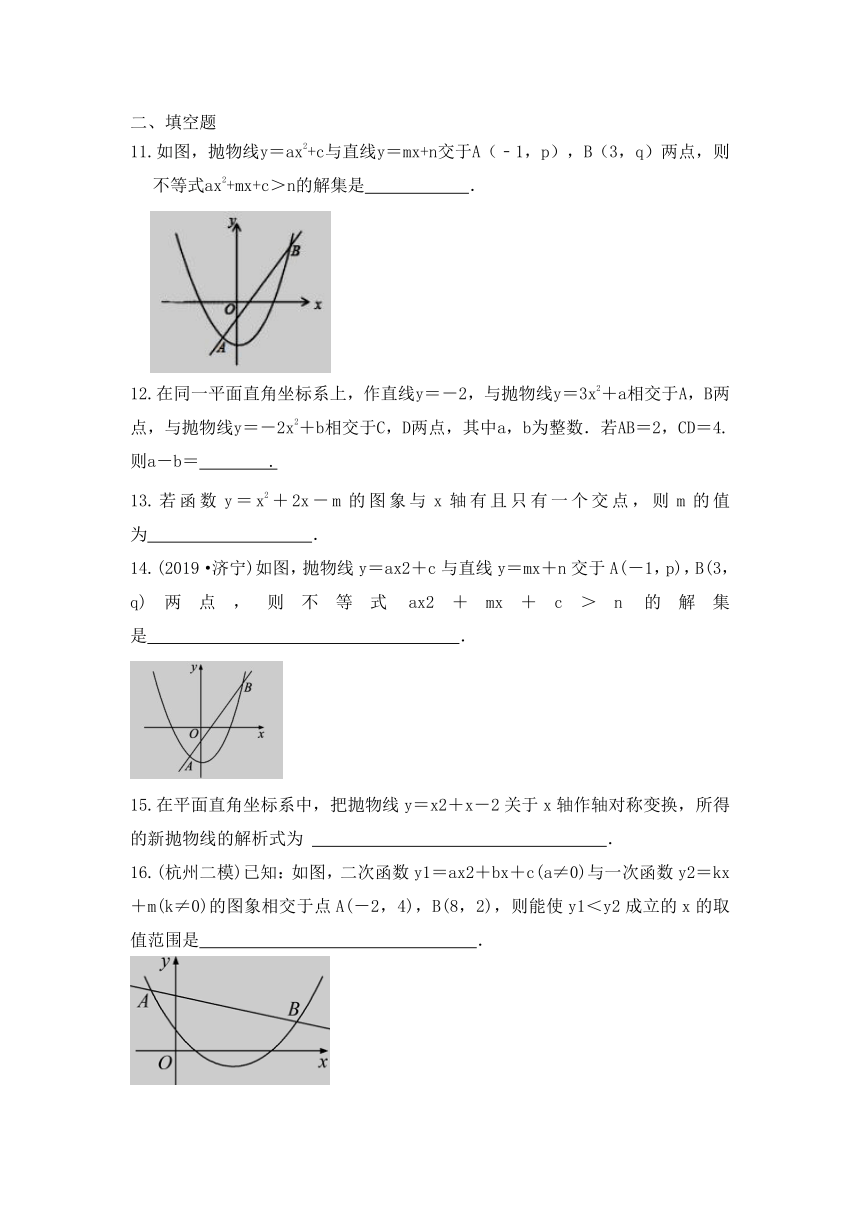
11.如图,抛物线y=ax2+c与直线y=mx+n交于A(﹣1,p),B(3,q)两点,则不等式ax2+mx+c>n的解集是
.
12.在同一平面直角坐标系上,作直线y=-2,与抛物线y=3x2+a相交于A,B两点,与抛物线y=-2x2+b相交于C,D两点,其中a,b为整数.若AB=2,CD=4.则a-b=
.
13.若函数y=x2+2x-m的图象与x轴有且只有一个交点,则m的值为
.
14.(2019·济宁)如图,抛物线y=ax2+c与直线y=mx+n交于A(-1,p),B(3,q)两点,则不等式ax2+mx+c>n的解集是
.
15.在平面直角坐标系中,把抛物线y=x2+x-2关于x轴作轴对称变换,所得的新抛物线的解析式为
.
16.(杭州二模)已知:如图,二次函数y1=ax2+bx+c(a≠0)与一次函数y2=kx+m(k≠0)的图象相交于点A(-2,4),B(8,2),则能使y1<y2成立的x的取值范围是
.
3、综合题
17.二次函数y=ax2+bx+c的图象如图所示,且P=|2a+b|+|3b-2c|,Q=|2a-b|-|3b+2c|,试判断P,Q的大小关系.
18.如图,在平面直角坐标系中,点A(1,2),B(5,0),抛物线y=ax2-2ax(a>0)交x轴正半轴于点C,连结AO,AB.
(1)求点C的坐标和直线AB的表达式;
(2)设抛物线y=ax2-2ax(a>0)分别交边BA,BA延长线于点D,E.
①若AE=3AO,求抛物线表达式;
②若△CDB与△BOA相似,则a的值为 .(请直接写出答案)
19.某乡镇实施产业扶贫,帮助贫困户承包了荒山种植某品种蜜柚.到了收获季节,已知该蜜柚的成本价为8元/kg,投入市场销售时,调查市场行情,发现该蜜柚销售不会亏本,且每天销售量y(kg)与销售单价x(元/kg)之间的函数关系如图所示.
(1)求y与x的函数关系式,并写出x的取值范围;
(2)当该品种蜜柚定价为多少时,每天销售获得的利润最大?最大利润是多少?
(3)某农户今年共采摘蜜柚4
800
kg,该品种蜜柚的保质期为40天,根据(2)中获得最大利润的方式进行销售,能否销售完这批蜜柚?请说明理由.
20.(2019年山西省中考)(13分)综合与探究
如图,抛物线y=ax2+bx+6经过点A(﹣2,0),B(4,0)两点,与y轴交于点C,点D是抛物线上一个动点,设点D的横坐标为m(1<m<4).连接AC,BC,DB,DC.
(1)求抛物线的函数表达式;
(2)△BCD的面积等于△AOC的面积的时,求m的值;
(3)在(2)的条件下,若点M是x轴上一动点,点N是抛物线上一动点,试判断是否存在这样的点M,使得以点B,D,M,N为顶点的四边形是平行四边形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
第1章
二次函数
单元测试(3)答案
1、选择题
1.
C
2.A
3.B
4.
D
5.D
6.D
7.B
8.
D
9.B
10.
D
二、填空题
11.x<﹣3或x>1
12.-11
13.-1
14.x<-3或x>1
15.y=-x2-x+2
16.-2<x<8
三、综合题
17.解:∵抛物线的开口向下,
∴a<0.∵->0,
∴b>0,
∴2a-b<0.
∵-=1,
∴b+2a=0.当x=-1时,y=a-b+c<0,
∴-b-b+c<0,
∴3b-2c>0.
∵抛物线与y轴的正半轴相交,
∴c>0,
∴3b+2c>0,
∴P=3b-2c,Q=b-2a-3b-2c=-2a-2b-2c,
∴Q-P=-2a-2b-2c-3b+2c=-2a-5b=-4b<0.
∴P>Q.
18.解:(1)∵x=-=1,∵O,C两点关于直线x=1对称,∴C(2,0),设直线AB:y=kx+b,把A(1,2),B(5,0)代入得y=-x+;
(2)①∵A(1,2),B(5,0),O(0,0),∴OA=,OB=5,AB=2,∴OA2+AB2=OB2,∴∠OAB=90°,∴∠OAE=90°,作EF⊥AF,AG⊥x轴,∵∠FEA=∠OAG,∠F=∠AGO=90°,∴△EAF∽△AOG,∴==3,∴E(-5,5),代入解析式可得,a=,∴y=x2-x;
②若△CDB与△BOA相似,==,∴==,∴D(,),代入解析式可得a=.
19.解:(1)设y与x的函数关系式为y=kx+b(k≠0).把(10,200),(15,150)代入y=kx+b,得
解得
∴y与x的函数关系式为y=-10x+300.
由-10x+300≥0,得x≤30.
∴x的取值范围为8≤x≤30;
(2)设该品种蜜柚定价为x元/kg时,每天销售利润为W元.根据题意,得
W=(x-8)(-10x+300)
=-10(x-19)2+1
210.
∵a=-10<0,
∴当x=19时,W最大值=1
210.
答:当该品种蜜柚定价为19元/kg时,每天销售获得的利润最大,最大利润是1
210元;
(3)不能.
理由:根据(2)中获得最大利润的方式进行销售时,定价为19元/kg,则
y=-10×19+300=110.
∴110×40=4
400<4
800.
∴该农户不能销售完这批蜜柚.
20.解:(1)由抛物线交点式表达式得:y=a(x+2)(x﹣4)=a(x2﹣2x﹣8)=ax2﹣2ax﹣8a,
即﹣8a=6,解得:a=﹣,
故抛物线的表达式为:y=﹣x2+x+6;
(2)点C(0,6),将点B、C的坐标代入一次函数表达式并解得:
直线BC的表达式为:y=﹣x+6,
如图所示,过点D作y轴的平行线交直线BC与点H,
设点D(m,﹣m2+m+6),则点H(m,﹣m+6)
S△BDC=HB×OB=2(﹣m2+m+6+m﹣6)=﹣m2+3m,
S△ACO=××6×2=,
即:﹣m2+3m=,
解得:m=1或3(舍去1),
故m=3;
(3)当m=3时,点D(3,),
①当BD是平行四边形的一条边时,
M、N分别有三个点,
设点N(n,﹣n2+n+6)
则点N的纵坐标为绝对值为,
即|﹣n2+n+6|=,
解得:n=﹣1或3(舍去)或1,
故点N(N′、N″)的坐标为(﹣1,)或(1+,﹣)或(1﹣,﹣),
当点N(﹣1,)时,由图象可得:点M(0,0),
当N′的坐标为(1+,﹣),由中点坐标公式得:点M′(,0),
同理可得:点M″坐标为(﹣,0),
故点M坐标为:(0,0)或(,0)或(﹣,0);
②当BD是平行四边形的对角线时,
点B、D的坐标分别为(4,0)、(3,)
设点M(m,0),点N(s,t),
由中点坐标公式得:,而t=,
解得:t=,s=﹣1,m=8,
故点M坐标为(8,0);
故点M的坐标为:(0,0)或(,0)或(﹣,0)或(8,0).
二次函数
单元测试(3)
1、选择题
1.已知二次函数y=2x2-3,当-1≤x≤2时,y的取值范围是( )
A.-1≤y≤5
B.-5≤y≤5
C.-3≤y≤5
D.-2≤y≤1
2.当二次函数y=x2+4x+9取最小值时,x的值为( )
A.-2
B.1
C.2
D.9
3.二次函数y=ax2+bx+c的图象如图所示,则一次函数y=ax+b与反比例函数y=在同一平面直角坐标系内的图象大致为( )
4.如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,给出下列4个结论:①c>0;②若点B,C为函数图象上的两点,则y1
B.2个
C.3个
D.4个
5.若二次函数y=|a|x2+bx+c的图象经过A(m,n),B(0,y1),C(3-m,n),D(,
y2),E(2,y3),则y1,y2,y3的大小关系是(
)
A.y1<
y2<
y3
B.
y1
<
y3<
y2
C.y3<
y2<
y1
D.
y2<
y3<
y1
6.(2019·陕西)在同一平面直角坐标系中,若抛物线y=x2+(2m-1)x+2m-4与y=x2-(3m+n)x+n关于y轴对称,则符合条件的m,n的值为(
)
A.m=,n=-
B.m=5,n=-6
C.m=-1,n=6
D.m=1,n=-2
7.如图,一边靠墙(墙有足够长),其他三边用20米长的篱笆围成一个矩形(ABCD)花园,这个花园的最大面积是 平方米.(
)
A.40
B.50
C.60
D.以上都不对
8.已知学校航模组设计制作的火箭的升空高度h(m)与飞行时间t(s)满足函数表达式h=-t2+24t+1.则下列说法中正确的是(
)
A.点火后9
s和点火后13
s的升空高度相同
B.点火后24
s火箭落于地面
C.点火后10
s的升空高度为139
m
D.火箭升空的最大高度为145
m
9.(2019年山西省中考)(3分)北中环桥是省城太原的一座跨汾河大桥(如图1),它由五个高度不同,跨径也不同的抛物线型钢拱通过吊桥,拉索与主梁相连,最高的钢拱如图2所示,此钢拱(近似看成二次函数的图象﹣抛物线)在同一竖直平面内,与拱脚所在的水平面相交于A,B两点.拱高为78米(即最高点O到AB的距离为78米),跨径为90米(即AB=90米),以最高点O为坐标原点,以平行于AB的直线为x轴建立平面直角坐标系,则此抛物线钢拱的函数表达式为( )
A.y=x2
B.y=﹣x2
C.y=x2
D.y=﹣x2
10.(2019·淄博)将二次函数y=x2-4x+a的图象向左平移一个单位,再向上平移一个单位,若得到的函数图象与直线y=2有两个交点,则a的取值范围是 ( )
A.a>3
B.a<3
C.a>5
D.a<5
2、填空题
11.如图,抛物线y=ax2+c与直线y=mx+n交于A(﹣1,p),B(3,q)两点,则不等式ax2+mx+c>n的解集是
.
12.在同一平面直角坐标系上,作直线y=-2,与抛物线y=3x2+a相交于A,B两点,与抛物线y=-2x2+b相交于C,D两点,其中a,b为整数.若AB=2,CD=4.则a-b=
.
13.若函数y=x2+2x-m的图象与x轴有且只有一个交点,则m的值为
.
14.(2019·济宁)如图,抛物线y=ax2+c与直线y=mx+n交于A(-1,p),B(3,q)两点,则不等式ax2+mx+c>n的解集是
.
15.在平面直角坐标系中,把抛物线y=x2+x-2关于x轴作轴对称变换,所得的新抛物线的解析式为
.
16.(杭州二模)已知:如图,二次函数y1=ax2+bx+c(a≠0)与一次函数y2=kx+m(k≠0)的图象相交于点A(-2,4),B(8,2),则能使y1<y2成立的x的取值范围是
.
3、综合题
17.二次函数y=ax2+bx+c的图象如图所示,且P=|2a+b|+|3b-2c|,Q=|2a-b|-|3b+2c|,试判断P,Q的大小关系.
18.如图,在平面直角坐标系中,点A(1,2),B(5,0),抛物线y=ax2-2ax(a>0)交x轴正半轴于点C,连结AO,AB.
(1)求点C的坐标和直线AB的表达式;
(2)设抛物线y=ax2-2ax(a>0)分别交边BA,BA延长线于点D,E.
①若AE=3AO,求抛物线表达式;
②若△CDB与△BOA相似,则a的值为 .(请直接写出答案)
19.某乡镇实施产业扶贫,帮助贫困户承包了荒山种植某品种蜜柚.到了收获季节,已知该蜜柚的成本价为8元/kg,投入市场销售时,调查市场行情,发现该蜜柚销售不会亏本,且每天销售量y(kg)与销售单价x(元/kg)之间的函数关系如图所示.
(1)求y与x的函数关系式,并写出x的取值范围;
(2)当该品种蜜柚定价为多少时,每天销售获得的利润最大?最大利润是多少?
(3)某农户今年共采摘蜜柚4
800
kg,该品种蜜柚的保质期为40天,根据(2)中获得最大利润的方式进行销售,能否销售完这批蜜柚?请说明理由.
20.(2019年山西省中考)(13分)综合与探究
如图,抛物线y=ax2+bx+6经过点A(﹣2,0),B(4,0)两点,与y轴交于点C,点D是抛物线上一个动点,设点D的横坐标为m(1<m<4).连接AC,BC,DB,DC.
(1)求抛物线的函数表达式;
(2)△BCD的面积等于△AOC的面积的时,求m的值;
(3)在(2)的条件下,若点M是x轴上一动点,点N是抛物线上一动点,试判断是否存在这样的点M,使得以点B,D,M,N为顶点的四边形是平行四边形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
第1章
二次函数
单元测试(3)答案
1、选择题
1.
C
2.A
3.B
4.
D
5.D
6.D
7.B
8.
D
9.B
10.
D
二、填空题
11.x<﹣3或x>1
12.-11
13.-1
14.x<-3或x>1
15.y=-x2-x+2
16.-2<x<8
三、综合题
17.解:∵抛物线的开口向下,
∴a<0.∵->0,
∴b>0,
∴2a-b<0.
∵-=1,
∴b+2a=0.当x=-1时,y=a-b+c<0,
∴-b-b+c<0,
∴3b-2c>0.
∵抛物线与y轴的正半轴相交,
∴c>0,
∴3b+2c>0,
∴P=3b-2c,Q=b-2a-3b-2c=-2a-2b-2c,
∴Q-P=-2a-2b-2c-3b+2c=-2a-5b=-4b<0.
∴P>Q.
18.解:(1)∵x=-=1,∵O,C两点关于直线x=1对称,∴C(2,0),设直线AB:y=kx+b,把A(1,2),B(5,0)代入得y=-x+;
(2)①∵A(1,2),B(5,0),O(0,0),∴OA=,OB=5,AB=2,∴OA2+AB2=OB2,∴∠OAB=90°,∴∠OAE=90°,作EF⊥AF,AG⊥x轴,∵∠FEA=∠OAG,∠F=∠AGO=90°,∴△EAF∽△AOG,∴==3,∴E(-5,5),代入解析式可得,a=,∴y=x2-x;
②若△CDB与△BOA相似,==,∴==,∴D(,),代入解析式可得a=.
19.解:(1)设y与x的函数关系式为y=kx+b(k≠0).把(10,200),(15,150)代入y=kx+b,得
解得
∴y与x的函数关系式为y=-10x+300.
由-10x+300≥0,得x≤30.
∴x的取值范围为8≤x≤30;
(2)设该品种蜜柚定价为x元/kg时,每天销售利润为W元.根据题意,得
W=(x-8)(-10x+300)
=-10(x-19)2+1
210.
∵a=-10<0,
∴当x=19时,W最大值=1
210.
答:当该品种蜜柚定价为19元/kg时,每天销售获得的利润最大,最大利润是1
210元;
(3)不能.
理由:根据(2)中获得最大利润的方式进行销售时,定价为19元/kg,则
y=-10×19+300=110.
∴110×40=4
400<4
800.
∴该农户不能销售完这批蜜柚.
20.解:(1)由抛物线交点式表达式得:y=a(x+2)(x﹣4)=a(x2﹣2x﹣8)=ax2﹣2ax﹣8a,
即﹣8a=6,解得:a=﹣,
故抛物线的表达式为:y=﹣x2+x+6;
(2)点C(0,6),将点B、C的坐标代入一次函数表达式并解得:
直线BC的表达式为:y=﹣x+6,
如图所示,过点D作y轴的平行线交直线BC与点H,
设点D(m,﹣m2+m+6),则点H(m,﹣m+6)
S△BDC=HB×OB=2(﹣m2+m+6+m﹣6)=﹣m2+3m,
S△ACO=××6×2=,
即:﹣m2+3m=,
解得:m=1或3(舍去1),
故m=3;
(3)当m=3时,点D(3,),
①当BD是平行四边形的一条边时,
M、N分别有三个点,
设点N(n,﹣n2+n+6)
则点N的纵坐标为绝对值为,
即|﹣n2+n+6|=,
解得:n=﹣1或3(舍去)或1,
故点N(N′、N″)的坐标为(﹣1,)或(1+,﹣)或(1﹣,﹣),
当点N(﹣1,)时,由图象可得:点M(0,0),
当N′的坐标为(1+,﹣),由中点坐标公式得:点M′(,0),
同理可得:点M″坐标为(﹣,0),
故点M坐标为:(0,0)或(,0)或(﹣,0);
②当BD是平行四边形的对角线时,
点B、D的坐标分别为(4,0)、(3,)
设点M(m,0),点N(s,t),
由中点坐标公式得:,而t=,
解得:t=,s=﹣1,m=8,
故点M坐标为(8,0);
故点M的坐标为:(0,0)或(,0)或(﹣,0)或(8,0).
