19.2.3 平行四边形的判定1课件(共26张PPT)
文档属性
| 名称 | 19.2.3 平行四边形的判定1课件(共26张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-25 21:50:29 | ||
图片预览






文档简介
(共26张PPT)
19.2.3
平行四边形的判定
沪科版
八年级下
新知导入
问题1.平行四边形具有哪些性质?
1.边:对边平行且相等;
2.角:对角相等,邻角互补;
3.对角线:对角线互相平分.
问题2.如何判定一个四边形是平行四边形呢?
我们可以用平行四边形的定义来判定,即两组对边分别平行的四边形是平行四边形.除了这种判定方法外,我们还可以用其他方法来判定一个四边形是平行四边形吗?
新知讲解
探索1:将线段AB按所给的方向和距离,平移成线段A'B',顺次连接A,B,B',A',构成一个一组对边平行且相等的四边形ABB'A',你能说出他一定是平行四边形吗?
已知:在四边形ABB'A'中,AB=A'B',AB‖
A'B'
求证:四边形ABB'A'是平行四边形.
同学们,根据你们现学的知识可以证明这个结论吗?
新知讲解
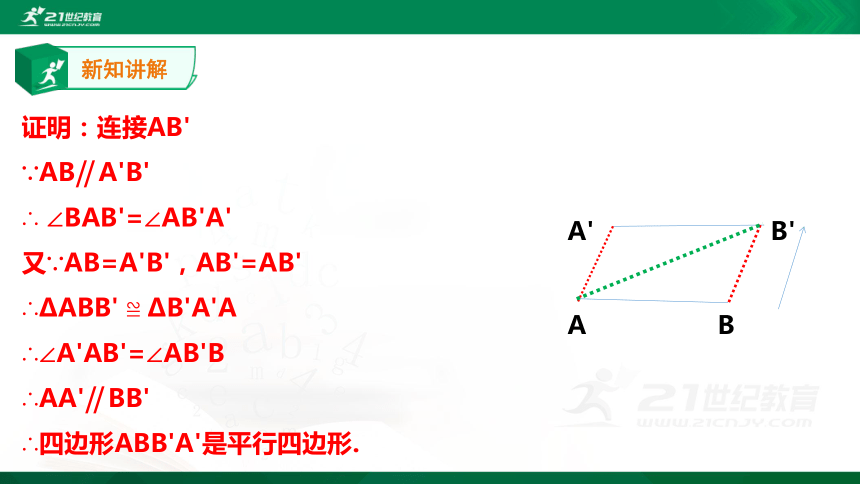
证明:连接AB'
∵AB‖
A'B'
∴
∠BAB'=∠AB'A'
又∵AB=A'B',AB'=AB'
∴?ABB'
≌
?B'A'A
∴∠A'AB'=∠AB'B
∴AA'‖
BB'
∴四边形ABB'A'是平行四边形.
新知讲解
归纳小结:
由此我们可以得到如下判定四边形是否为平行四边形的方法:
定理1:一组对边平行且相等的四边形是平行四边形.
几何语言:
∵AB=A'B',AB‖
A'B'
∴四边形ABB'A'是平行四边形.
同学们,平行四边形还有其他的判定方法吗?
新知讲解
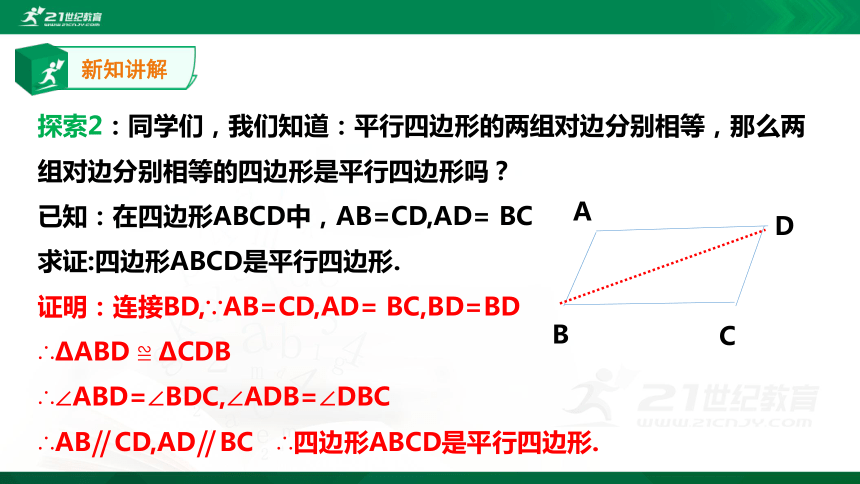
探索2:同学们,我们知道:平行四边形的两组对边分别相等,那么两组对边分别相等的四边形是平行四边形吗?
已知:在四边形ABCD中,AB=CD,AD=
BC
求证:四边形ABCD是平行四边形.
证明:连接BD,∵AB=CD,AD=
BC,BD=BD
∴?ABD
≌
?CDB
∴∠ABD=∠BDC,∠ADB=∠DBC
∴AB‖
CD,AD‖
BC
∴四边形ABCD是平行四边形.
新知讲解
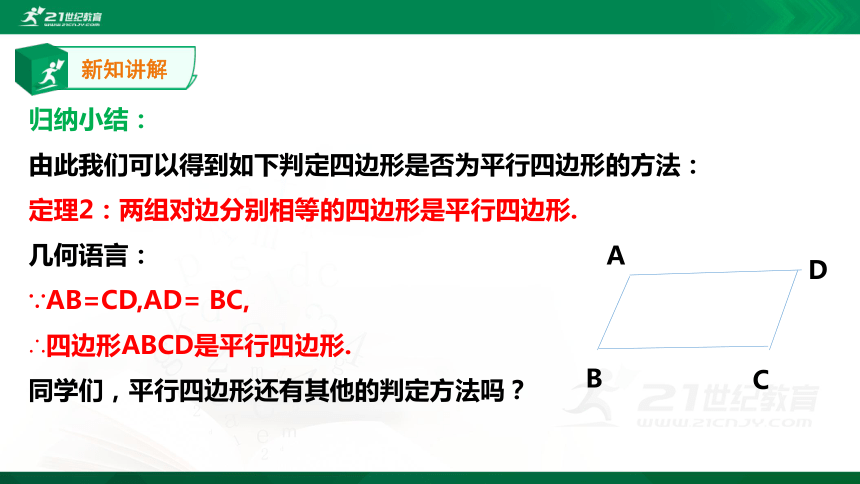
归纳小结:
由此我们可以得到如下判定四边形是否为平行四边形的方法:
定理2:两组对边分别相等的四边形是平行四边形.
几何语言:
∵AB=CD,AD=
BC,
∴四边形ABCD是平行四边形.
同学们,平行四边形还有其他的判定方法吗?
新知讲解
探索3:同学们,我们知道:平行四边形的两条对角线互相平分,那么两条对角线互相平分的四边形是平行四边形吗?
已知:在四边形ABCD中,对角线AC,BD相较于O,并且AO=CO,BO=DO.
求证:四边形ABCD是平行四边形.
证明:∵AO=CO,BO=DO,∠AOB=∠COD
∴?AOB
≌
?COD
∴AB=CD,∠ABO=∠ODC
∴AB‖
CD,
∴四边形ABCD是平行四边形.
新知讲解
归纳小结:
由此我们可以得到如下判定四边形是否为平行四边形的方法:
定理3:两条对角线互相平分的四边形是平行四边形
几何语言:
∵AO=CO,OD=
BO,
∴四边形ABCD是平行四边形.
新知讲解
例1.
如图
,在平行四边形ABCD
中,E,F
分别是AB,CD
的中点.求证:四边形EBFD
是平行四边形.
证明:
∵四边形ABCD
是平行四边形,
∴AB
=CD,EB
//
FD.
又
∵
∴EB
=FD
.
∴四边形EBFD
是平行四边形.
新知讲解
例2.
如图,在Rt△MON中,∠MON=90°.求证:
四边形PONM是平行四边形.
证明:Rt△MON
中,
由勾股定理得(x-5)2+42=(x-3)2,
解得x=8.
∴PM=11-x=3,ON=x-5=3,MN=x-3=5.
∴PM=ON,OP=MN,
∴四边形PONM是平行四边形.
新知讲解
例3.如图,
□ABCD
的对角线AC,BD
相交于点O,E,F
是AC上的两点,并且AE=CF.求证:四边形BFDE
是平行四边形.
证明:∵四边形ABCD
是平行四边形,
∴
AO=CO,BO=DO.
∵AE=CF
,
∴
AO-AE=CO-CF,即EO=OF.
又∵BO=DO,
∴四边形BFDE
是平行四边形.
课堂练习
1.判断对错:
(1)有一组对边平行的四边形是平行四边形.
(
)
(2)有两条边相等并且另外两条边也相等的四边形一定
是平行四边形.
(
)
(3)对角线互相平分的四边形是平行四边形.
(
)
(4)一条对角线平分另一条对角线的四边形是平行四边形.
(
)
(5)有一组对角相等且一组对边平行的四边形是平行
四边形.
(
)
×
×
√
×
√
课堂练习
2.已知四边形ABCD
中有四个条件:AB∥CD,AB=CD,BC∥AD,BC
=AD,从中任选两个,不能使四边形ABCD
成为平行四边形的选法
是
( )
A.AB∥CD,AB=CD
B.AB∥CD,BC∥AD
C.AB∥CD,BC=AD
D.AB=CD,BC=AD
C
课堂练习
3.四边形AEFD
和EBCF
都是平行四边形,求证:四边形ABCD
是平行四边形.
证明:∵四边形AEFD
和EBCF
都是平行四边形,
∴AD∥
EF,AD=EF,
EF∥
BC,
EF=BC.
∴AD∥
BC,AD=BC.
∴四边形ABCD
是平行四边形.
课堂练习
4.如图,
AD⊥AC,BC⊥AC,且AB=CD,
求证:四边形ABCD是平行四边形.
证明:在Rt△ABC
和Rt△CDA
中,
∵AC=CA,AB=CD,
∴Rt△ABC
≌
Rt△CDA(HL),
∴BC=DA.
又∵AB=CD,
∴四边形ABCD
是平行四边形.
课堂练习
5.如图,AB、CD
相交于点O,AC∥DB,AO=BO,E、F
分别是OC、OD
中点.求证:(1)△AOC
≌
△BOD;(2)四边形AFBE
是平行四边形.
证明:(1)∵AC∥BD,
∴∠C=∠D.
又∵∠COA=∠DOB,AO=BO
,
∴△AOC
≌△BOD
(AAS);
(2)∵△AOC
≌
△BOD,
∴CO=DO.
∵E、F
分别是OC、OD
的中点,
∴EO=FO.
又∵AO=BO,
∴四边形AFBE
是平行四边形.
拓展提高
6.如图,在四边形ABCD
中,AD∥BC,AD=12cm,BC=15cm,点P
自点A
向D
以1cm/s的速度运动,到D
点即停止.点Q
自点C
向B
以2cm/s的速度运动,到B
点即停止,点P,Q
同时出发,设运动时间为t(s).
(1)用含t
的代数式表示:
AP=_____;
DP=________;
BQ=________;
CQ=________;
tcm
(12-t)cm
(15-2t)cm
2tcm
拓展提高
(2)当t
为何值时,四边形APQB
是平行四边形?
解:根据题意有AP=tcm,BQ=(15-2t
)cm.
∵AD∥BC,
∴当AP
=BQ
时,四边形APQB
是平行四边形.
∴t=15-2t,
解得t=5.
∴t=5s时四边形APQB
是平行四边形;
拓展提高
(3)当t
为何值时,四边形PDCQ
是平行四边形?
解:∵AP=t
cm,∴PD=AD-AP=12-t,
CQ=2t
cm,
又∵AD∥BC,
∴当PD=QC
时,四边形PDCQ
是平行四边形.
即12-t=2t,
解得t=4s,
∴当t=4s时,四边形PDCQ
是平行四边形.
中考链接
7.(太仓
中考)已知四边形ABCD
中,AB∥CD,AB=CD,周长为40cm,两邻边的比是3:2,则较大边的长度是(
)
A.8cm
B.10cm
C.12cm
D.14cm
8.(泰州
中考)如图,在平行四边形ABCD
中,EF∥AD,HN∥AB,则图中的平行四边形的个数共有____个.
C
9
课堂总结
本节课你有什么收获?
定理1:一组对边平行且相等的四边形是平行四边形.
定理2:两组对边分别相等的四边形是平行四边形.
定理3:两条对角线互相平分的四边形是平行四边形
板书设计
19.2.3平行四边形的判定
定理1:
定理2:
定理3:
作业布置
课本
P85
习题
第9/10/11/12题.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
19.2.3
平行四边形的判定
沪科版
八年级下
新知导入
问题1.平行四边形具有哪些性质?
1.边:对边平行且相等;
2.角:对角相等,邻角互补;
3.对角线:对角线互相平分.
问题2.如何判定一个四边形是平行四边形呢?
我们可以用平行四边形的定义来判定,即两组对边分别平行的四边形是平行四边形.除了这种判定方法外,我们还可以用其他方法来判定一个四边形是平行四边形吗?
新知讲解
探索1:将线段AB按所给的方向和距离,平移成线段A'B',顺次连接A,B,B',A',构成一个一组对边平行且相等的四边形ABB'A',你能说出他一定是平行四边形吗?
已知:在四边形ABB'A'中,AB=A'B',AB‖
A'B'
求证:四边形ABB'A'是平行四边形.
同学们,根据你们现学的知识可以证明这个结论吗?
新知讲解
证明:连接AB'
∵AB‖
A'B'
∴
∠BAB'=∠AB'A'
又∵AB=A'B',AB'=AB'
∴?ABB'
≌
?B'A'A
∴∠A'AB'=∠AB'B
∴AA'‖
BB'
∴四边形ABB'A'是平行四边形.
新知讲解
归纳小结:
由此我们可以得到如下判定四边形是否为平行四边形的方法:
定理1:一组对边平行且相等的四边形是平行四边形.
几何语言:
∵AB=A'B',AB‖
A'B'
∴四边形ABB'A'是平行四边形.
同学们,平行四边形还有其他的判定方法吗?
新知讲解
探索2:同学们,我们知道:平行四边形的两组对边分别相等,那么两组对边分别相等的四边形是平行四边形吗?
已知:在四边形ABCD中,AB=CD,AD=
BC
求证:四边形ABCD是平行四边形.
证明:连接BD,∵AB=CD,AD=
BC,BD=BD
∴?ABD
≌
?CDB
∴∠ABD=∠BDC,∠ADB=∠DBC
∴AB‖
CD,AD‖
BC
∴四边形ABCD是平行四边形.
新知讲解
归纳小结:
由此我们可以得到如下判定四边形是否为平行四边形的方法:
定理2:两组对边分别相等的四边形是平行四边形.
几何语言:
∵AB=CD,AD=
BC,
∴四边形ABCD是平行四边形.
同学们,平行四边形还有其他的判定方法吗?
新知讲解
探索3:同学们,我们知道:平行四边形的两条对角线互相平分,那么两条对角线互相平分的四边形是平行四边形吗?
已知:在四边形ABCD中,对角线AC,BD相较于O,并且AO=CO,BO=DO.
求证:四边形ABCD是平行四边形.
证明:∵AO=CO,BO=DO,∠AOB=∠COD
∴?AOB
≌
?COD
∴AB=CD,∠ABO=∠ODC
∴AB‖
CD,
∴四边形ABCD是平行四边形.
新知讲解
归纳小结:
由此我们可以得到如下判定四边形是否为平行四边形的方法:
定理3:两条对角线互相平分的四边形是平行四边形
几何语言:
∵AO=CO,OD=
BO,
∴四边形ABCD是平行四边形.
新知讲解
例1.
如图
,在平行四边形ABCD
中,E,F
分别是AB,CD
的中点.求证:四边形EBFD
是平行四边形.
证明:
∵四边形ABCD
是平行四边形,
∴AB
=CD,EB
//
FD.
又
∵
∴EB
=FD
.
∴四边形EBFD
是平行四边形.
新知讲解
例2.
如图,在Rt△MON中,∠MON=90°.求证:
四边形PONM是平行四边形.
证明:Rt△MON
中,
由勾股定理得(x-5)2+42=(x-3)2,
解得x=8.
∴PM=11-x=3,ON=x-5=3,MN=x-3=5.
∴PM=ON,OP=MN,
∴四边形PONM是平行四边形.
新知讲解
例3.如图,
□ABCD
的对角线AC,BD
相交于点O,E,F
是AC上的两点,并且AE=CF.求证:四边形BFDE
是平行四边形.
证明:∵四边形ABCD
是平行四边形,
∴
AO=CO,BO=DO.
∵AE=CF
,
∴
AO-AE=CO-CF,即EO=OF.
又∵BO=DO,
∴四边形BFDE
是平行四边形.
课堂练习
1.判断对错:
(1)有一组对边平行的四边形是平行四边形.
(
)
(2)有两条边相等并且另外两条边也相等的四边形一定
是平行四边形.
(
)
(3)对角线互相平分的四边形是平行四边形.
(
)
(4)一条对角线平分另一条对角线的四边形是平行四边形.
(
)
(5)有一组对角相等且一组对边平行的四边形是平行
四边形.
(
)
×
×
√
×
√
课堂练习
2.已知四边形ABCD
中有四个条件:AB∥CD,AB=CD,BC∥AD,BC
=AD,从中任选两个,不能使四边形ABCD
成为平行四边形的选法
是
( )
A.AB∥CD,AB=CD
B.AB∥CD,BC∥AD
C.AB∥CD,BC=AD
D.AB=CD,BC=AD
C
课堂练习
3.四边形AEFD
和EBCF
都是平行四边形,求证:四边形ABCD
是平行四边形.
证明:∵四边形AEFD
和EBCF
都是平行四边形,
∴AD∥
EF,AD=EF,
EF∥
BC,
EF=BC.
∴AD∥
BC,AD=BC.
∴四边形ABCD
是平行四边形.
课堂练习
4.如图,
AD⊥AC,BC⊥AC,且AB=CD,
求证:四边形ABCD是平行四边形.
证明:在Rt△ABC
和Rt△CDA
中,
∵AC=CA,AB=CD,
∴Rt△ABC
≌
Rt△CDA(HL),
∴BC=DA.
又∵AB=CD,
∴四边形ABCD
是平行四边形.
课堂练习
5.如图,AB、CD
相交于点O,AC∥DB,AO=BO,E、F
分别是OC、OD
中点.求证:(1)△AOC
≌
△BOD;(2)四边形AFBE
是平行四边形.
证明:(1)∵AC∥BD,
∴∠C=∠D.
又∵∠COA=∠DOB,AO=BO
,
∴△AOC
≌△BOD
(AAS);
(2)∵△AOC
≌
△BOD,
∴CO=DO.
∵E、F
分别是OC、OD
的中点,
∴EO=FO.
又∵AO=BO,
∴四边形AFBE
是平行四边形.
拓展提高
6.如图,在四边形ABCD
中,AD∥BC,AD=12cm,BC=15cm,点P
自点A
向D
以1cm/s的速度运动,到D
点即停止.点Q
自点C
向B
以2cm/s的速度运动,到B
点即停止,点P,Q
同时出发,设运动时间为t(s).
(1)用含t
的代数式表示:
AP=_____;
DP=________;
BQ=________;
CQ=________;
tcm
(12-t)cm
(15-2t)cm
2tcm
拓展提高
(2)当t
为何值时,四边形APQB
是平行四边形?
解:根据题意有AP=tcm,BQ=(15-2t
)cm.
∵AD∥BC,
∴当AP
=BQ
时,四边形APQB
是平行四边形.
∴t=15-2t,
解得t=5.
∴t=5s时四边形APQB
是平行四边形;
拓展提高
(3)当t
为何值时,四边形PDCQ
是平行四边形?
解:∵AP=t
cm,∴PD=AD-AP=12-t,
CQ=2t
cm,
又∵AD∥BC,
∴当PD=QC
时,四边形PDCQ
是平行四边形.
即12-t=2t,
解得t=4s,
∴当t=4s时,四边形PDCQ
是平行四边形.
中考链接
7.(太仓
中考)已知四边形ABCD
中,AB∥CD,AB=CD,周长为40cm,两邻边的比是3:2,则较大边的长度是(
)
A.8cm
B.10cm
C.12cm
D.14cm
8.(泰州
中考)如图,在平行四边形ABCD
中,EF∥AD,HN∥AB,则图中的平行四边形的个数共有____个.
C
9
课堂总结
本节课你有什么收获?
定理1:一组对边平行且相等的四边形是平行四边形.
定理2:两组对边分别相等的四边形是平行四边形.
定理3:两条对角线互相平分的四边形是平行四边形
板书设计
19.2.3平行四边形的判定
定理1:
定理2:
定理3:
作业布置
课本
P85
习题
第9/10/11/12题.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
