高中数学人教A版必修4第一章1.4.1正弦函数、余弦函数的图象教案(不含答案)
文档属性
| 名称 | 高中数学人教A版必修4第一章1.4.1正弦函数、余弦函数的图象教案(不含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 91.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-26 00:00:00 | ||
图片预览

文档简介
课题
1.4.1《正弦函数、余弦函数的图象》
课型
新授课
课时
1
教学目标
利用单位圆中的三角函数线作出的图象,明确图象的形状;
(3)用“五点法”作出正弦函数、余弦函数的简图,并利用图象解决一些有关问题;[来源:
教学重点
“五点法”画长度为一个周期的闭区间上的正弦函数图象;
教学难点
运用几何法画正弦函数图象。
教学过程
说明
导
入
新
知
我们之前说三角函数之所以称之为函数,是因为它满足了函数的所有特性。
在三角函数中
,自变量是角,函数值是坐标的比值。
但是在我们之前学习的函数中,自变量都是用x表示,函数值都是用y表示,
所以为了统一,我们将三角函数的自变量由角替换成x,函数值由坐标的比值替换成y。
所以三角函数变为
,除了像这样用解析式表示函数以外,还可以用图像法和列表法表示。
本节课我们就先来学习正弦函数和余弦函数的图像
探
究
新
知
1、正弦函数图像
回想一下,初中我们画函数图像有哪几个步骤?一、列表。二、描点。三、连线。
首先我们来画正弦函数y=sinx的图象
第一步:列表(找特殊值)
x0
........
y
0
1
0.........
第二步:描点
第三步:连线(我们先将[0,2π]之间的点用光滑的曲线连上)
我发现在[0,2π]之间正弦函数图像是一个波浪形的曲线。
我们再画2π之后的图像。还是取特殊值应该是2π、2π+π/6、2π+π/4..…2π+π、2π+(π+π/6)..…4π
x
.....y0.....
我们发现π/6与2π+π/6角的终边相同。根据终边相同的角的同名三角函数值相同,所以π/6与2π+π/6角的正弦值相同,都为1/2。以此类推我们可以画出[2π,4π]的正弦函数图像。
可以发现。[2π,4π]的图像。重复循环[0,2π]的图像。同理,[4π,6π],[6π,8π],……的图像也是一样,重复循环[0,2π],就是由终边相同的角的同名三角函数值相同得出的。
除此之外,我们还可以用平移进行解释。我们只要画出y=sinx,x∈[0,2π]的图象
然后每次沿x轴向右平移2π个单位长度。就能得到x≥0时的所有的函数图像。
具体根据初中所学函数平移特点。自变量平移:左加右减。
函数值平移:上加下减。
由y=sinx,x∈[0,2π]的图象首先向右平移2π个单位长度,即:y=sin(x-2π)=y=sinx,得到x∈[2π,4π]的图象,这样不断的平移就得到了y=sinx,x≥0时的图像。
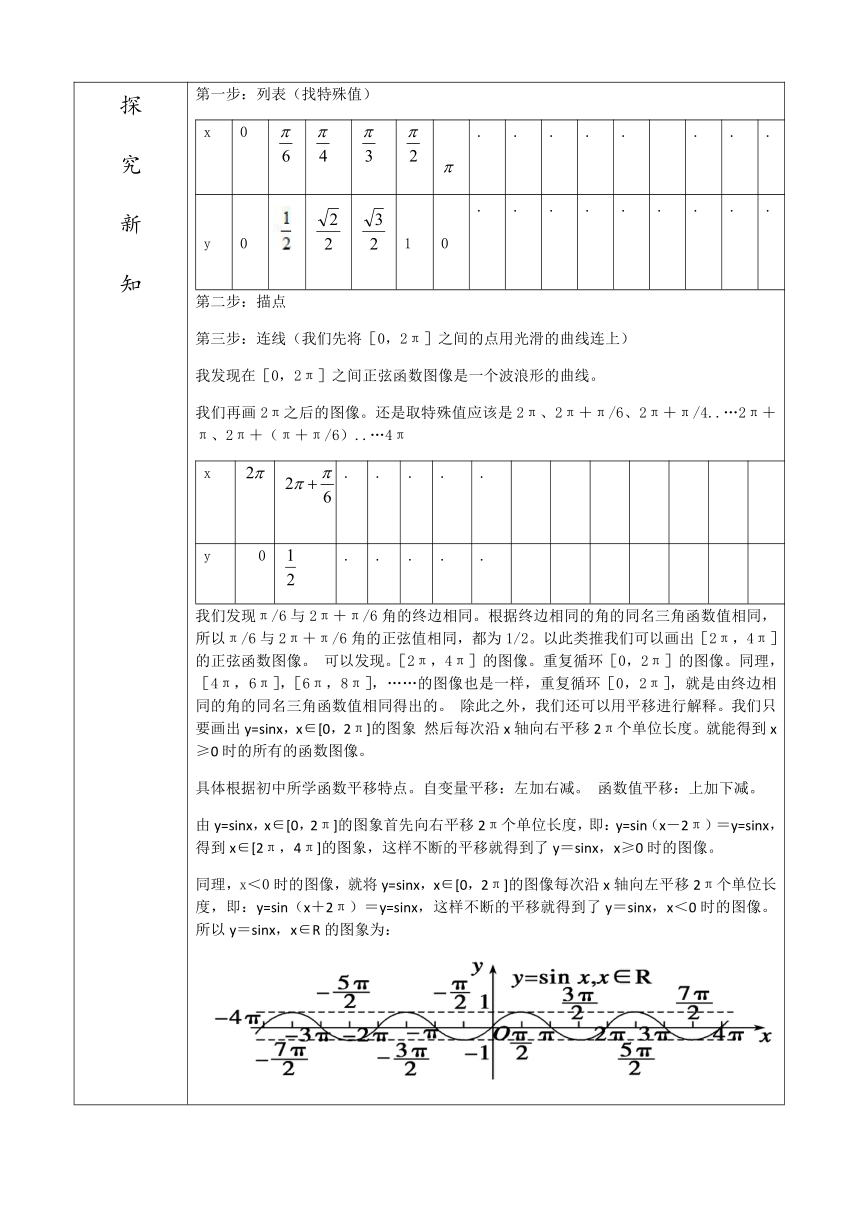
同理,x<0时的图像,就将y=sinx,x∈[0,2π]的图像每次沿x轴向左平移2π个单位长度,即:y=sin(x+2π)=y=sinx,这样不断的平移就得到了y=sinx,x<0时的图像。所以y=sinx,x∈R的图象为:
我们把正弦函数y=sinx,x∈R的图像叫正弦曲线。
思考:做正弦函数图像时,应抓住哪些关键因素?
第一,画[0,2π]的图象即可。
第二,找关键点。
犹如确定直线一样,只需要知道直线上两点即可。但对于正弦曲线而言,我们只需要知道哪几个关键点就可以画出简图了?
(五点,(0,0)、(π/2,1)、(π,0)、(3π/2,2)、(2π,0)。
将着五点用平滑曲线将各个点连接起来,这样就得到了y=sinx,x∈[0,2π]区间的函数图像。然后再通过向左、向右每次平移2π个单位长度。就得到正弦函数y=sinx,x∈R的图像。
因此当精确度要求不太高时,我们常常先找出这五个关键点,再用平滑的曲线将它们连接起来。就得到了在相应区间内正弦函数的简图,这种作图方法叫五点画图法,简称五点法。
2、余弦函数图像
下面我们看余弦函数图像怎么画?
我们也可以用特殊点进行列表、描点、连线。但是由诱导公式sin(x+π/2)=cosx可知。正弦函数y=sin(x+π/2)的图象就是y=cosx的图像。而y=sin(x+π/2)的图象由y=sinx图像向左平移π/2单位长度得到的。
即:y=sinx左移π/2个单位
y=sin(x+π/2)→y=cosx
这种方法简便易行。
除此之外,我们知道正弦函数图像可由y=sinx,x∈[0,2π]的图象连续左右平移2π个单位长度获得。那么,余弦函数是否也可以通过[0,2π]区间的图像平移获得?我们发现也是可以的。所以画余弦函数图像也只画出y=cosx[0,2π]区间的图像,然后左右每次平移2π个单位长度,就得到y=cosx
,x∈R的图像了。
余弦函数图像为:
我们把余弦函数y=cosx
,x∈R的图像叫余弦曲线。
思考:做余弦函数图像时,应抓住哪些关键因素?
第一,画[0,2π]的图象即可。
第二,找关键点。
正弦曲线是五点,那么余弦曲线呢?
(五点,(0,1)、(π/2,0)、(π,-1)、(3π/2,0)、(2π,1)。也是五点画图法)。
巩
固
练
习
1、如何快速地画出正弦函数的图象?
2、如何快速地画出余弦函数的图像?
画出下列函数的简图:
(1)y=2+sinx
,x∈〔0,2π〕
(2)y=-cosx
-1
,x∈〔0,2π〕
[来源:学科网ZXXK]
4、画出下列函数的简图:(1)
y=|sinx|,
(2)y=sin|x|
5、
用五点法作的图象.
6、 结合图象,判断方程的实数解的个数.
课
堂
总
结
.
知
识
点
1.分别画正弦函数y=sinx,x∈R和余弦函数y=cosx
,x∈R的图像。
2.“五点法”画图
画正弦函数y=sin?x,x∈[0,2π]的图象,五个关键点是_________________________;
画余弦函数y=cos?x,x∈[0,2π]的图象,五个关键点是__________________________.
3.正、余弦曲线的联系
依据诱导公式cosx=sin(x+π/2),要得到y=cosx的图象,只需把y=sinx的图象向________平移个
单位长度即可.
布
置
作
业
课本34页,第1、2题
课本习题1.4A组第一题
板
书
设
计
正弦函数图像
余弦函数图像
五点画图法:0、π/2、π、3π/2、2π。
1.4.1《正弦函数、余弦函数的图象》
课型
新授课
课时
1
教学目标
利用单位圆中的三角函数线作出的图象,明确图象的形状;
(3)用“五点法”作出正弦函数、余弦函数的简图,并利用图象解决一些有关问题;[来源:
教学重点
“五点法”画长度为一个周期的闭区间上的正弦函数图象;
教学难点
运用几何法画正弦函数图象。
教学过程
说明
导
入
新
知
我们之前说三角函数之所以称之为函数,是因为它满足了函数的所有特性。
在三角函数中
,自变量是角,函数值是坐标的比值。
但是在我们之前学习的函数中,自变量都是用x表示,函数值都是用y表示,
所以为了统一,我们将三角函数的自变量由角替换成x,函数值由坐标的比值替换成y。
所以三角函数变为
,除了像这样用解析式表示函数以外,还可以用图像法和列表法表示。
本节课我们就先来学习正弦函数和余弦函数的图像
探
究
新
知
1、正弦函数图像
回想一下,初中我们画函数图像有哪几个步骤?一、列表。二、描点。三、连线。
首先我们来画正弦函数y=sinx的图象
第一步:列表(找特殊值)
x0
........
y
0
1
0.........
第二步:描点
第三步:连线(我们先将[0,2π]之间的点用光滑的曲线连上)
我发现在[0,2π]之间正弦函数图像是一个波浪形的曲线。
我们再画2π之后的图像。还是取特殊值应该是2π、2π+π/6、2π+π/4..…2π+π、2π+(π+π/6)..…4π
x
.....y0.....
我们发现π/6与2π+π/6角的终边相同。根据终边相同的角的同名三角函数值相同,所以π/6与2π+π/6角的正弦值相同,都为1/2。以此类推我们可以画出[2π,4π]的正弦函数图像。
可以发现。[2π,4π]的图像。重复循环[0,2π]的图像。同理,[4π,6π],[6π,8π],……的图像也是一样,重复循环[0,2π],就是由终边相同的角的同名三角函数值相同得出的。
除此之外,我们还可以用平移进行解释。我们只要画出y=sinx,x∈[0,2π]的图象
然后每次沿x轴向右平移2π个单位长度。就能得到x≥0时的所有的函数图像。
具体根据初中所学函数平移特点。自变量平移:左加右减。
函数值平移:上加下减。
由y=sinx,x∈[0,2π]的图象首先向右平移2π个单位长度,即:y=sin(x-2π)=y=sinx,得到x∈[2π,4π]的图象,这样不断的平移就得到了y=sinx,x≥0时的图像。
同理,x<0时的图像,就将y=sinx,x∈[0,2π]的图像每次沿x轴向左平移2π个单位长度,即:y=sin(x+2π)=y=sinx,这样不断的平移就得到了y=sinx,x<0时的图像。所以y=sinx,x∈R的图象为:
我们把正弦函数y=sinx,x∈R的图像叫正弦曲线。
思考:做正弦函数图像时,应抓住哪些关键因素?
第一,画[0,2π]的图象即可。
第二,找关键点。
犹如确定直线一样,只需要知道直线上两点即可。但对于正弦曲线而言,我们只需要知道哪几个关键点就可以画出简图了?
(五点,(0,0)、(π/2,1)、(π,0)、(3π/2,2)、(2π,0)。
将着五点用平滑曲线将各个点连接起来,这样就得到了y=sinx,x∈[0,2π]区间的函数图像。然后再通过向左、向右每次平移2π个单位长度。就得到正弦函数y=sinx,x∈R的图像。
因此当精确度要求不太高时,我们常常先找出这五个关键点,再用平滑的曲线将它们连接起来。就得到了在相应区间内正弦函数的简图,这种作图方法叫五点画图法,简称五点法。
2、余弦函数图像
下面我们看余弦函数图像怎么画?
我们也可以用特殊点进行列表、描点、连线。但是由诱导公式sin(x+π/2)=cosx可知。正弦函数y=sin(x+π/2)的图象就是y=cosx的图像。而y=sin(x+π/2)的图象由y=sinx图像向左平移π/2单位长度得到的。
即:y=sinx左移π/2个单位
y=sin(x+π/2)→y=cosx
这种方法简便易行。
除此之外,我们知道正弦函数图像可由y=sinx,x∈[0,2π]的图象连续左右平移2π个单位长度获得。那么,余弦函数是否也可以通过[0,2π]区间的图像平移获得?我们发现也是可以的。所以画余弦函数图像也只画出y=cosx[0,2π]区间的图像,然后左右每次平移2π个单位长度,就得到y=cosx
,x∈R的图像了。
余弦函数图像为:
我们把余弦函数y=cosx
,x∈R的图像叫余弦曲线。
思考:做余弦函数图像时,应抓住哪些关键因素?
第一,画[0,2π]的图象即可。
第二,找关键点。
正弦曲线是五点,那么余弦曲线呢?
(五点,(0,1)、(π/2,0)、(π,-1)、(3π/2,0)、(2π,1)。也是五点画图法)。
巩
固
练
习
1、如何快速地画出正弦函数的图象?
2、如何快速地画出余弦函数的图像?
画出下列函数的简图:
(1)y=2+sinx
,x∈〔0,2π〕
(2)y=-cosx
-1
,x∈〔0,2π〕
[来源:学科网ZXXK]
4、画出下列函数的简图:(1)
y=|sinx|,
(2)y=sin|x|
5、
用五点法作的图象.
6、 结合图象,判断方程的实数解的个数.
课
堂
总
结
.
知
识
点
1.分别画正弦函数y=sinx,x∈R和余弦函数y=cosx
,x∈R的图像。
2.“五点法”画图
画正弦函数y=sin?x,x∈[0,2π]的图象,五个关键点是_________________________;
画余弦函数y=cos?x,x∈[0,2π]的图象,五个关键点是__________________________.
3.正、余弦曲线的联系
依据诱导公式cosx=sin(x+π/2),要得到y=cosx的图象,只需把y=sinx的图象向________平移个
单位长度即可.
布
置
作
业
课本34页,第1、2题
课本习题1.4A组第一题
板
书
设
计
正弦函数图像
余弦函数图像
五点画图法:0、π/2、π、3π/2、2π。
