沪教版数学高一下册-5.4 基于HPM视角下的两角和正余弦展开公式由来的研究 课件(共29张PPT)
文档属性
| 名称 | 沪教版数学高一下册-5.4 基于HPM视角下的两角和正余弦展开公式由来的研究 课件(共29张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 691.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-27 00:15:24 | ||
图片预览



文档简介
(共29张PPT)
基于HPM视角下的两角和正余弦展开公式由来的研究
问题:
思考:
核心问题
已知
的六个三角比的值
求值:
两角和与差的正余弦公式常常被称为平面三角学的基本公式,这些公式随着三角学的诞生而诞生,有着十分悠久的历史。
三角学的数学史
打开20世纪中叶以前的任何一部西方三角学著作,我们都能看到这些公式中至少有一个是用几何方法推导证明的。
通常先研究问题的特殊性,
再扩展到一般性的研究。
在最早时期,三角和的公式
是基于两个锐角来进行研究。
引入:
用两个或者四个全等的三角板
回想勾股定理的证明
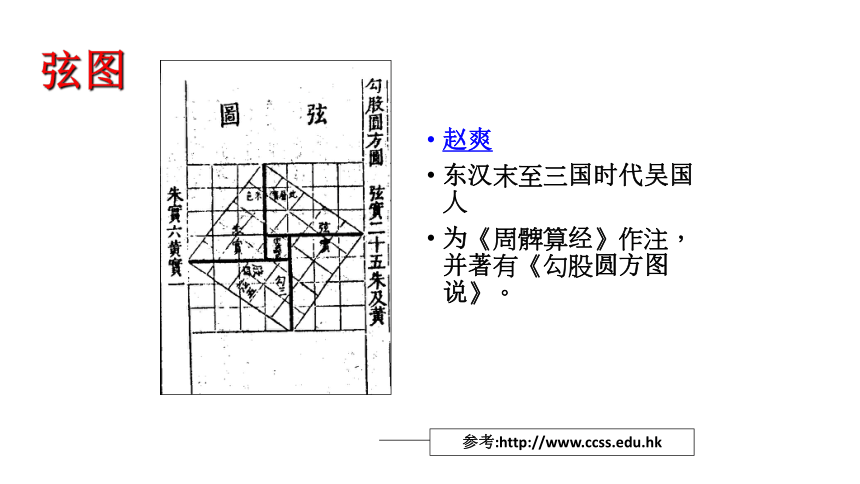
弦图
赵爽
东汉末至三国时代吴国人
为《周髀算经》作注,并著有《勾股圆方图说》。
参考:http://www.ccss.edu.hk
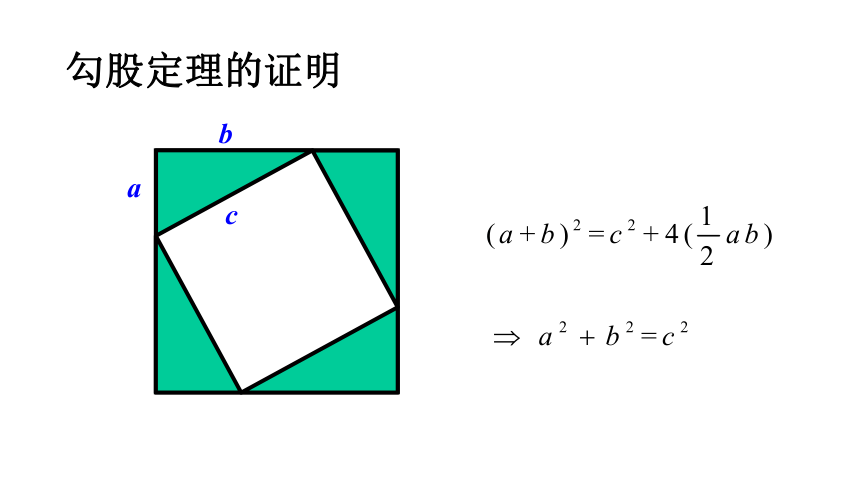
b
a
c
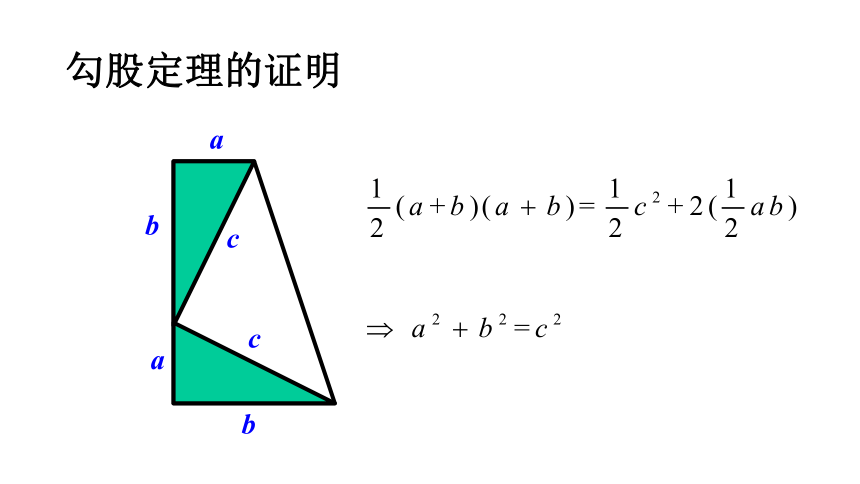
勾股定理的证明
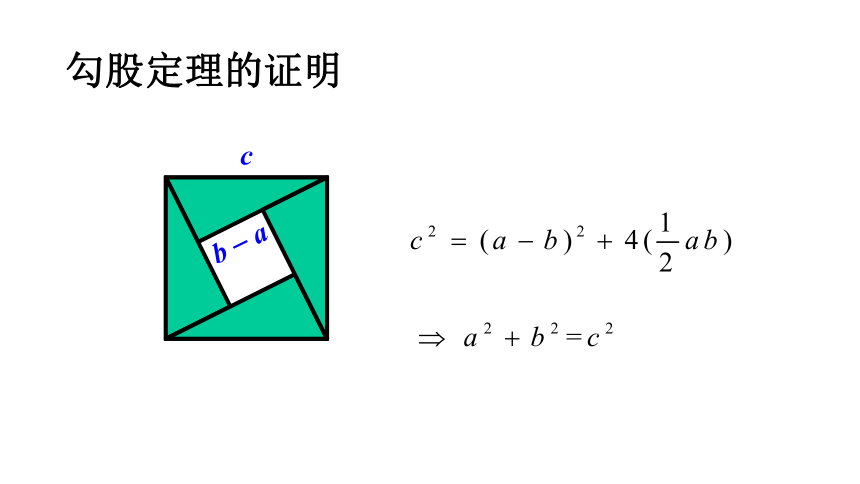
c
b
?
a
勾股定理的证明
a
a
b
b
c
c
勾股定理的证明
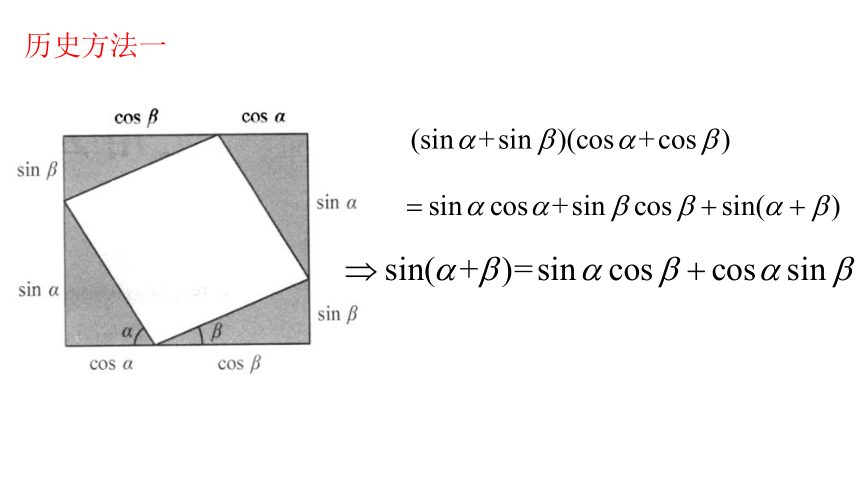
历史方法一
历史方法一
历史方法一
19世纪法国数学家萨吕斯(1798-1866)在《纯粹与应用数学年刊》发表论文。
在单位圆中,利用弦长证明。
历史方法二
探究:对于任意两个角
是否成立?
1941年美国数学家麦克肖恩在《美国数学月刊》发表论文。
避开弦长公式,直接推导出两角和的余弦展开公式。
两角差的余弦公式推导
设
的终边与单位圆
分别交于点
将
同时旋转角
后交单位圆于
显然
一、两角差的余弦公式推导
思考
如何得到
二、两角和与差的余弦公式
对于任意角
都成立:
此公式叫做两角差的余弦公式.
此公式叫做两角和的余弦公式.
两角和与差的正弦公式的推导
替换
,得:
两角和与差的正弦公式
对于任意角
都成立:
此公式叫做两角和的正弦公式.
此公式叫做两角差的正弦公式.
两角和与差的正余弦展开公式
最基本的四组恒等式
解:
例1.
解:
例1.
解:
例2.已知
是锐角,求
的值.
小结
1、HPM是Hisory
and
Pedagogy
of
Mathematics的缩写。HPM组织源自1972年,隶属于国际数学教育委员会,专门研究数学史和数学教育之间的关系。
3、先是从特殊再到一般的研究思想,类比思想,迭代思想,替换思想。
2、初步了解三角学的两角和与差的正余弦展开公式的由来的历史。
4、培养数学建模,直观想象与逻辑推理能力。
HPM有利于帮助我们加深对数学概念,方法和思想的理解,培养创造性思维能力。
帕普斯(Pappus,
3世纪末)
和角公式
课后拓展1
课后拓展1
18,19世纪,少数三角学著作用托勒密定理,来推到两角和的正余弦展开公式。
四边形ABCD中
课后拓展2
18,19世纪,少数三角学著作用托勒密定理,来推到两角和的正余弦展开公式。
四边形AEBD中
课后拓展2
课后思考习题
基于HPM视角下的两角和正余弦展开公式由来的研究
问题:
思考:
核心问题
已知
的六个三角比的值
求值:
两角和与差的正余弦公式常常被称为平面三角学的基本公式,这些公式随着三角学的诞生而诞生,有着十分悠久的历史。
三角学的数学史
打开20世纪中叶以前的任何一部西方三角学著作,我们都能看到这些公式中至少有一个是用几何方法推导证明的。
通常先研究问题的特殊性,
再扩展到一般性的研究。
在最早时期,三角和的公式
是基于两个锐角来进行研究。
引入:
用两个或者四个全等的三角板
回想勾股定理的证明
弦图
赵爽
东汉末至三国时代吴国人
为《周髀算经》作注,并著有《勾股圆方图说》。
参考:http://www.ccss.edu.hk
b
a
c
勾股定理的证明
c
b
?
a
勾股定理的证明
a
a
b
b
c
c
勾股定理的证明
历史方法一
历史方法一
历史方法一
19世纪法国数学家萨吕斯(1798-1866)在《纯粹与应用数学年刊》发表论文。
在单位圆中,利用弦长证明。
历史方法二
探究:对于任意两个角
是否成立?
1941年美国数学家麦克肖恩在《美国数学月刊》发表论文。
避开弦长公式,直接推导出两角和的余弦展开公式。
两角差的余弦公式推导
设
的终边与单位圆
分别交于点
将
同时旋转角
后交单位圆于
显然
一、两角差的余弦公式推导
思考
如何得到
二、两角和与差的余弦公式
对于任意角
都成立:
此公式叫做两角差的余弦公式.
此公式叫做两角和的余弦公式.
两角和与差的正弦公式的推导
替换
,得:
两角和与差的正弦公式
对于任意角
都成立:
此公式叫做两角和的正弦公式.
此公式叫做两角差的正弦公式.
两角和与差的正余弦展开公式
最基本的四组恒等式
解:
例1.
解:
例1.
解:
例2.已知
是锐角,求
的值.
小结
1、HPM是Hisory
and
Pedagogy
of
Mathematics的缩写。HPM组织源自1972年,隶属于国际数学教育委员会,专门研究数学史和数学教育之间的关系。
3、先是从特殊再到一般的研究思想,类比思想,迭代思想,替换思想。
2、初步了解三角学的两角和与差的正余弦展开公式的由来的历史。
4、培养数学建模,直观想象与逻辑推理能力。
HPM有利于帮助我们加深对数学概念,方法和思想的理解,培养创造性思维能力。
帕普斯(Pappus,
3世纪末)
和角公式
课后拓展1
课后拓展1
18,19世纪,少数三角学著作用托勒密定理,来推到两角和的正余弦展开公式。
四边形ABCD中
课后拓展2
18,19世纪,少数三角学著作用托勒密定理,来推到两角和的正余弦展开公式。
四边形AEBD中
课后拓展2
课后思考习题
