沪教版数学高一下册-6.3.1 函数 y=Asin(ωx φ)的 图像与性质 课件(共19张PPT)
文档属性
| 名称 | 沪教版数学高一下册-6.3.1 函数 y=Asin(ωx φ)的 图像与性质 课件(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-27 00:00:00 | ||
图片预览



文档简介
(共19张PPT)
6.3.1函数
的图象与性质
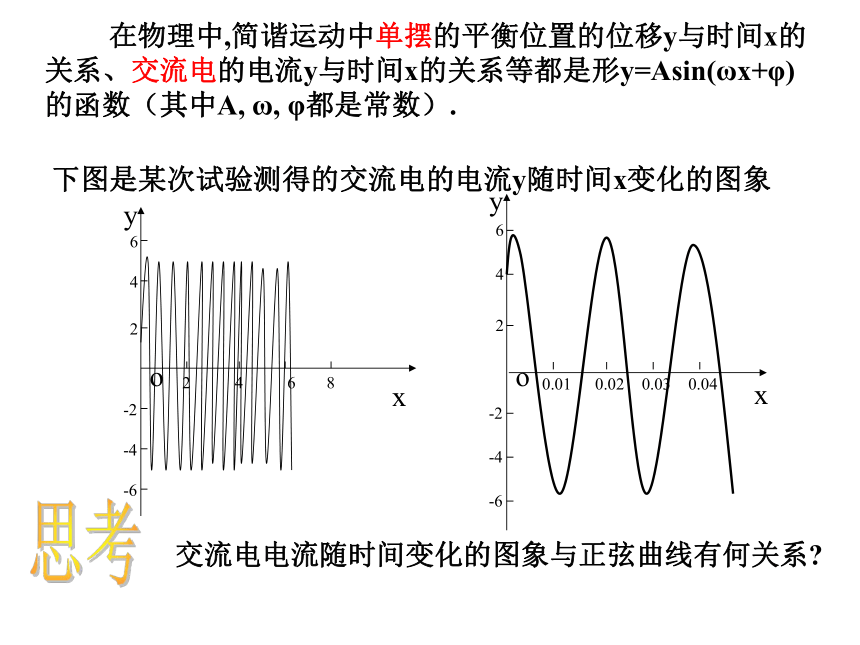
在物理中,简谐运动中单摆的平衡位置的位移y与时间x的关系、交流电的电流y与时间x的关系等都是形y=Asin(ωx+φ)
的函数(其中A,
ω,
φ都是常数).
下图是某次试验测得的交流电的电流y随时间x变化的图象
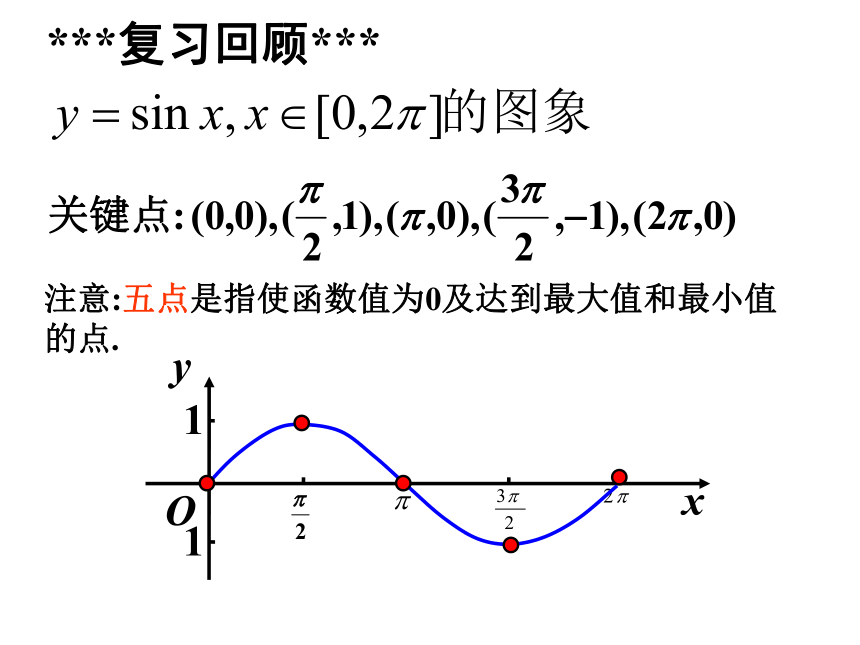
复习回顾
注意:五点是指使函数值为0及达到最大值和最小值的点.
1.y=Asinx与y=sinx的图象关系:
例1:作下列函数图象:
y=sinx
y=sinx
y=Asinx
所有的点纵坐标伸长(A>1)或缩短(0<
A<1)
A倍
横坐标不变
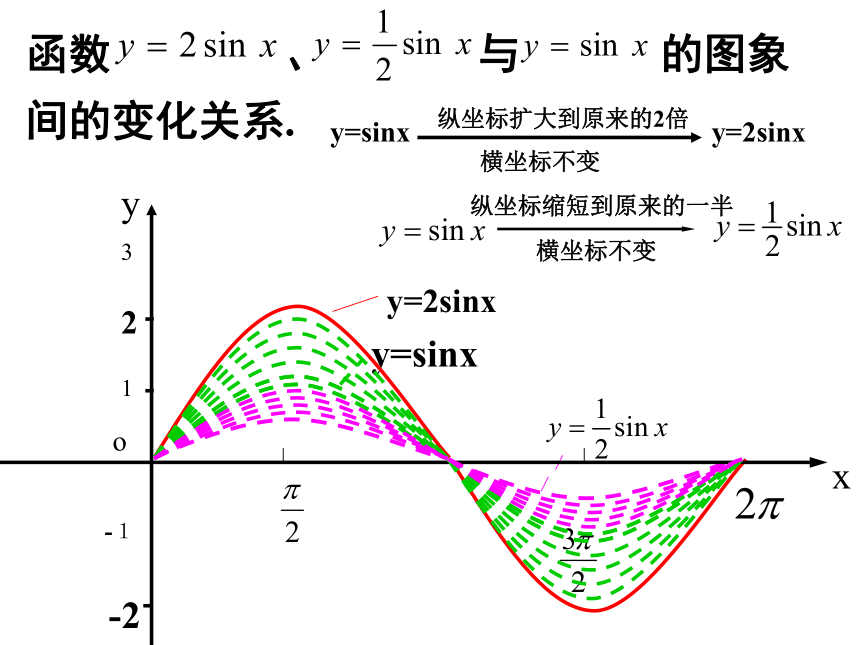
一、函数y=Asinx(A>0)图象:
函数
y=Asinx(A>0且A?1)
的图象可以看作是把y=sinx的图象上所有点的纵坐标伸长(当A>1时)或缩短(当0<
A<1时)到原来的A倍(横坐标不变)而得到的.
A的大小决定这个函数的最大(小)值
y=Asinx,x?R的值域是[-A,
A],
最大值是A,最小值是-A.
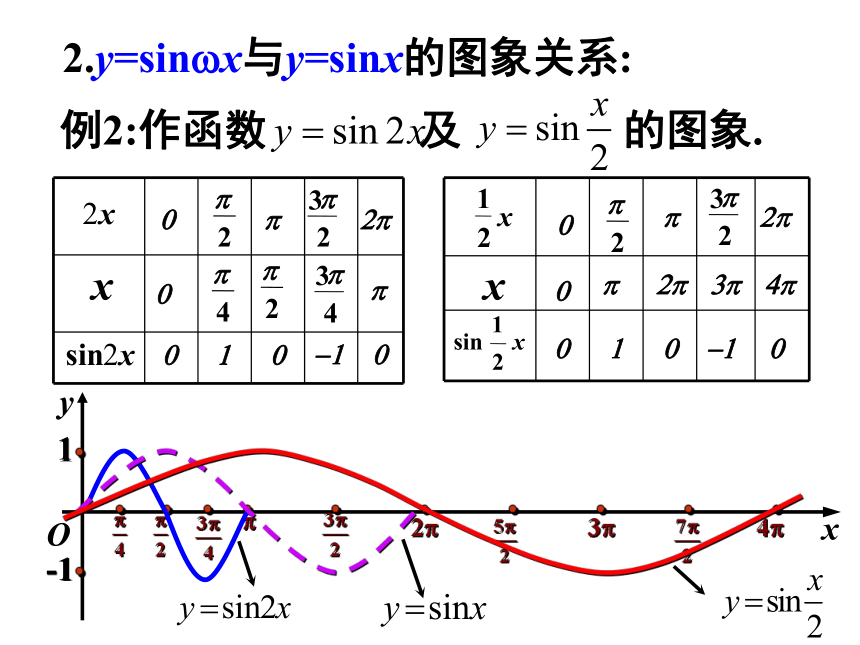
2.y=sin?x与y=sinx的图象关系:
所有的点横坐标缩短(?>1)或伸长(0<
?<1)
1/?倍
二、函数y=sin?x(?>0)图象:
函数
y=sin?x
(?>0且??0)
的图象可以看作是把
y=sinx
的图象上所有点的横坐标缩短(当?>1时)或伸长(当0<
?<1时)到原来的1/?倍(纵坐标不变)而得到的.
y=sinx
y=sin?x
纵坐标不变
?决定函数的周期:
3.y=sin(x+?)与y=sinx的图象关系:
1
-1
所有的点向左(?
>0)
或向右(?
<0)平移
|
?
|
个单位
三、函数y=sin(x+?)图象:
函数
y=sin(x+?)(??0)
的图象可以看作是把y=sinx
的图象上所有的点向左(当?>0时)或向右(当?<0时)平行移动|?|个单位而得到的.
y=sinx
y=sin(x+?)
?的变化引起图象位置发生变化
(左加右减)
平移变换
练习:函数y
=
3cos(x+
)图像向左平移
个单位所得图像的函数表达式为
_____
:先平移后伸缩
:先伸缩后平移
2?
?
y=sinx
y=sin(x+?)
横坐标缩短?>1
(伸长0y=sin(?x+?)
纵坐标伸长A>1
(缩短0y=Asin(?x+?)
y=sinx
y=Asin(?x+?)
总结:
向左?>0
(向右?<0)
平移|?|个单位
纵坐标不变
横坐标不变
y=sinx
横坐标缩短?>1
(伸长0y=sin?x
纵坐标伸长A>1
(缩短0y=Asin(?x+?)
y=sinx
y=Asin(?x+?)
总结:
纵坐标不变
横坐标不变
向左?>0
(向右?<0)
平移|?|/?个单位
参数
的几何意义
例
1、
当函数
y
=
5sin
(2x
--π/4)
表示一个振动量时其振幅为
周期为
______
频率为
相位为
初相为
;
2、将函数
y=
sin2x
的图象向左平移
π/
6
得到的曲线对应的解析式为(
)
A.
y=sin(2x+π/6)
B.
y=sin(2x-π/6)
C.
y=sin(2x+π/3)
D.
y=sin(2x-π/3)
3、要得到函数
y
=
cos3x
的图象,只需将函数
y
=
cos
(3x-π/
6)
的图象(
)
A.
向左平移π/6个单位
B.
向右平移π/6个单位
C.
向左平移π/18个单位
D.
向右平移π/18个单位
4、函数
y
=
3sin(
x/
2
+
π/3)
的图象可由函数
y
=
3
sin
x
经(
)变换而得;
A.????先把横坐标扩大到原来的两倍(纵坐标不变)
,再向左平移π/6个单位
B.???先把横坐标缩短到原来的1/2倍(纵坐标不变)
,再向右平移π/3个单位
C.???先向右平移π/3个单位
,再把横坐标缩短到原来的1/2倍(纵坐标不变)
D.???
先向左平移π/3个单位
,再把横坐标扩大到原来的两倍(纵坐标不变)
5、要得到函数
y
=
cos
(
2x
-π/4)
的图象,只需将函数
y
=
sin
2
x
的图象(
)
A.
向左平移π/4个单位
B.
向右平移π
/
4
个单位
C.
向左平移π/
8个单位
D.
向右平移π/
8个单位
5
π
1/
π
2x
-π/4
-π/
4
C
C
D
D
6.3.1函数
的图象与性质
在物理中,简谐运动中单摆的平衡位置的位移y与时间x的关系、交流电的电流y与时间x的关系等都是形y=Asin(ωx+φ)
的函数(其中A,
ω,
φ都是常数).
下图是某次试验测得的交流电的电流y随时间x变化的图象
复习回顾
注意:五点是指使函数值为0及达到最大值和最小值的点.
1.y=Asinx与y=sinx的图象关系:
例1:作下列函数图象:
y=sinx
y=sinx
y=Asinx
所有的点纵坐标伸长(A>1)或缩短(0<
A<1)
A倍
横坐标不变
一、函数y=Asinx(A>0)图象:
函数
y=Asinx(A>0且A?1)
的图象可以看作是把y=sinx的图象上所有点的纵坐标伸长(当A>1时)或缩短(当0<
A<1时)到原来的A倍(横坐标不变)而得到的.
A的大小决定这个函数的最大(小)值
y=Asinx,x?R的值域是[-A,
A],
最大值是A,最小值是-A.
2.y=sin?x与y=sinx的图象关系:
所有的点横坐标缩短(?>1)或伸长(0<
?<1)
1/?倍
二、函数y=sin?x(?>0)图象:
函数
y=sin?x
(?>0且??0)
的图象可以看作是把
y=sinx
的图象上所有点的横坐标缩短(当?>1时)或伸长(当0<
?<1时)到原来的1/?倍(纵坐标不变)而得到的.
y=sinx
y=sin?x
纵坐标不变
?决定函数的周期:
3.y=sin(x+?)与y=sinx的图象关系:
1
-1
所有的点向左(?
>0)
或向右(?
<0)平移
|
?
|
个单位
三、函数y=sin(x+?)图象:
函数
y=sin(x+?)(??0)
的图象可以看作是把y=sinx
的图象上所有的点向左(当?>0时)或向右(当?<0时)平行移动|?|个单位而得到的.
y=sinx
y=sin(x+?)
?的变化引起图象位置发生变化
(左加右减)
平移变换
练习:函数y
=
3cos(x+
)图像向左平移
个单位所得图像的函数表达式为
_____
:先平移后伸缩
:先伸缩后平移
2?
?
y=sinx
y=sin(x+?)
横坐标缩短?>1
(伸长0y=sin(?x+?)
纵坐标伸长A>1
(缩短0
y=sinx
y=Asin(?x+?)
总结:
向左?>0
(向右?<0)
平移|?|个单位
纵坐标不变
横坐标不变
y=sinx
横坐标缩短?>1
(伸长0y=sin?x
纵坐标伸长A>1
(缩短0
y=sinx
y=Asin(?x+?)
总结:
纵坐标不变
横坐标不变
向左?>0
(向右?<0)
平移|?|/?个单位
参数
的几何意义
例
1、
当函数
y
=
5sin
(2x
--π/4)
表示一个振动量时其振幅为
周期为
______
频率为
相位为
初相为
;
2、将函数
y=
sin2x
的图象向左平移
π/
6
得到的曲线对应的解析式为(
)
A.
y=sin(2x+π/6)
B.
y=sin(2x-π/6)
C.
y=sin(2x+π/3)
D.
y=sin(2x-π/3)
3、要得到函数
y
=
cos3x
的图象,只需将函数
y
=
cos
(3x-π/
6)
的图象(
)
A.
向左平移π/6个单位
B.
向右平移π/6个单位
C.
向左平移π/18个单位
D.
向右平移π/18个单位
4、函数
y
=
3sin(
x/
2
+
π/3)
的图象可由函数
y
=
3
sin
x
经(
)变换而得;
A.????先把横坐标扩大到原来的两倍(纵坐标不变)
,再向左平移π/6个单位
B.???先把横坐标缩短到原来的1/2倍(纵坐标不变)
,再向右平移π/3个单位
C.???先向右平移π/3个单位
,再把横坐标缩短到原来的1/2倍(纵坐标不变)
D.???
先向左平移π/3个单位
,再把横坐标扩大到原来的两倍(纵坐标不变)
5、要得到函数
y
=
cos
(
2x
-π/4)
的图象,只需将函数
y
=
sin
2
x
的图象(
)
A.
向左平移π/4个单位
B.
向右平移π
/
4
个单位
C.
向左平移π/
8个单位
D.
向右平移π/
8个单位
5
π
1/
π
2x
-π/4
-π/
4
C
C
D
D
