人教版八年级下册数学第17章勾股定理复习课件 (共22张PPT)
文档属性
| 名称 | 人教版八年级下册数学第17章勾股定理复习课件 (共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 763.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-27 00:00:00 | ||
图片预览





文档简介
(共22张PPT)
勾股定理复习
1、进一步理解掌握勾股定理及它的逆定理,巩固勾股定理的证明方法。
2、能运用勾股定理和它的逆定理解决一些实际问题。在解决问题的过程中体会如何将实际问题转化为数学问题。
3、记住几组常见的勾股数。
学习目标:
教学过程
理论应用
知识点
习题
习题
知识点
边讲边练
讲练结合
勾股定理
勾股定理逆定理
教学过程
数学思想应用
知识点
习题
习题
知识点
边讲边练
讲练结合
分类思想
方程思想
折叠
截面问题
勾股定理复习
一、知识要点
如果直角三角形两直角边分别为a,b,斜边为c,
那么
勾股定理
a2
+
b2
=
c2
即直角三角形两直角边的平方和等于斜边的平方.
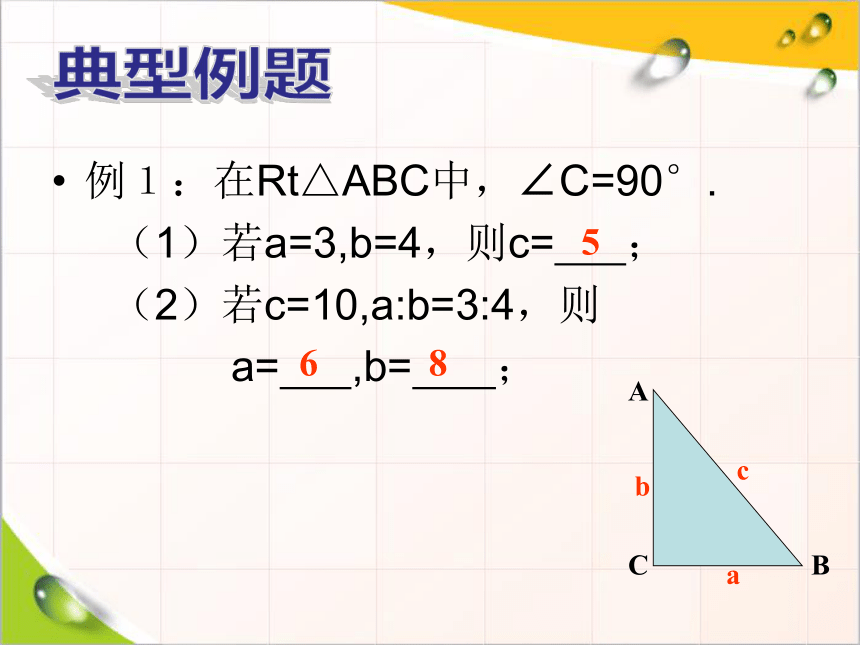
例1:在Rt△ABC中,∠C=90°.
(1)若a=3,b=4,则c=
;
(2)若c=10,a:b=3:4,则
a=
,b=
;
典型例题
5
6
8
A
B
C
a
b
c
勾股逆定理
如果三角形的三边长a,b,c满足
a2
+b2=c2
,
那么这个三角形是直角三角形
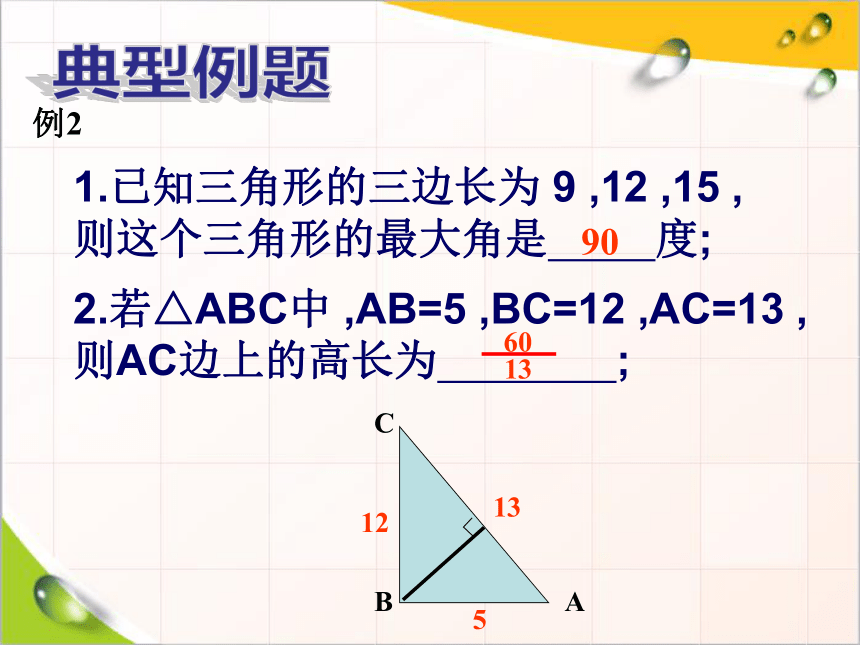
1.已知三角形的三边长为
9
,12
,15
,则这个三角形的最大角是
度;
2.若△ABC中
,AB=5
,BC=12
,AC=13
,则AC边上的高长为
;
例2
90
60
13
典型例题
A
C
5
12
13
B
∟
例4
.观察下列表格:
……
列举
猜想
3、4、5
32=4+5
5、12、13
52=12+13
7、24、25
72=24+25
……
……
13、b、c
132=b+c
请你结合该表格及相关知识,求出b、c的值.
即b=
,c=________
84
85
专题一
分类思想
1.直角三角形中,已知两边长是直角边、斜边不知道时,应分类讨论。
2.当已知条件中没有给出图形时,应认真读句画图,避免遗漏另一种情况。
2.三角形ABC中,AB=10,AC=17,BC边上的高线AD=8,求BC
∟
D
∟
D
A
B
C
1.已知:直角三角形的三边长分别是
3,4,X,则X=
5
或
A
B
C
10
17
8
17
10
8
专题二
方程思想
直角三角形中,当无法已知两边求第三边时,应采用间接求法:灵活地寻找题中的等量关系,利用勾股定理列方程。
1.小东拿着一根长竹竿进一个宽为3米的城门,他先横拿着进不去,又竖起来拿,结果竹竿比城门高1米,当他把竹竿斜着时,两端刚好顶着城门的对角,问竹竿长多少?
x
1m
(x+1)
3
练习
x
专题三
折叠
折叠和轴对称密不可分,利用折叠前后图形全等,找到对应边、对应角相等便可顺利解决折叠问题。
例1、如图,一块直角三角形的纸片,两直角边AC=6㎝,BC=8㎝。现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,求CD的长.
A
C
D
B
E
第8题图
D
x
6
x
8-x
4
6
8
例2:折叠矩形ABCD的一边AD,点D落在BC边上的点F处,已知AB=8CM,BC=10CM,求线段CF
和线段EC的长.
A
B
C
D
E
F
8
10
10
X
8-X
4
8-X
6
1.
几何体的内部路径最值的问题,一般画出几何体截面
2.利用两点之间线段最短,及勾股定理求解。
专题四
截面中的勾股定理
小明家住在18层的高楼,一天,他与妈妈去买竹竿。
买最长的吧!
快点回家,好用它凉衣服。
糟糕,太长了,放不进去。
如果电梯的长、宽、高分别是1米、1米、3米,那么,能放入电梯内的竹竿的最大长度大约是多少米?你能估计出小明买的竹竿至少是多少米吗?(保留整数)
1米
1米
3米
1米
1米
x
x
3米
A
B
C
X2=12+12=2
AB2=32+X2=11
AB≈3米
一种盛饮料的圆柱形杯,测得内部底面半径为2.5㎝,高为12㎝,吸管放进杯里,杯口外面至少要露出4.6㎝,问吸管要做多长?
练习
再
见
勾股定理复习
1、进一步理解掌握勾股定理及它的逆定理,巩固勾股定理的证明方法。
2、能运用勾股定理和它的逆定理解决一些实际问题。在解决问题的过程中体会如何将实际问题转化为数学问题。
3、记住几组常见的勾股数。
学习目标:
教学过程
理论应用
知识点
习题
习题
知识点
边讲边练
讲练结合
勾股定理
勾股定理逆定理
教学过程
数学思想应用
知识点
习题
习题
知识点
边讲边练
讲练结合
分类思想
方程思想
折叠
截面问题
勾股定理复习
一、知识要点
如果直角三角形两直角边分别为a,b,斜边为c,
那么
勾股定理
a2
+
b2
=
c2
即直角三角形两直角边的平方和等于斜边的平方.
例1:在Rt△ABC中,∠C=90°.
(1)若a=3,b=4,则c=
;
(2)若c=10,a:b=3:4,则
a=
,b=
;
典型例题
5
6
8
A
B
C
a
b
c
勾股逆定理
如果三角形的三边长a,b,c满足
a2
+b2=c2
,
那么这个三角形是直角三角形
1.已知三角形的三边长为
9
,12
,15
,则这个三角形的最大角是
度;
2.若△ABC中
,AB=5
,BC=12
,AC=13
,则AC边上的高长为
;
例2
90
60
13
典型例题
A
C
5
12
13
B
∟
例4
.观察下列表格:
……
列举
猜想
3、4、5
32=4+5
5、12、13
52=12+13
7、24、25
72=24+25
……
……
13、b、c
132=b+c
请你结合该表格及相关知识,求出b、c的值.
即b=
,c=________
84
85
专题一
分类思想
1.直角三角形中,已知两边长是直角边、斜边不知道时,应分类讨论。
2.当已知条件中没有给出图形时,应认真读句画图,避免遗漏另一种情况。
2.三角形ABC中,AB=10,AC=17,BC边上的高线AD=8,求BC
∟
D
∟
D
A
B
C
1.已知:直角三角形的三边长分别是
3,4,X,则X=
5
或
A
B
C
10
17
8
17
10
8
专题二
方程思想
直角三角形中,当无法已知两边求第三边时,应采用间接求法:灵活地寻找题中的等量关系,利用勾股定理列方程。
1.小东拿着一根长竹竿进一个宽为3米的城门,他先横拿着进不去,又竖起来拿,结果竹竿比城门高1米,当他把竹竿斜着时,两端刚好顶着城门的对角,问竹竿长多少?
x
1m
(x+1)
3
练习
x
专题三
折叠
折叠和轴对称密不可分,利用折叠前后图形全等,找到对应边、对应角相等便可顺利解决折叠问题。
例1、如图,一块直角三角形的纸片,两直角边AC=6㎝,BC=8㎝。现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,求CD的长.
A
C
D
B
E
第8题图
D
x
6
x
8-x
4
6
8
例2:折叠矩形ABCD的一边AD,点D落在BC边上的点F处,已知AB=8CM,BC=10CM,求线段CF
和线段EC的长.
A
B
C
D
E
F
8
10
10
X
8-X
4
8-X
6
1.
几何体的内部路径最值的问题,一般画出几何体截面
2.利用两点之间线段最短,及勾股定理求解。
专题四
截面中的勾股定理
小明家住在18层的高楼,一天,他与妈妈去买竹竿。
买最长的吧!
快点回家,好用它凉衣服。
糟糕,太长了,放不进去。
如果电梯的长、宽、高分别是1米、1米、3米,那么,能放入电梯内的竹竿的最大长度大约是多少米?你能估计出小明买的竹竿至少是多少米吗?(保留整数)
1米
1米
3米
1米
1米
x
x
3米
A
B
C
X2=12+12=2
AB2=32+X2=11
AB≈3米
一种盛饮料的圆柱形杯,测得内部底面半径为2.5㎝,高为12㎝,吸管放进杯里,杯口外面至少要露出4.6㎝,问吸管要做多长?
练习
再
见
