人教版八年级下册数学17.1勾股定理课件(共30张PPT)
文档属性
| 名称 | 人教版八年级下册数学17.1勾股定理课件(共30张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-27 00:00:00 | ||
图片预览




文档简介
(共30张PPT)
勾
股
定
理
——数形结合之美
人教版
八年级数学(上册)
这个会徽的设计基础是1700多年前,中国古代数学家赵爽的弦图,是为了证明勾股定理而绘制的。经过设计变化成为含义丰富的2002年国际数学家大会的会标。
相传2500年前,毕达哥拉斯有一次在朋友家里做客时,发现朋友家用砖铺成的地面图案反映了直角三角形三边的某种数量关系.
我们也来观察右图中的地面,看看有什么发现?
C
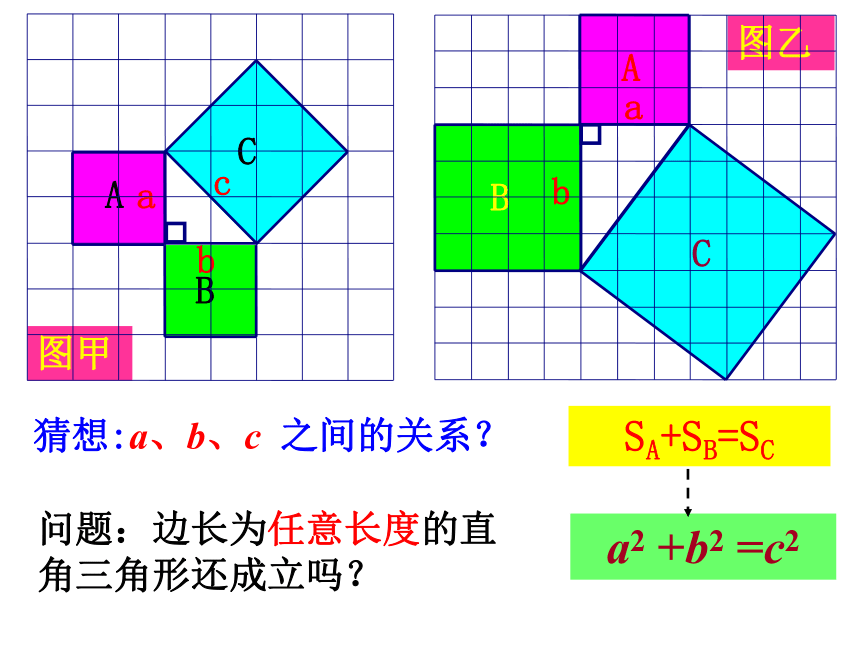
填表:若小方格的边长为1.
图甲
思考:正方形A、B、C的面积有什么关系?
4
4
8
9
16
25
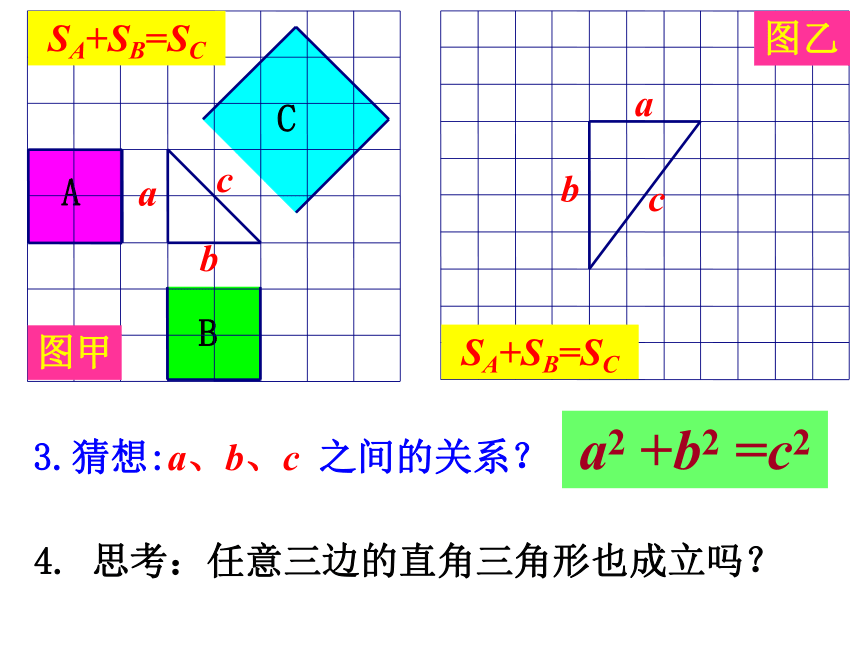
SA+SB=SC
图甲
图乙
A的面积
B的面积
C的面积
图乙
SA+SB=SC
图甲
a
b
c
a
b
c
猜想:a、b、c
之间的关系?
a2
+b2
=c2
问题:边长为任意长度的直角三角形还成立吗?
3.猜想:a、b、c
之间的关系?
a2
+b2
=c2
4.
思考:任意三边的直角三角形也成立吗?
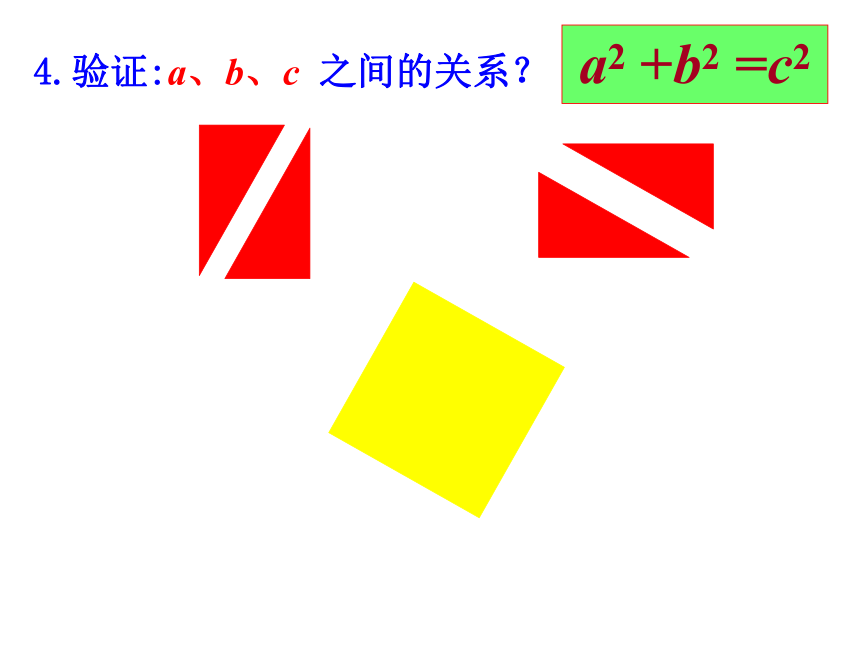
a
用拼图法证明
b
c
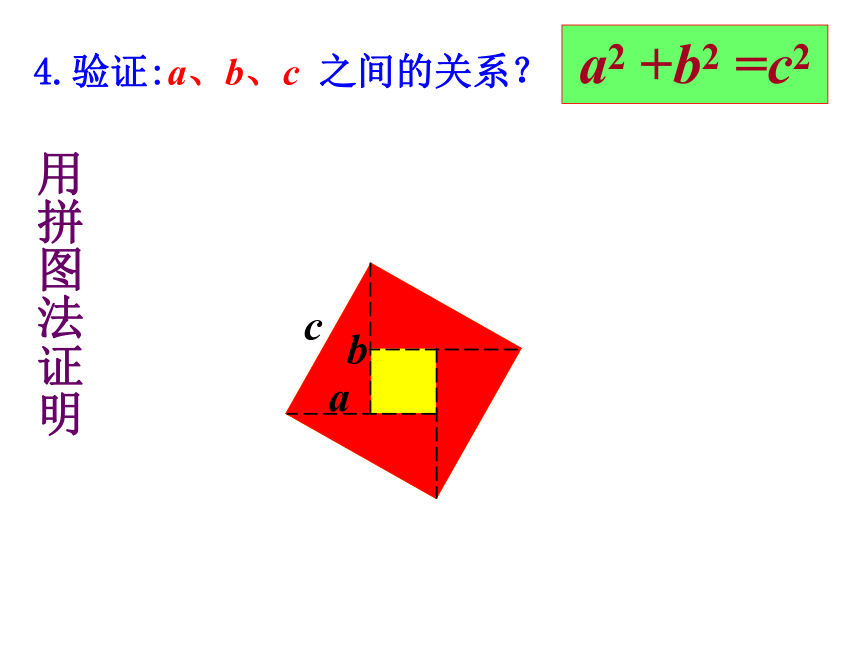
用拼图法证明
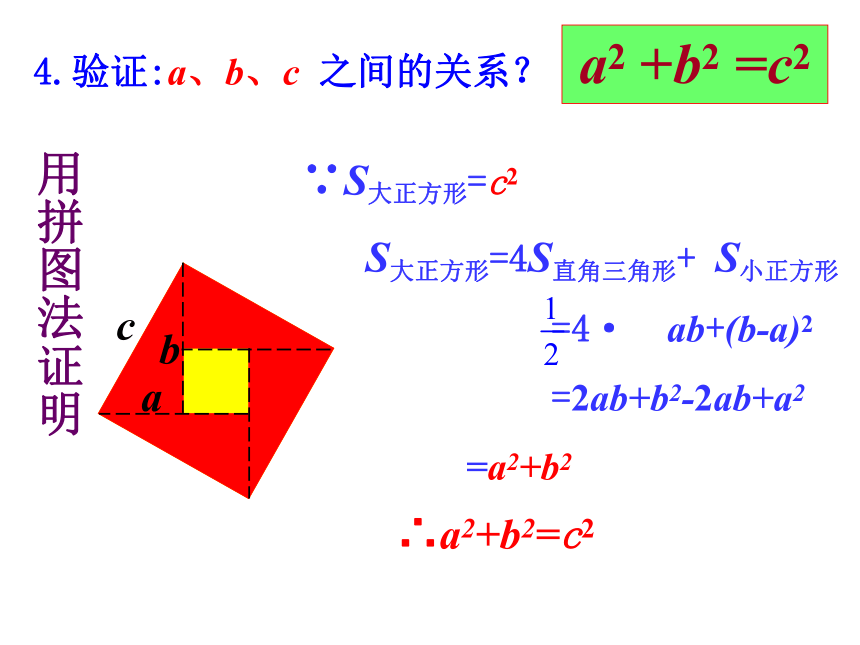
∵S大正方形=c2
S大正方形=4S直角三角形+
S小正方形
=4·
ab+(b-a)2
=2ab+b2-2ab+a2
=a2+b2
用拼图法证明
∴a2+b2=c2
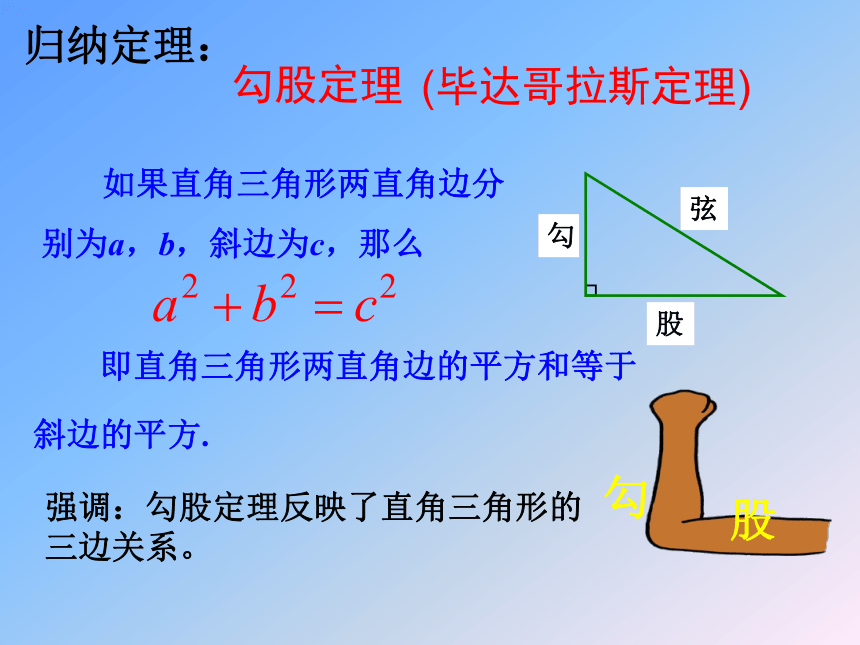
勾股定理
如果直角三角形两直角边分别为a,b,斜边为c,那么
a
c
勾
弦
b
股
归纳定理:
强调:勾股定理反映了直角三角形的三边关系。
(毕达哥拉斯定理)
c2=a2
+b2
a
b
c
确定斜边
b2=
c2
-
a2
a2=
c2
-
b2
a2+b2
=
c2
灵活运用公式
?
变式运用:
a2+c2
=
b2
b2+c2
=
a2
例:在Rt△ABC中,∠C=90°.
(1)
已知:a=6,b=8,求c;
(2)
已知:a=40,c=41,求b;
(3)
已知:c=13,b=5,求a;
(4)
已知:
a:b=3:4,
c=15,求a、b.
例题分析
在直角三角形中,已知两边,可求第三边;
方法小结
∵∠DAB=90?
∴在Rt△ABD中,
BD2=AD2+AB2
=32+42
=25
∴
BD=5
同理可得
DC=13
解:
运用勾股定理
可解决直角三角形中边的计算或证明
已知:四边形ABCD中,∠DAB=∠DBC=90?
AD=3,AB=4,BC=12
求:DC的长。
例2
1、已知:Rt△ABC中,AB=4,AC=3,则BC的长为
.
2、如下图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长是7cm,求正方形A、B、C、D的面积之和。
1、一个门框尺寸如下图所示.
①若有一块长3米,宽0.8米的薄木板,能否通过此门?
②若薄木板长3米,宽1.5米呢?
③若薄木板长3米,宽2.2米呢?为什么?
对角线=
∴能通过此门.
应用知识回归生活
探究:生活中的数学问题
2、小明的妈妈买了一部29英寸(74厘米)的电视机。小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了。你能解释这是为什么吗?
∴售货员没搞错
∵
想一想
荧屏对角线大约为74厘米
我知道了…
…
我感受了…
…
我探索了…
…
c2=a2+b2
两千多年前,古希腊有个哥拉
斯学派,他们首先发现了勾股定理,因此
在国外人们通常称勾股定理为毕达哥拉斯
年希腊曾经发行了一枚纪念票。
定理。为了纪念毕达哥拉斯学派,1955
勾
股
史
话
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前
两千多年前,古希腊有个毕达哥拉斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派,1955年希腊曾经发行了一枚纪念邮票。
国家之一。早在三千多年前
我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。比毕达哥拉斯要早了五百多年。
勾股定理是几何学中的明珠,所以它充满魅力,千百年来,1940年出版过一本名为《毕达哥拉斯命题》的勾股定理的证明专辑,其中收集了367种不同的证明方法。这是任何定理无法比拟的。勾股定理是人类最伟大的十个科学发现之一
。
一、总统证法
a
a
b
b
c
c
美国第20任总统-伽菲尔德
二、出入相补
刘徽(生于公元三世纪)
三國魏晋时代人。
魏景元四年(即
263
年)为古籍《九章算术》作注释。
在注作中,提出以「出入相补」的原理来证明「勾股定理」。后人称该图为「青朱入出图」。
黄色部分面积为a2
绿色部分面积为b2
边长为c
1972年发射的星际飞船“先锋10号”带着这张《青朱入出图》飞向太空,成为与外星人勾通的符号。
数学来源于生活,
服务于生活!
2、查阅有关勾股定理的历史资料,及证明方法,与同学交流。
1、课堂作业:
课本56页,第1、2题;
勾
股
定
理
——数形结合之美
人教版
八年级数学(上册)
这个会徽的设计基础是1700多年前,中国古代数学家赵爽的弦图,是为了证明勾股定理而绘制的。经过设计变化成为含义丰富的2002年国际数学家大会的会标。
相传2500年前,毕达哥拉斯有一次在朋友家里做客时,发现朋友家用砖铺成的地面图案反映了直角三角形三边的某种数量关系.
我们也来观察右图中的地面,看看有什么发现?
C
填表:若小方格的边长为1.
图甲
思考:正方形A、B、C的面积有什么关系?
4
4
8
9
16
25
SA+SB=SC
图甲
图乙
A的面积
B的面积
C的面积
图乙
SA+SB=SC
图甲
a
b
c
a
b
c
猜想:a、b、c
之间的关系?
a2
+b2
=c2
问题:边长为任意长度的直角三角形还成立吗?
3.猜想:a、b、c
之间的关系?
a2
+b2
=c2
4.
思考:任意三边的直角三角形也成立吗?
a
用拼图法证明
b
c
用拼图法证明
∵S大正方形=c2
S大正方形=4S直角三角形+
S小正方形
=4·
ab+(b-a)2
=2ab+b2-2ab+a2
=a2+b2
用拼图法证明
∴a2+b2=c2
勾股定理
如果直角三角形两直角边分别为a,b,斜边为c,那么
a
c
勾
弦
b
股
归纳定理:
强调:勾股定理反映了直角三角形的三边关系。
(毕达哥拉斯定理)
c2=a2
+b2
a
b
c
确定斜边
b2=
c2
-
a2
a2=
c2
-
b2
a2+b2
=
c2
灵活运用公式
?
变式运用:
a2+c2
=
b2
b2+c2
=
a2
例:在Rt△ABC中,∠C=90°.
(1)
已知:a=6,b=8,求c;
(2)
已知:a=40,c=41,求b;
(3)
已知:c=13,b=5,求a;
(4)
已知:
a:b=3:4,
c=15,求a、b.
例题分析
在直角三角形中,已知两边,可求第三边;
方法小结
∵∠DAB=90?
∴在Rt△ABD中,
BD2=AD2+AB2
=32+42
=25
∴
BD=5
同理可得
DC=13
解:
运用勾股定理
可解决直角三角形中边的计算或证明
已知:四边形ABCD中,∠DAB=∠DBC=90?
AD=3,AB=4,BC=12
求:DC的长。
例2
1、已知:Rt△ABC中,AB=4,AC=3,则BC的长为
.
2、如下图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长是7cm,求正方形A、B、C、D的面积之和。
1、一个门框尺寸如下图所示.
①若有一块长3米,宽0.8米的薄木板,能否通过此门?
②若薄木板长3米,宽1.5米呢?
③若薄木板长3米,宽2.2米呢?为什么?
对角线=
∴能通过此门.
应用知识回归生活
探究:生活中的数学问题
2、小明的妈妈买了一部29英寸(74厘米)的电视机。小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了。你能解释这是为什么吗?
∴售货员没搞错
∵
想一想
荧屏对角线大约为74厘米
我知道了…
…
我感受了…
…
我探索了…
…
c2=a2+b2
两千多年前,古希腊有个哥拉
斯学派,他们首先发现了勾股定理,因此
在国外人们通常称勾股定理为毕达哥拉斯
年希腊曾经发行了一枚纪念票。
定理。为了纪念毕达哥拉斯学派,1955
勾
股
史
话
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前
两千多年前,古希腊有个毕达哥拉斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派,1955年希腊曾经发行了一枚纪念邮票。
国家之一。早在三千多年前
我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。比毕达哥拉斯要早了五百多年。
勾股定理是几何学中的明珠,所以它充满魅力,千百年来,1940年出版过一本名为《毕达哥拉斯命题》的勾股定理的证明专辑,其中收集了367种不同的证明方法。这是任何定理无法比拟的。勾股定理是人类最伟大的十个科学发现之一
。
一、总统证法
a
a
b
b
c
c
美国第20任总统-伽菲尔德
二、出入相补
刘徽(生于公元三世纪)
三國魏晋时代人。
魏景元四年(即
263
年)为古籍《九章算术》作注释。
在注作中,提出以「出入相补」的原理来证明「勾股定理」。后人称该图为「青朱入出图」。
黄色部分面积为a2
绿色部分面积为b2
边长为c
1972年发射的星际飞船“先锋10号”带着这张《青朱入出图》飞向太空,成为与外星人勾通的符号。
数学来源于生活,
服务于生活!
2、查阅有关勾股定理的历史资料,及证明方法,与同学交流。
1、课堂作业:
课本56页,第1、2题;
