人教A版高中数学必修三第二章第3节 2.3.2两个变量的线性相关 课件(共28张PPT)
文档属性
| 名称 | 人教A版高中数学必修三第二章第3节 2.3.2两个变量的线性相关 课件(共28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 676.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-27 10:46:42 | ||
图片预览








文档简介
(共28张PPT)
2.3.2
两个变量的线性相关
【学法指导】
在解决统计问题的过程中,系统地经历数据收集和处理的全过程,进一步体会用样本估计总体的思想,理解数形结合的数学思想和回归分析的统计思想。
【学习目标】
1、理解线性相关、正相关、负相关、散点图;
2、理清线性相关和散点图之间的关系;(定性)
3、在两个变量具有线性相关关系时,会作出线性直线。(定量)
【创设情境
复习导入】
相关关系:自变量取值一定时,因变量的取值不确定,它按某种规律在一定范围内变化.即带有一定随机性的变量关系.
函数关系:自变量取值一定时,因变量的取值是确定的关系。如y=2x+1,y=sinx
判断下面两个变量分别是什么关系
(1)喜鹊叫,好事到。
(2)心情好,学习效率高。
(3)喜鹊叫,高考考得好。
应当说,对于上述各种问题中的两个变量之间的相关关系,我们都可以根据自己的生活、学习经验作出相应的判断,因为“经验当中有规律”。但是,不管你经验多么丰富如果只凭经验办事,还是很容易出错的。因此,在分析两个变量之间的关系时,我们还需要有一些有说服力的方法。
在现实生活中存在着大量的相关关系,如何判断和描述相关关系,统计学发挥着非常重要的作用.变量之间的相关关系带有不确定性,这需要通过收集大量的数据,对数据进行统计分析,发现规律,才能作出科学的判断.(对具有相关关系的两个变量进行统计分析的方法叫回归分析.)
.
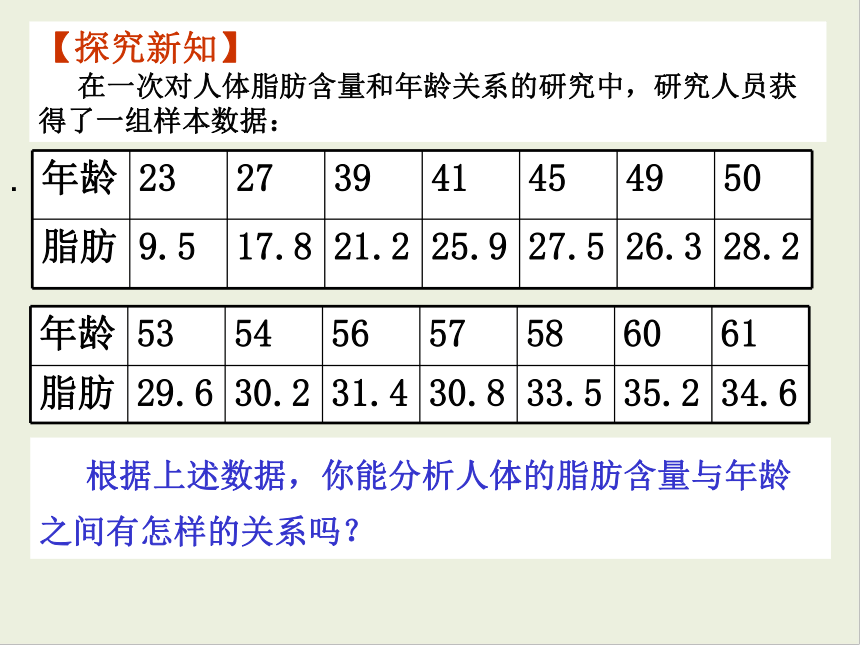
根据上述数据,你能分析人体的脂肪含量与年龄之间有怎样的关系吗?
【探究新知】
在一次对人体脂肪含量和年龄关系的研究中,研究人员获得了一组样本数据:
年龄
23
27
39
41
45
49
50
脂肪
9.5
17.8
21.2
25.9
27.5
26.3
28.2
年龄
53
54
56
57
58
60
61
脂肪
29.6
30.2
31.4
30.8
33.5
35.2
34.6
探究一
收集数据
(1)回忆前面学过的统计知识,表中数据可能是如何收集到的?举例说明
(2)如何理解23岁对应的脂肪百分比为9.5?
探究二
分析数据
(1)统计学中常用什么方法分析收集到的数据?
(2)高一在函数应用章节,如何根据已知数据预测其它数据?
(3)你发现年龄与脂肪含量这两个变量之间是什么关系?怎样发现的?
探究三
寻找回归直线(定量)
(1)回归直线一定过样本点的中心吗?为什么?
(2)为什么要找回归直线?找到这条直线是否说明年龄与脂肪含量是函数关系?
(3)假如我45岁,我的脂肪含量大约是多少?是表中的27.5吗?
(4)如何具体求出这个回归直线的方程呢?回归直线与散点图中各点的位置应具有怎样的关系?
【小组合作】
探究一
收集数据
(1)回忆前面学过的统计知识,表中数据可能是如何收集到的?举例说明
(2)如何理解23岁对应的脂肪百分比为9.5?
【展示交流】
探究二
分析数据
(1)统计学中常用什么方法分析收集到的数据?
(2)高一在函数应用章节,如何根据已知数据预测其它数据?
(3)你发现年龄与脂肪含量这两个变量之间是什么关系?怎样发现的?
【展示交流】
人体内脂肪含量与年龄之间是相关关系
在一定年龄段内,随着年龄的增长,人体内的脂肪含量会增加,但人体内的脂肪含量还与饮食习惯、体育锻炼等有关,可能还与个人的先天体质有关。
对某一个人来说,他的体内脂肪含量不一定随年龄
增长而增加或减少,但是如果把很多个体放在一起,就可能表现出一定的规律性.
散点图:
将各数据在平面坐标系中的对应点画出来,得到表示两个变量的一组数据的图形,这样的图形叫做散点图。
如下图:
图中点的趋势表明两个变量之间确实存在一定的关系,年龄越大,体内脂肪含量越高。这个图支持了我们从数据表中得出的结论。
体现了数学思想方法:数形结合!
思考:你能举一些生活
中的变量成正相关或成
负相关的例子吗?
观察点的位置:发现散布在从左下角到右上角的区域。称它们为正相关。但有的两个变量的相关如右图所示成负相关。
正相关
负相关
如何从散点图直观判断两个变量是否有相关关系?
1.如果所有的样本点都落在某一函数曲线上,这两个变量有什么关系?
——具有函数关系.
2.如果所有的样本点都落在某一函数曲线附近,那么这两个变量之间有关系吗?关系确定吗?是什么关系?
——有关系,不确定,有相关关系。
3.
如果所有的样本点都落在某一直线附近,变量之间就有线性相关关系。线性相关又分正相关和负相关。(呈条形状)
4.如果散点图的点几乎没有什么规则,则这两个变量之间关系又如何?
——没有相关关系
探究三
寻找回归直线(定量)
(1)回归直线一定过样本点的中心吗?为什么?
(2)为什么要找回归直线?找到这条直线是否说明年龄与脂肪含量是函数关系?
(3)假如我45岁,我的脂肪含量大约是多少?是表中的27.5吗?
(4)如何具体求出这个回归直线的方程呢?回归直线与散点图中各点的位置应具有怎样的关系?
【展示交流】
观察散点图的特征,如果各点大致分布在一条直线的附近,就称两个变量之间具有线性相关的关系,这条直线叫做回归直线。
只有散点图中的点呈条状集中在某一直线周围,
才可以用回归直线来描述两个变量之间的关系.
建立回归直线的目的,一是为了从整体上代表两个变量的观测数据的关系,这与用平均数来代表一个变量的数据是类似的.二是观测值不可能正好落在回归直线上.(什么情况下才会出现点正好都落在回归直线上?)
回归直线
体现了数学思想方法:类比推理!
EXCEL
体现了数学思想方法:转化与化归思想
回归直线依赖样本数据,依赖对样本数据拟合的效果。因此,回归方程有随机性,由它获得的结论也具有随机性的特点。回归分析就是寻找相关关系中非确定关系中的某种确定性。虽然一个数据具有随机误差,但“总体”具有某种确定的关系.即随机中包含有某种确定性的规律。
EXCEL
求出直线的回归方程的应用:
(1)描述两变量之间的依存关系;利用直线的回归方程即可定量描述两个变量间依存的数量关系
(2)利用回归方程进行预测;把预报因子(即自变量x)代入回归方程对预报量(即因变量Y)进行估计,即可得到个体Y值的容许区间。
(3)利用回归方程进行统计控制规定Y值的变化,通过控制x的范围来实现统计控制的目标。如已经得到了空气中NO2的浓度和汽车流量间的回归方程,即可通过控制汽车流量来控制空气中NO2的浓度。
回归方程
体现了统计思想:
用确定关系来研究不确定的相关关系。
EXCEL
(1)做回归分析要有实际意义;
(2)回归分析前,最好先作出散点图;
(3)回归直线不要外延。
应用回归直线的注意事项:
EXCEL
下面列举了四种可能性,你认为可行吗?
图(1)表示每一点到直线的垂直距离之和最短,图(2)表示每一点到直线的“偏差”之和最短,图(3)表示经过点最多的直线,图(4)表示上下点的个数“大概”一样多的直线.??
体现了数学思想方法:转化与化归思想
回归直线与散点图各点的位置应是:整体上最接近
运算不方便
避免相互抵消
各点与直线
的整体偏差
最小二乘法
【课堂小结】
样本估计总体
数形结合
类比
转化与化归
回归分析
回归分析是用确定的函数关系来研究不确定的相关关系;体会统计思维和确定思维的差异。加深对用样本估计总体思想的理解,感受到统计的力量!
(预测和x对y的影响能力)
相关关系
:因为有关联性,才有研究的必要性.因为其不确定性,从少量的变量观测值,很难估计误差的大小,因此必须对变量作大量的观测.但每个观测值都有一定误差,为了消除误差的影响,揭示变量间的本质联系,就必须要用统计分析方法.------回归分析
本节通过“用线性回归的统计分析方法,刻画两个变量之间的相关关系”的统计案例,一起经历了一个相对完整的统计过程,感受统计与实际生活的联系以及在解决实际问题中的作用。
2.3.2
两个变量的线性相关
【学法指导】
在解决统计问题的过程中,系统地经历数据收集和处理的全过程,进一步体会用样本估计总体的思想,理解数形结合的数学思想和回归分析的统计思想。
【学习目标】
1、理解线性相关、正相关、负相关、散点图;
2、理清线性相关和散点图之间的关系;(定性)
3、在两个变量具有线性相关关系时,会作出线性直线。(定量)
【创设情境
复习导入】
相关关系:自变量取值一定时,因变量的取值不确定,它按某种规律在一定范围内变化.即带有一定随机性的变量关系.
函数关系:自变量取值一定时,因变量的取值是确定的关系。如y=2x+1,y=sinx
判断下面两个变量分别是什么关系
(1)喜鹊叫,好事到。
(2)心情好,学习效率高。
(3)喜鹊叫,高考考得好。
应当说,对于上述各种问题中的两个变量之间的相关关系,我们都可以根据自己的生活、学习经验作出相应的判断,因为“经验当中有规律”。但是,不管你经验多么丰富如果只凭经验办事,还是很容易出错的。因此,在分析两个变量之间的关系时,我们还需要有一些有说服力的方法。
在现实生活中存在着大量的相关关系,如何判断和描述相关关系,统计学发挥着非常重要的作用.变量之间的相关关系带有不确定性,这需要通过收集大量的数据,对数据进行统计分析,发现规律,才能作出科学的判断.(对具有相关关系的两个变量进行统计分析的方法叫回归分析.)
.
根据上述数据,你能分析人体的脂肪含量与年龄之间有怎样的关系吗?
【探究新知】
在一次对人体脂肪含量和年龄关系的研究中,研究人员获得了一组样本数据:
年龄
23
27
39
41
45
49
50
脂肪
9.5
17.8
21.2
25.9
27.5
26.3
28.2
年龄
53
54
56
57
58
60
61
脂肪
29.6
30.2
31.4
30.8
33.5
35.2
34.6
探究一
收集数据
(1)回忆前面学过的统计知识,表中数据可能是如何收集到的?举例说明
(2)如何理解23岁对应的脂肪百分比为9.5?
探究二
分析数据
(1)统计学中常用什么方法分析收集到的数据?
(2)高一在函数应用章节,如何根据已知数据预测其它数据?
(3)你发现年龄与脂肪含量这两个变量之间是什么关系?怎样发现的?
探究三
寻找回归直线(定量)
(1)回归直线一定过样本点的中心吗?为什么?
(2)为什么要找回归直线?找到这条直线是否说明年龄与脂肪含量是函数关系?
(3)假如我45岁,我的脂肪含量大约是多少?是表中的27.5吗?
(4)如何具体求出这个回归直线的方程呢?回归直线与散点图中各点的位置应具有怎样的关系?
【小组合作】
探究一
收集数据
(1)回忆前面学过的统计知识,表中数据可能是如何收集到的?举例说明
(2)如何理解23岁对应的脂肪百分比为9.5?
【展示交流】
探究二
分析数据
(1)统计学中常用什么方法分析收集到的数据?
(2)高一在函数应用章节,如何根据已知数据预测其它数据?
(3)你发现年龄与脂肪含量这两个变量之间是什么关系?怎样发现的?
【展示交流】
人体内脂肪含量与年龄之间是相关关系
在一定年龄段内,随着年龄的增长,人体内的脂肪含量会增加,但人体内的脂肪含量还与饮食习惯、体育锻炼等有关,可能还与个人的先天体质有关。
对某一个人来说,他的体内脂肪含量不一定随年龄
增长而增加或减少,但是如果把很多个体放在一起,就可能表现出一定的规律性.
散点图:
将各数据在平面坐标系中的对应点画出来,得到表示两个变量的一组数据的图形,这样的图形叫做散点图。
如下图:
图中点的趋势表明两个变量之间确实存在一定的关系,年龄越大,体内脂肪含量越高。这个图支持了我们从数据表中得出的结论。
体现了数学思想方法:数形结合!
思考:你能举一些生活
中的变量成正相关或成
负相关的例子吗?
观察点的位置:发现散布在从左下角到右上角的区域。称它们为正相关。但有的两个变量的相关如右图所示成负相关。
正相关
负相关
如何从散点图直观判断两个变量是否有相关关系?
1.如果所有的样本点都落在某一函数曲线上,这两个变量有什么关系?
——具有函数关系.
2.如果所有的样本点都落在某一函数曲线附近,那么这两个变量之间有关系吗?关系确定吗?是什么关系?
——有关系,不确定,有相关关系。
3.
如果所有的样本点都落在某一直线附近,变量之间就有线性相关关系。线性相关又分正相关和负相关。(呈条形状)
4.如果散点图的点几乎没有什么规则,则这两个变量之间关系又如何?
——没有相关关系
探究三
寻找回归直线(定量)
(1)回归直线一定过样本点的中心吗?为什么?
(2)为什么要找回归直线?找到这条直线是否说明年龄与脂肪含量是函数关系?
(3)假如我45岁,我的脂肪含量大约是多少?是表中的27.5吗?
(4)如何具体求出这个回归直线的方程呢?回归直线与散点图中各点的位置应具有怎样的关系?
【展示交流】
观察散点图的特征,如果各点大致分布在一条直线的附近,就称两个变量之间具有线性相关的关系,这条直线叫做回归直线。
只有散点图中的点呈条状集中在某一直线周围,
才可以用回归直线来描述两个变量之间的关系.
建立回归直线的目的,一是为了从整体上代表两个变量的观测数据的关系,这与用平均数来代表一个变量的数据是类似的.二是观测值不可能正好落在回归直线上.(什么情况下才会出现点正好都落在回归直线上?)
回归直线
体现了数学思想方法:类比推理!
EXCEL
体现了数学思想方法:转化与化归思想
回归直线依赖样本数据,依赖对样本数据拟合的效果。因此,回归方程有随机性,由它获得的结论也具有随机性的特点。回归分析就是寻找相关关系中非确定关系中的某种确定性。虽然一个数据具有随机误差,但“总体”具有某种确定的关系.即随机中包含有某种确定性的规律。
EXCEL
求出直线的回归方程的应用:
(1)描述两变量之间的依存关系;利用直线的回归方程即可定量描述两个变量间依存的数量关系
(2)利用回归方程进行预测;把预报因子(即自变量x)代入回归方程对预报量(即因变量Y)进行估计,即可得到个体Y值的容许区间。
(3)利用回归方程进行统计控制规定Y值的变化,通过控制x的范围来实现统计控制的目标。如已经得到了空气中NO2的浓度和汽车流量间的回归方程,即可通过控制汽车流量来控制空气中NO2的浓度。
回归方程
体现了统计思想:
用确定关系来研究不确定的相关关系。
EXCEL
(1)做回归分析要有实际意义;
(2)回归分析前,最好先作出散点图;
(3)回归直线不要外延。
应用回归直线的注意事项:
EXCEL
下面列举了四种可能性,你认为可行吗?
图(1)表示每一点到直线的垂直距离之和最短,图(2)表示每一点到直线的“偏差”之和最短,图(3)表示经过点最多的直线,图(4)表示上下点的个数“大概”一样多的直线.??
体现了数学思想方法:转化与化归思想
回归直线与散点图各点的位置应是:整体上最接近
运算不方便
避免相互抵消
各点与直线
的整体偏差
最小二乘法
【课堂小结】
样本估计总体
数形结合
类比
转化与化归
回归分析
回归分析是用确定的函数关系来研究不确定的相关关系;体会统计思维和确定思维的差异。加深对用样本估计总体思想的理解,感受到统计的力量!
(预测和x对y的影响能力)
相关关系
:因为有关联性,才有研究的必要性.因为其不确定性,从少量的变量观测值,很难估计误差的大小,因此必须对变量作大量的观测.但每个观测值都有一定误差,为了消除误差的影响,揭示变量间的本质联系,就必须要用统计分析方法.------回归分析
本节通过“用线性回归的统计分析方法,刻画两个变量之间的相关关系”的统计案例,一起经历了一个相对完整的统计过程,感受统计与实际生活的联系以及在解决实际问题中的作用。
