北京版八年级下册数学 15.4正方形的判定 课件(86张ppt)
文档属性
| 名称 | 北京版八年级下册数学 15.4正方形的判定 课件(86张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-26 00:00:00 | ||
图片预览











文档简介
(共86张PPT)
初二年级
数学
正方形的判定
我们已经学习了平行四边形,矩形和菱形,它们是如何判定的?
复习回顾
引出课题
平行四边形的判定
两组对边分别平行的四边形
两组对边分别相等的四边形
对角线互相平分的四边形
一组对边平行且相等的四边形
矩形的判定
菱形的判定
有一个角是直角的
平行四边形
对角线相等的
平行四边形
有三个角是直角的四边形
矩形的判定
菱形的判定
有一个角是直角的
平行四边形
一组邻边相等的
平行四边形
对角线相等的
平行四边形
有三个角是直角的四边形
对角线互相垂直的
平行四边形
四边相等的四边形
平行四边形
菱形
一组邻边相等
平行四边形
矩形
有一个角直角
问题:如果平行四边形的边和角一起特殊化,
能得到什么呢?
平行四边形
正方形
一个角是直角
一组邻边相等
正方形的定义:
有一组邻边相等并且有一个角是直角
的平行四边形叫做正方形.
平行四边形
正方形
一个角是直角
一组邻边相等
判定一个四边形是正方形的关键在于
判定它既是菱形又是矩形.
探究猜想
归纳判定
问题:明明在商场中想买一块正方形纱巾,但不知是否
是正方形的,只见售货员阿姨拉起纱巾的一组对
角,能完全重合,重合后变成三角形,在此基础
上,将另两个顶点再对折,也能完全重合.
阿姨
认为这样能够证明是正方形,把纱巾给了明明,
你认为明明手上的纱巾一定是正方形吗?
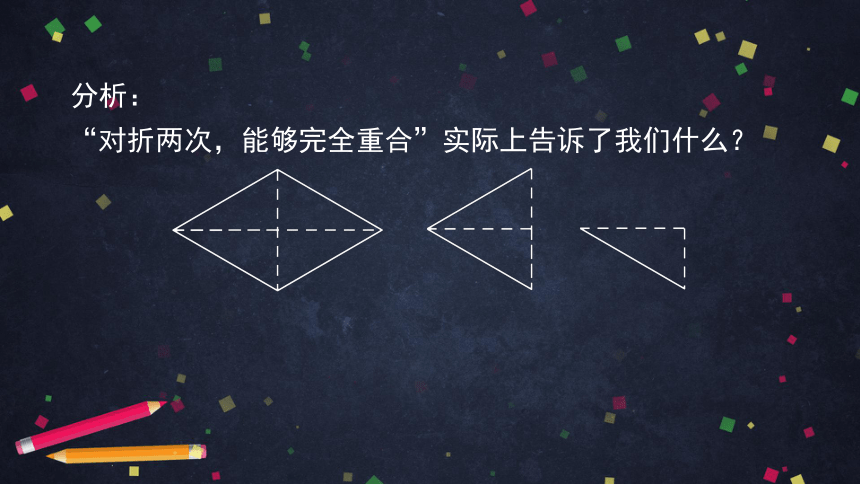
“对折两次,能够完全重合”实际上告诉了我们什么?
分析:
“对折两次,能够完全重合”实际上告诉了我们什么?
分析:
四边相等,对角线互相垂直平分,即纱巾的
两条对角线所在的直线是对称轴.由此我们只
能保证纱巾是菱形.
如果要判断纱巾是正方形,还需要在菱形的基础上判定
它是矩形.因此还需要添加什么条件?
思考:
如果要判断纱巾是正方形,还需要在菱形的基础上判定
它是矩形.因此还需要添加什么条件?
思考:
有一个角是直角.实际上改变菱形的角,
当有一个角是直角时,菱形就变成了正方形.
当有一个角是直角
从对角线来考虑,在菱形的基础上,对角线满足什么条件可以得到正方形?
当对角线相等
?
猜想:对角线相等的菱形是正方形.
分析:平行四边形+对角线相等
矩形
有一个角是直角
已知:四边形ABCD是菱形,AC=BD.
求证:四边形ABCD是正方形.
猜想:对角线相等的菱形是正方形
证明:∵四边形ABCD是菱形,
∴四边形ABCD是平行四边形,
AB=AD.
已知:四边形ABCD是菱形,AC=BD.
求证:四边形ABCD是正方形.
猜想:对角线相等的菱形是正方形
已知:四边形ABCD是菱形,AC=BD.
求证:四边形ABCD是正方形.
证明:∵AC=BD,
∴四边形ABCD是矩形.
∴∠DAB=90°.
∴四边形ABCD是正方形.
(1)在菱形的基础上:
判定有一个角是直角或对角线相等.
符号语言:
∵四边形ABCD是菱形,∠BAD=90°(或AC=BD),
∴四边形ABCD是正方形.
判定有一个角是直角或对角线相等.
(1)在菱形的基础上:
问题:
如果在矩形的基础上判断一个四边形是正方形,
需要添加什么条件?
要使一个矩形成为正方形,还需添加一组邻边相等.
实际上改变矩形的边,当矩形的邻边相等时,矩形
就成为正方形.
当有一组邻边相等
问题:
如果在矩形的基础上判断一个四边形正方形,
需要添加什么条件?
从对角线来考虑,在矩形的基础上,对角线满足什么条件可以得到正方形?
当对角线互相垂直
?
猜想:对角线互相垂直的矩形是正方形.
分析:平行四边形+对角线互相垂直
菱形
有一组邻边相等
已知:四边形ABCD是矩形,AC⊥BD.
求证:四边形ABCD是正方形.
猜想:对角线互相垂直的矩形是正方形.
已知:四边形ABCD是矩形,AC⊥BD.
求证:四边形ABCD是正方形.
证明:∵四边形ABCD是矩形,
∴四边形ABCD是平行四边形,
∠DAB=90°.
证明:∵AC⊥BD,
∴四边形ABCD是菱形.
∴AB=AD.
∴四边形ABCD是正方形.
猜想:对角线互相垂直的矩形是正方形.
已知:四边形ABCD是矩形,AC⊥BD.
求证:四边形ABCD是正方形.
判定有一组邻边相等或者对角线互相
垂直.
(2)在矩形的基础上:
符号语言:
∵四边形ABCD是矩形,BA=BC(或AC⊥BD),
∴四边形ABCD是正方形.
(2)在矩形的基础上:
判定有一组邻边相等或者对角线互相
垂直.
在四边形的基础上,添加什么条件可以得到正方形?
当对角线相等
且互相垂直平分
?
猜想:对角线相等且互相垂直平分的四边形是正方形.
分析:对角线互相平分
平行四边形
已知:在四边形ABCD中,AC=BD,AC⊥BD,
OA=OC,OB=OD.
求证:四边形ABCD是正方形.
平行四边形+对角线垂直
菱形
有一组邻边相等
有一个角是直角
平行四边形+对角线相等
矩形
证明:∵OA=OC,OB=OD,
∴四边形ABCD是平行四边形.
∵AC=BD,
∴四边形ABCD是矩形.
∴∠DAB=90°.
猜想:对角线相等且互相垂直平分的四边形是正方形.
已知:在四边形ABCD中,AC=BD,AC⊥BD,
OA=OC,OB=OD.
求证:四边形ABCD是正方形.
证明:∵AC⊥BD,
∴四边形ABCD是菱形.
∴AB=AD.
∴四边形ABCD是正方形.
猜想:对角线相等且互相垂直平分的四边形是正方形.
已知:在四边形ABCD中,AC=BD,AC⊥BD,
OA=OC,OB=OD.
求证:四边形ABCD是正方形.
判定对角线相等,并且互相垂直平分.
(3)在四边形的基础上:
符号语言:
∵AC=BD,AC⊥BD,AO=CO,BO=DO,
∴四边形ABCD是正方形.
判定对角线相等,并且互相垂直平分.
(3)在四边形的基础上:
问题3:
菱形,矩形,正方形间有怎样的联系?
平行四边形
四边形
从边和角考虑:
两组对边
分别平行
问题3:
菱形,矩形,正方形间有怎样的联系?
平行四边形
四边形
一个角是直角
从边和角考虑:
两组对边
分别平行
矩形
问题3:
菱形,矩形,正方形间有怎样的联系?
平行四边形
四边形
矩形
菱形
一个角是直角
一组邻边相等
从边和角考虑:
两组对边
分别平行
问题3:
菱形,矩形,正方形间有怎样的联系?
平行四边形
四边形
矩形
菱形
正方形
一个角是直角
一组邻边相等
一组邻边相等
从边和角考虑:
两组对边
分别平行
问题3:
菱形,矩形,正方形间有怎样的联系?
平行四边形
四边形
矩形
菱形
正方形
一个角是直角
一组邻边相等
一个角是直角
一组邻边相等
从边和角考虑:
两组对边
分别平行
问题3:
菱形,矩形,正方形间有怎样的联系?
平行四边形
四边形
矩形
菱形
正方形
一个角是直角
一组邻边相等
一个角是直角
一组邻边相等
一个角是直角
一组邻边相等
从边和角考虑:
两组对边
分别平行
问题3:
菱形,矩形,正方形间有怎样的联系?
平行四边形
四边形
从对角线考虑:
对角线
互相平分
问题3:
菱形,矩形,正方形间有怎样的联系?
平行四边形
四边形
矩形
对角线相等
从对角线考虑:
对角线
互相平分
问题3:
菱形,矩形,正方形间有怎样的联系?
平行四边形
四边形
矩形
菱形
对角线相等
对角线垂直
从对角线考虑:
对角线
互相平分
问题3:
菱形,矩形,正方形间有怎样的联系?
平行四边形
四边形
矩形
菱形
正方形
对角线相等
对角线垂直
对角线垂直
从对角线考虑:
对角线
互相平分
问题3:
菱形,矩形,正方形间有怎样的联系?
平行四边形
四边形
矩形
菱形
正方形
对角线相等
对角线垂直
对角线相等
对角线垂直
从对角线考虑:
对角线
互相平分
问题3:
菱形,矩形,正方形间有怎样的联系?
平行四边形
四边形
矩形
菱形
正方形
对角线相等
对角线垂直
对角线相等
对角线垂直
对角线垂直且相等
从对角线考虑:
对角线
互相平分
学以致用
解决问题
例
判断下列说法是否正确?为什么?
学以致用
解决问题
(1)如果一个菱形的两条对角线相等,那么它一定是正方形.
例
判断下列说法是否正确?为什么?
学以致用
解决问题
(1)如果一个菱形的两条对角线相等,那么它一定是正方形.
例
判断下列说法是否正确?为什么?
矩形特性
菱形+两条对角线相等
分析:
学以致用
解决问题
(1)如果一个菱形的两条对角线相等,那么它一定是正方形.
例
判断下列说法是否正确?为什么?
答:正确.
矩形特性
菱形+两条对角线相等
正方形
分析:
学以致用
解决问题
(2)如果一个矩形的两条对角线互相垂直,那么它一定是
正方形.
例
判断下列说法是否正确?为什么?
学以致用
解决问题
(2)如果一个矩形的两条对角线互相垂直,那么它一定是
正方形.
例
判断下列说法是否正确?为什么?
菱形特性
矩形+两条对角线互相垂直
分析:
学以致用
解决问题
(2)如果一个矩形的两条对角线互相垂直,那么它一定是
正方形.
例
判断下列说法是否正确?为什么?
菱形特性
矩形+两条对角线互相垂直
分析:
正方形
答:正确.
学以致用
解决问题
(3)对角线互相垂直平分且相等的四边形,一定是正方形.
例
判断下列说法是否正确?为什么?
学以致用
解决问题
(3)对角线互相垂直平分且相等的四边形,一定是正方形.
例
判断下列说法是否正确?为什么?
对角线互相垂直
+
菱形特性
矩形特性
对角线互相平分
+
平行四边形
对角线相等
分析:
学以致用
解决问题
(3)对角线互相垂直平分且相等的四边形,一定是正方形.
例
判断下列说法是否正确?为什么?
对角线互相垂直
+
菱形特性
矩形特性
对角线互相平分
+
平行四边形
对角线相等
分析:
正方形
答:正确.
学以致用
解决问题
(4)四条边相等,且有一个角是直角的四边形是正方形.
例
判断下列说法是否正确?为什么?
学以致用
解决问题
(4)四条边相等,且有一个角是直角的四边形是正方形.
例
判断下列说法是否正确?为什么?
四条边相等
菱形
+
有一个角是直角
分析:
学以致用
解决问题
(4)四条边相等,且有一个角是直角的四边形是正方形.
例
判断下列说法是否正确?为什么?
四条边相等
菱形
+
有一个角是直角
分析:
答:正确.
正方形
例
如图,在△
ABC中,∠ACB=90°,CF为∠ACB的平分线,
FD⊥AC于点D,FE⊥BC于点E,试说明四边形CDFE是正方形.
例
如图,在△
ABC中,∠ACB=90°,CF为∠ACB的平分线,
FD⊥AC于点D,FE⊥BC于点E,试说明四边形CDFE是正方形.
分析:
题目中FD⊥AC,FE⊥BC,∠ACB=90°
易得出四边形CDFE是矩形.
例
如图,在△
ABC中,∠ACB=90°,CF为∠ACB的平分线,
FD⊥AC于点D,FE⊥BC于点E,试说明四边形CDFE是正方形.
分析:
题目中FD⊥AC,FE⊥BC,∠ACB=90°
易得出四边形CDFE是矩形.
由此我们思考:矩形加什么条件
可以得到正方形?
例
如图,在△
ABC中,∠ACB=90°,CF为∠ACB的平分线,
FD⊥AC于点D,FE⊥BC于点E,试说明四边形CDFE是正方形.
分析:
既是矩形又是菱形
正方形
有一组邻边相等或对角线互相垂直
例
如图,在△
ABC中,∠ACB=90°,CF为∠ACB的平分线,
FD⊥AC于点D,FE⊥BC于点E,试说明四边形CDFE是正方形.
分析:
由CF为∠ACB的平分线,利用角平分
线定理易知FD=FE.
例
如图,在△
ABC中,∠ACB=90°,CF为∠ACB的平分线,
FD⊥AC于点D,FE⊥BC于点E,试说明四边形CDFE是正方形.
分析:
由CF为∠ACB的平分线,利用角平分
线定理易知FD=FE.
矩形
+
正方形
有一组邻边相等
例
如图,在△
ABC中,∠ACB=90°,CF为∠ACB的平分线,
FD⊥AC于点D,FE⊥BC于点E,试说明四边形CDFE是正方形.
解:∵EF⊥BC,FD⊥AC,
∠ACB=90°,
∴∠FEC=∠FDC=∠ACB=90°.
∴
四边形CDFE为矩形.
解:又∵CF平分∠ACB,
∴FD=FE
.
∴矩形CDFE为正方形.
例
如图,在△
ABC中,∠ACB=90°,CF为∠ACB的平分线,
FD⊥AC于点D,FE⊥BC于点E,试说明四边形CDFE是正方形.
例
如图,在平面直角坐标系中,顺次连接点A(-2,0),
B(0,-2),C(2,0),D(0,2)所得到的四边形
ABCD是怎样的四边形?并说明理由.
例
如图,在平面直角坐标系中,顺次连接点A(-2,0),
B(0,-2),C(2,0),D(0,2)所得到的四边形
ABCD是怎样的四边形?并说明理由.
分析:
由
A(-2,0),B(0,-2),
C(2,0),
D(0,2),
易得出A,B,C,D到原点的距离
都是2.
例
如图,在平面直角坐标系中,顺次连接点A(-2,0),
B(0,-2),C(2,0),D(0,2)所得到的四边形
ABCD是怎样的四边形?并说明理由.
分析:
得到对角线相等,且互相
平分.
例
如图,在平面直角坐标系中,顺次连接点A(-2,0),
B(0,-2),C(2,0),D(0,2)所得到的四边形
ABCD是怎样的四边形?并说明理由.
分析:
由平面直角坐标系,易知AC⊥BD.
例
如图,在平面直角坐标系中,顺次连接点A(-2,0),
B(0,-2),C(2,0),D(0,2)所得到的四边形
ABCD是怎样的四边形?并说明理由.
分析:
对角线相等
且互相平分
+
对角线
互相垂直
正方形
例
如图,在平面直角坐标系中,顺次连接点A(-2,0),
B(0,-2),C(2,0),D(0,2)所得到的四边形
ABCD是怎样的四边形?并说明理由.
解:∵A(-2,0),B(0,-2),
C(2,0),
D(0,2),
∴OA=OB=OC=OD=2.
∴AC=BD=4.
例
如图,在平面直角坐标系中,顺次连接点A(-2,0),
B(0,-2),C(2,0),D(0,2)所得到的四边形
ABCD是怎样的四边形?并说明理由.
解:又∵AC⊥BD,
∴四边形ABCD是正方形.
回顾判定
小结提升
1.本节课你学习了什么知识?
回顾判定
小结提升
1.本节课你学习了什么知识?
正方形的判定方法:关键在于判定它既是菱形又是矩形.
回顾判定
小结提升
1.本节课你学习了什么知识?
(2)在菱形的基础上,判定有一个角是直角或对角线
相等.
(1)定义法:有一组邻边相等并且有一个角是直角的平
行四边形是正方形.
正方形的判定方法:关键在于判定它既是菱形又是矩形.
回顾判定
小结提升
1.本节课你学习了什么知识?
(4)在四边形的基础上,判定对角线相等并且互相垂
直平分.
(3)在矩形的基础上,判定有一组邻边相等或对角线
互相垂直.
正方形的判定方法:
2.本节课你感受到了哪些数学方法?
2.本节课你感受到了哪些数学方法?
(1)从一般到特殊:
平行四边形
正方形.
边特殊化
角特殊化
2.本节课你感受到了哪些数学方法?
(1)从一般到特殊:
平行四边形
正方形.
边特殊化
(2)用运动的观点看问题:
改变菱形的角,当有一个角是直角时,菱形成为正方形.
改变矩形的边,当矩形的邻边相等时,矩形成为正方形.
角特殊化
3.本节课你感悟到的解题思路是什么?
3.本节课你感悟到的解题思路是什么?
矩形
菱形
正方形
有一组邻边相等
或对角线相等
或对角线互相垂直
有一个角是直角
四边形
对角线相等
且互相垂直平分
课堂练习
巩固判定
已知如图,点D是△ABC的BC边上的中点,DE⊥AB,
DF⊥AC,垂足分别是E和F,且BE=CF,∠A=90°,试判
断四边形AFDE的形状.
希望同学们可以像完美正方形一样取得完美的学习效
果,加油!
完美正方形:一个大正方形由若干个大小各不相同的
小正方形构成,那么大正方形叫做完美正方形.
例:如图,菱形ABCD的对角线AC和BD相交于点O,请你添加一个条件,使菱形ABCD成为正方形,并说明理由.
初二年级
数学
正方形的判定
我们已经学习了平行四边形,矩形和菱形,它们是如何判定的?
复习回顾
引出课题
平行四边形的判定
两组对边分别平行的四边形
两组对边分别相等的四边形
对角线互相平分的四边形
一组对边平行且相等的四边形
矩形的判定
菱形的判定
有一个角是直角的
平行四边形
对角线相等的
平行四边形
有三个角是直角的四边形
矩形的判定
菱形的判定
有一个角是直角的
平行四边形
一组邻边相等的
平行四边形
对角线相等的
平行四边形
有三个角是直角的四边形
对角线互相垂直的
平行四边形
四边相等的四边形
平行四边形
菱形
一组邻边相等
平行四边形
矩形
有一个角直角
问题:如果平行四边形的边和角一起特殊化,
能得到什么呢?
平行四边形
正方形
一个角是直角
一组邻边相等
正方形的定义:
有一组邻边相等并且有一个角是直角
的平行四边形叫做正方形.
平行四边形
正方形
一个角是直角
一组邻边相等
判定一个四边形是正方形的关键在于
判定它既是菱形又是矩形.
探究猜想
归纳判定
问题:明明在商场中想买一块正方形纱巾,但不知是否
是正方形的,只见售货员阿姨拉起纱巾的一组对
角,能完全重合,重合后变成三角形,在此基础
上,将另两个顶点再对折,也能完全重合.
阿姨
认为这样能够证明是正方形,把纱巾给了明明,
你认为明明手上的纱巾一定是正方形吗?
“对折两次,能够完全重合”实际上告诉了我们什么?
分析:
“对折两次,能够完全重合”实际上告诉了我们什么?
分析:
四边相等,对角线互相垂直平分,即纱巾的
两条对角线所在的直线是对称轴.由此我们只
能保证纱巾是菱形.
如果要判断纱巾是正方形,还需要在菱形的基础上判定
它是矩形.因此还需要添加什么条件?
思考:
如果要判断纱巾是正方形,还需要在菱形的基础上判定
它是矩形.因此还需要添加什么条件?
思考:
有一个角是直角.实际上改变菱形的角,
当有一个角是直角时,菱形就变成了正方形.
当有一个角是直角
从对角线来考虑,在菱形的基础上,对角线满足什么条件可以得到正方形?
当对角线相等
?
猜想:对角线相等的菱形是正方形.
分析:平行四边形+对角线相等
矩形
有一个角是直角
已知:四边形ABCD是菱形,AC=BD.
求证:四边形ABCD是正方形.
猜想:对角线相等的菱形是正方形
证明:∵四边形ABCD是菱形,
∴四边形ABCD是平行四边形,
AB=AD.
已知:四边形ABCD是菱形,AC=BD.
求证:四边形ABCD是正方形.
猜想:对角线相等的菱形是正方形
已知:四边形ABCD是菱形,AC=BD.
求证:四边形ABCD是正方形.
证明:∵AC=BD,
∴四边形ABCD是矩形.
∴∠DAB=90°.
∴四边形ABCD是正方形.
(1)在菱形的基础上:
判定有一个角是直角或对角线相等.
符号语言:
∵四边形ABCD是菱形,∠BAD=90°(或AC=BD),
∴四边形ABCD是正方形.
判定有一个角是直角或对角线相等.
(1)在菱形的基础上:
问题:
如果在矩形的基础上判断一个四边形是正方形,
需要添加什么条件?
要使一个矩形成为正方形,还需添加一组邻边相等.
实际上改变矩形的边,当矩形的邻边相等时,矩形
就成为正方形.
当有一组邻边相等
问题:
如果在矩形的基础上判断一个四边形正方形,
需要添加什么条件?
从对角线来考虑,在矩形的基础上,对角线满足什么条件可以得到正方形?
当对角线互相垂直
?
猜想:对角线互相垂直的矩形是正方形.
分析:平行四边形+对角线互相垂直
菱形
有一组邻边相等
已知:四边形ABCD是矩形,AC⊥BD.
求证:四边形ABCD是正方形.
猜想:对角线互相垂直的矩形是正方形.
已知:四边形ABCD是矩形,AC⊥BD.
求证:四边形ABCD是正方形.
证明:∵四边形ABCD是矩形,
∴四边形ABCD是平行四边形,
∠DAB=90°.
证明:∵AC⊥BD,
∴四边形ABCD是菱形.
∴AB=AD.
∴四边形ABCD是正方形.
猜想:对角线互相垂直的矩形是正方形.
已知:四边形ABCD是矩形,AC⊥BD.
求证:四边形ABCD是正方形.
判定有一组邻边相等或者对角线互相
垂直.
(2)在矩形的基础上:
符号语言:
∵四边形ABCD是矩形,BA=BC(或AC⊥BD),
∴四边形ABCD是正方形.
(2)在矩形的基础上:
判定有一组邻边相等或者对角线互相
垂直.
在四边形的基础上,添加什么条件可以得到正方形?
当对角线相等
且互相垂直平分
?
猜想:对角线相等且互相垂直平分的四边形是正方形.
分析:对角线互相平分
平行四边形
已知:在四边形ABCD中,AC=BD,AC⊥BD,
OA=OC,OB=OD.
求证:四边形ABCD是正方形.
平行四边形+对角线垂直
菱形
有一组邻边相等
有一个角是直角
平行四边形+对角线相等
矩形
证明:∵OA=OC,OB=OD,
∴四边形ABCD是平行四边形.
∵AC=BD,
∴四边形ABCD是矩形.
∴∠DAB=90°.
猜想:对角线相等且互相垂直平分的四边形是正方形.
已知:在四边形ABCD中,AC=BD,AC⊥BD,
OA=OC,OB=OD.
求证:四边形ABCD是正方形.
证明:∵AC⊥BD,
∴四边形ABCD是菱形.
∴AB=AD.
∴四边形ABCD是正方形.
猜想:对角线相等且互相垂直平分的四边形是正方形.
已知:在四边形ABCD中,AC=BD,AC⊥BD,
OA=OC,OB=OD.
求证:四边形ABCD是正方形.
判定对角线相等,并且互相垂直平分.
(3)在四边形的基础上:
符号语言:
∵AC=BD,AC⊥BD,AO=CO,BO=DO,
∴四边形ABCD是正方形.
判定对角线相等,并且互相垂直平分.
(3)在四边形的基础上:
问题3:
菱形,矩形,正方形间有怎样的联系?
平行四边形
四边形
从边和角考虑:
两组对边
分别平行
问题3:
菱形,矩形,正方形间有怎样的联系?
平行四边形
四边形
一个角是直角
从边和角考虑:
两组对边
分别平行
矩形
问题3:
菱形,矩形,正方形间有怎样的联系?
平行四边形
四边形
矩形
菱形
一个角是直角
一组邻边相等
从边和角考虑:
两组对边
分别平行
问题3:
菱形,矩形,正方形间有怎样的联系?
平行四边形
四边形
矩形
菱形
正方形
一个角是直角
一组邻边相等
一组邻边相等
从边和角考虑:
两组对边
分别平行
问题3:
菱形,矩形,正方形间有怎样的联系?
平行四边形
四边形
矩形
菱形
正方形
一个角是直角
一组邻边相等
一个角是直角
一组邻边相等
从边和角考虑:
两组对边
分别平行
问题3:
菱形,矩形,正方形间有怎样的联系?
平行四边形
四边形
矩形
菱形
正方形
一个角是直角
一组邻边相等
一个角是直角
一组邻边相等
一个角是直角
一组邻边相等
从边和角考虑:
两组对边
分别平行
问题3:
菱形,矩形,正方形间有怎样的联系?
平行四边形
四边形
从对角线考虑:
对角线
互相平分
问题3:
菱形,矩形,正方形间有怎样的联系?
平行四边形
四边形
矩形
对角线相等
从对角线考虑:
对角线
互相平分
问题3:
菱形,矩形,正方形间有怎样的联系?
平行四边形
四边形
矩形
菱形
对角线相等
对角线垂直
从对角线考虑:
对角线
互相平分
问题3:
菱形,矩形,正方形间有怎样的联系?
平行四边形
四边形
矩形
菱形
正方形
对角线相等
对角线垂直
对角线垂直
从对角线考虑:
对角线
互相平分
问题3:
菱形,矩形,正方形间有怎样的联系?
平行四边形
四边形
矩形
菱形
正方形
对角线相等
对角线垂直
对角线相等
对角线垂直
从对角线考虑:
对角线
互相平分
问题3:
菱形,矩形,正方形间有怎样的联系?
平行四边形
四边形
矩形
菱形
正方形
对角线相等
对角线垂直
对角线相等
对角线垂直
对角线垂直且相等
从对角线考虑:
对角线
互相平分
学以致用
解决问题
例
判断下列说法是否正确?为什么?
学以致用
解决问题
(1)如果一个菱形的两条对角线相等,那么它一定是正方形.
例
判断下列说法是否正确?为什么?
学以致用
解决问题
(1)如果一个菱形的两条对角线相等,那么它一定是正方形.
例
判断下列说法是否正确?为什么?
矩形特性
菱形+两条对角线相等
分析:
学以致用
解决问题
(1)如果一个菱形的两条对角线相等,那么它一定是正方形.
例
判断下列说法是否正确?为什么?
答:正确.
矩形特性
菱形+两条对角线相等
正方形
分析:
学以致用
解决问题
(2)如果一个矩形的两条对角线互相垂直,那么它一定是
正方形.
例
判断下列说法是否正确?为什么?
学以致用
解决问题
(2)如果一个矩形的两条对角线互相垂直,那么它一定是
正方形.
例
判断下列说法是否正确?为什么?
菱形特性
矩形+两条对角线互相垂直
分析:
学以致用
解决问题
(2)如果一个矩形的两条对角线互相垂直,那么它一定是
正方形.
例
判断下列说法是否正确?为什么?
菱形特性
矩形+两条对角线互相垂直
分析:
正方形
答:正确.
学以致用
解决问题
(3)对角线互相垂直平分且相等的四边形,一定是正方形.
例
判断下列说法是否正确?为什么?
学以致用
解决问题
(3)对角线互相垂直平分且相等的四边形,一定是正方形.
例
判断下列说法是否正确?为什么?
对角线互相垂直
+
菱形特性
矩形特性
对角线互相平分
+
平行四边形
对角线相等
分析:
学以致用
解决问题
(3)对角线互相垂直平分且相等的四边形,一定是正方形.
例
判断下列说法是否正确?为什么?
对角线互相垂直
+
菱形特性
矩形特性
对角线互相平分
+
平行四边形
对角线相等
分析:
正方形
答:正确.
学以致用
解决问题
(4)四条边相等,且有一个角是直角的四边形是正方形.
例
判断下列说法是否正确?为什么?
学以致用
解决问题
(4)四条边相等,且有一个角是直角的四边形是正方形.
例
判断下列说法是否正确?为什么?
四条边相等
菱形
+
有一个角是直角
分析:
学以致用
解决问题
(4)四条边相等,且有一个角是直角的四边形是正方形.
例
判断下列说法是否正确?为什么?
四条边相等
菱形
+
有一个角是直角
分析:
答:正确.
正方形
例
如图,在△
ABC中,∠ACB=90°,CF为∠ACB的平分线,
FD⊥AC于点D,FE⊥BC于点E,试说明四边形CDFE是正方形.
例
如图,在△
ABC中,∠ACB=90°,CF为∠ACB的平分线,
FD⊥AC于点D,FE⊥BC于点E,试说明四边形CDFE是正方形.
分析:
题目中FD⊥AC,FE⊥BC,∠ACB=90°
易得出四边形CDFE是矩形.
例
如图,在△
ABC中,∠ACB=90°,CF为∠ACB的平分线,
FD⊥AC于点D,FE⊥BC于点E,试说明四边形CDFE是正方形.
分析:
题目中FD⊥AC,FE⊥BC,∠ACB=90°
易得出四边形CDFE是矩形.
由此我们思考:矩形加什么条件
可以得到正方形?
例
如图,在△
ABC中,∠ACB=90°,CF为∠ACB的平分线,
FD⊥AC于点D,FE⊥BC于点E,试说明四边形CDFE是正方形.
分析:
既是矩形又是菱形
正方形
有一组邻边相等或对角线互相垂直
例
如图,在△
ABC中,∠ACB=90°,CF为∠ACB的平分线,
FD⊥AC于点D,FE⊥BC于点E,试说明四边形CDFE是正方形.
分析:
由CF为∠ACB的平分线,利用角平分
线定理易知FD=FE.
例
如图,在△
ABC中,∠ACB=90°,CF为∠ACB的平分线,
FD⊥AC于点D,FE⊥BC于点E,试说明四边形CDFE是正方形.
分析:
由CF为∠ACB的平分线,利用角平分
线定理易知FD=FE.
矩形
+
正方形
有一组邻边相等
例
如图,在△
ABC中,∠ACB=90°,CF为∠ACB的平分线,
FD⊥AC于点D,FE⊥BC于点E,试说明四边形CDFE是正方形.
解:∵EF⊥BC,FD⊥AC,
∠ACB=90°,
∴∠FEC=∠FDC=∠ACB=90°.
∴
四边形CDFE为矩形.
解:又∵CF平分∠ACB,
∴FD=FE
.
∴矩形CDFE为正方形.
例
如图,在△
ABC中,∠ACB=90°,CF为∠ACB的平分线,
FD⊥AC于点D,FE⊥BC于点E,试说明四边形CDFE是正方形.
例
如图,在平面直角坐标系中,顺次连接点A(-2,0),
B(0,-2),C(2,0),D(0,2)所得到的四边形
ABCD是怎样的四边形?并说明理由.
例
如图,在平面直角坐标系中,顺次连接点A(-2,0),
B(0,-2),C(2,0),D(0,2)所得到的四边形
ABCD是怎样的四边形?并说明理由.
分析:
由
A(-2,0),B(0,-2),
C(2,0),
D(0,2),
易得出A,B,C,D到原点的距离
都是2.
例
如图,在平面直角坐标系中,顺次连接点A(-2,0),
B(0,-2),C(2,0),D(0,2)所得到的四边形
ABCD是怎样的四边形?并说明理由.
分析:
得到对角线相等,且互相
平分.
例
如图,在平面直角坐标系中,顺次连接点A(-2,0),
B(0,-2),C(2,0),D(0,2)所得到的四边形
ABCD是怎样的四边形?并说明理由.
分析:
由平面直角坐标系,易知AC⊥BD.
例
如图,在平面直角坐标系中,顺次连接点A(-2,0),
B(0,-2),C(2,0),D(0,2)所得到的四边形
ABCD是怎样的四边形?并说明理由.
分析:
对角线相等
且互相平分
+
对角线
互相垂直
正方形
例
如图,在平面直角坐标系中,顺次连接点A(-2,0),
B(0,-2),C(2,0),D(0,2)所得到的四边形
ABCD是怎样的四边形?并说明理由.
解:∵A(-2,0),B(0,-2),
C(2,0),
D(0,2),
∴OA=OB=OC=OD=2.
∴AC=BD=4.
例
如图,在平面直角坐标系中,顺次连接点A(-2,0),
B(0,-2),C(2,0),D(0,2)所得到的四边形
ABCD是怎样的四边形?并说明理由.
解:又∵AC⊥BD,
∴四边形ABCD是正方形.
回顾判定
小结提升
1.本节课你学习了什么知识?
回顾判定
小结提升
1.本节课你学习了什么知识?
正方形的判定方法:关键在于判定它既是菱形又是矩形.
回顾判定
小结提升
1.本节课你学习了什么知识?
(2)在菱形的基础上,判定有一个角是直角或对角线
相等.
(1)定义法:有一组邻边相等并且有一个角是直角的平
行四边形是正方形.
正方形的判定方法:关键在于判定它既是菱形又是矩形.
回顾判定
小结提升
1.本节课你学习了什么知识?
(4)在四边形的基础上,判定对角线相等并且互相垂
直平分.
(3)在矩形的基础上,判定有一组邻边相等或对角线
互相垂直.
正方形的判定方法:
2.本节课你感受到了哪些数学方法?
2.本节课你感受到了哪些数学方法?
(1)从一般到特殊:
平行四边形
正方形.
边特殊化
角特殊化
2.本节课你感受到了哪些数学方法?
(1)从一般到特殊:
平行四边形
正方形.
边特殊化
(2)用运动的观点看问题:
改变菱形的角,当有一个角是直角时,菱形成为正方形.
改变矩形的边,当矩形的邻边相等时,矩形成为正方形.
角特殊化
3.本节课你感悟到的解题思路是什么?
3.本节课你感悟到的解题思路是什么?
矩形
菱形
正方形
有一组邻边相等
或对角线相等
或对角线互相垂直
有一个角是直角
四边形
对角线相等
且互相垂直平分
课堂练习
巩固判定
已知如图,点D是△ABC的BC边上的中点,DE⊥AB,
DF⊥AC,垂足分别是E和F,且BE=CF,∠A=90°,试判
断四边形AFDE的形状.
希望同学们可以像完美正方形一样取得完美的学习效
果,加油!
完美正方形:一个大正方形由若干个大小各不相同的
小正方形构成,那么大正方形叫做完美正方形.
例:如图,菱形ABCD的对角线AC和BD相交于点O,请你添加一个条件,使菱形ABCD成为正方形,并说明理由.
同课章节目录
