人教版八年级下册数学 18.2.1矩形的判定 课件(55张ppt)
文档属性
| 名称 | 人教版八年级下册数学 18.2.1矩形的判定 课件(55张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 7.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-26 00:00:00 | ||
图片预览







文档简介
(共55张PPT)
初二年级
数学
矩形的判定
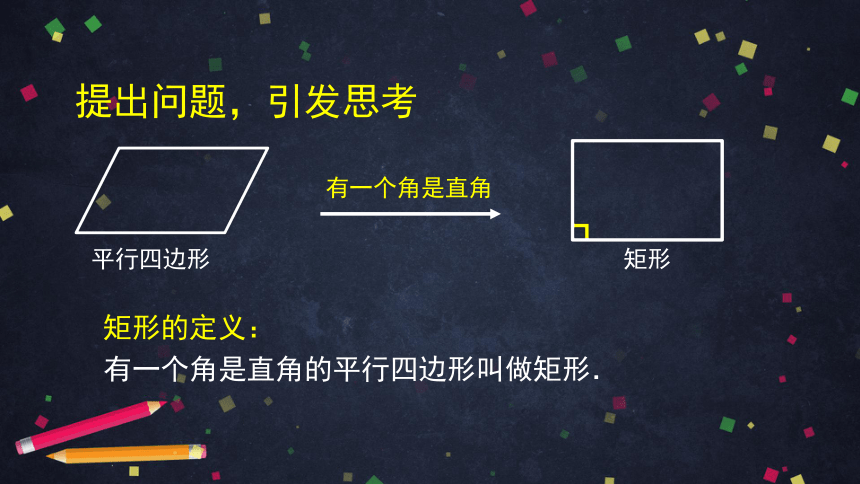
矩形的定义:
有一个角是直角的平行四边形叫做矩形.
提出问题,引发思考
平行四边形
矩形
有一个角是直角
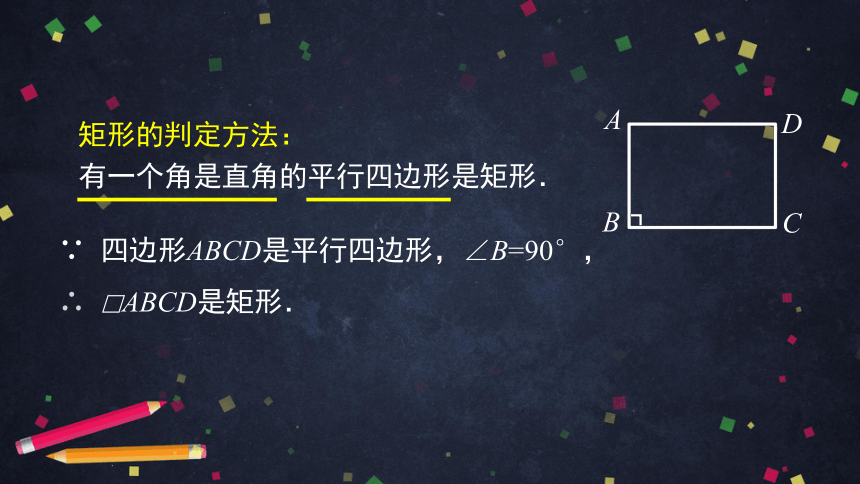
矩形的判定方法:
有一个角是直角的平行四边形是矩形.
∵
四边形ABCD是平行四边形,∠B=90°,
∴
□ABCD是矩形.
D
C
B
A
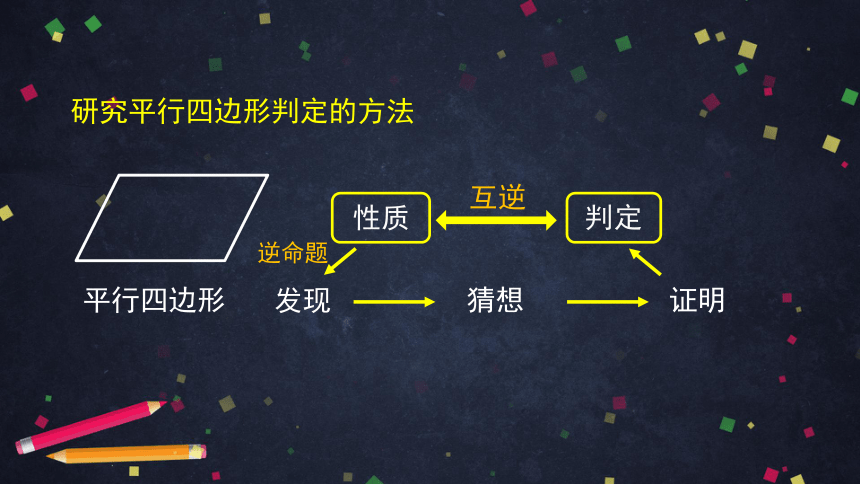
平行四边形
发现
猜想
证明
互逆
性质
判定
研究平行四边形判定的方法
逆命题
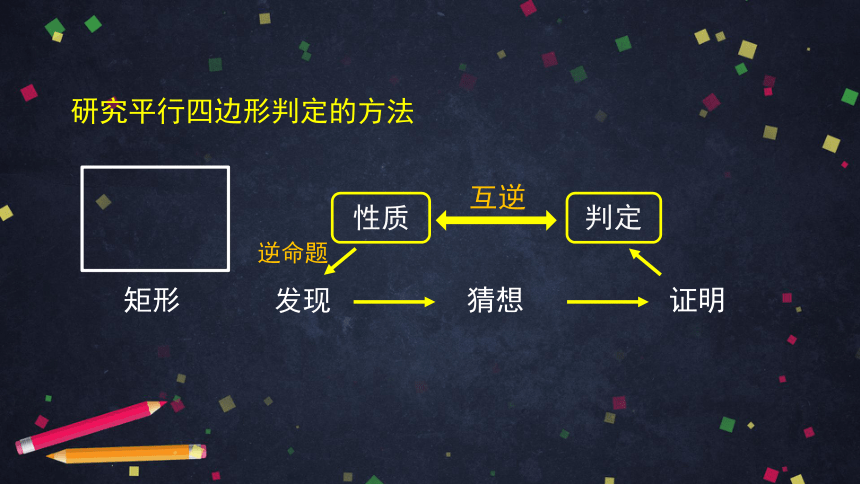
发现
猜想
证明
互逆
性质
判定
研究平行四边形判定的方法
逆命题
矩形
矩形
与平行四边形相同的性质
特殊的性质
边
角
对角线
矩形的性质
对边平行且相等
四个角都是直角
对角线互相平分
对角线相等
对角相等、邻角互补
对角线相等的平行四边形是矩形.
矩形的对角线相等.
对角线的角度
结论
题设
猜想:对角线相等的平行四边形是矩形.
已知:如图,四边形ABCD是平行四边形,
AC=BD.
求证:□ABCD是矩形.
A
B
C
D
依据矩形的定义
证明□ABCD是矩形
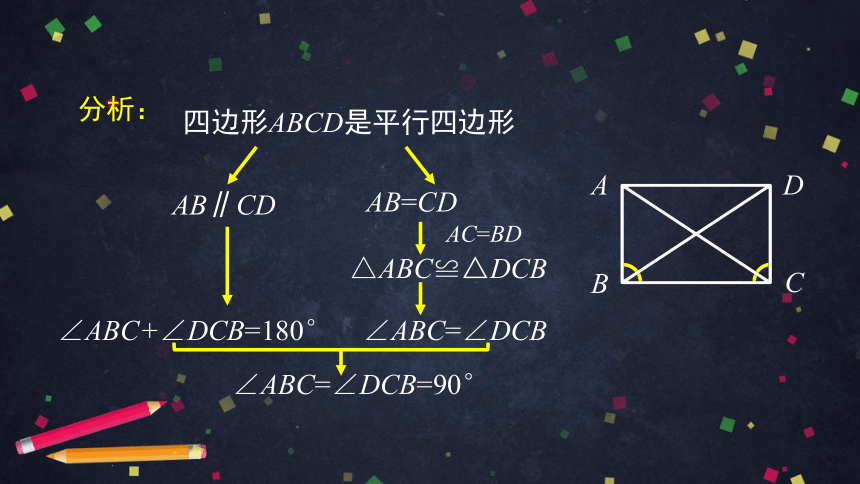
分析:
∠ABC=90°
A
B
C
D
∠ABC=∠DCB
四边形ABCD是平行四边形
AB=CD
△ABC≌△DCB
AB∥CD
∠ABC+∠DCB=180°
∠ABC=∠DCB=90°
AC=BD
分析:
A
B
C
D
∵
四边形ABCD是平行四边形,
∴
AB∥CD,AB=CD.
∴
∠ABC+∠DCB=180°.
∵
AC=BD,BC=CB,
∴
△ABC≌△DCB.
∴
∠ABC=∠DCB.
A
B
C
D
证明:
∴
∠ABC=90°.
∴
□ABCD是矩形.
A
B
C
D
矩形的判定定理:
对角线相等的平行四边形是矩形.
∵ 四边形ABCD是平行四边形,
AC=BD,
∴
□ABCD是矩形.
A
B
C
D
矩形的判定方法:
有一个角是直角的平行四边形是矩形.
对角线相等的平行四边形是矩形.
矩形
与平行四边形相同的性质
特殊的性质
边
角
对角线
矩形的性质
对边平行且相等
四个角都是直角
对角线互相平分
对角线相等
对角相等、邻角互补
矩形的四个角都是直角.
结论
题设
四个角都是直角的四边形是矩形.
角的角度
猜想:有三个角是直角的四边形是矩形.
四边形内角
和是360°
D
C
B
A
∠A=∠B=∠C=90°
∠A=∠B=∠C=∠D=90°
角的角度
猜想:有三个角是直角的四边形是矩形.
已知:如图,四边形ABCD中,
∠A=∠B=∠C=90°.
求证:四边形ABCD是矩形.
D
C
B
A
依据矩形的定义
分析:
四边形ABCD是平行四边形
证明四边形ABCD是矩形
∠A=∠B=∠C=90°
D
C
B
A
AD∥BC,AB∥DC
四边形ABCD是平行四边形
∠A+∠B=180°∠B+∠C=180°
分析:
∠D=90°
∠A=∠C,∠B=∠D
D
C
B
A
∠A=∠B=∠C=90°
∵
∠A=∠B=∠C=90°,
∴
∠A+∠B=180°,∠B+∠C=180°.
∴
AD∥BC,AB∥DC.
∴
四边形ABCD是平行四边形.
∵
∠B=90°,
∴ 平行四边形ABCD是矩形.
D
C
B
A
证明:
矩形的判定定理:
有三个角是直角的四边形是矩形.
∵ 四边形ABCD中,
∠A=∠B=∠C=90°,
∴
四边形ABCD是矩形.
D
C
B
A
矩形的判定方法:
有一个角是直角的平行四边形是矩形.
有三个角是直角的四边形是矩形.
D
C
B
A
AD∥BC,AB∥DC
四边形ABCD是平行四边形
∠A+∠B=180°∠B+∠C=180°
∠A=∠B=∠C=90°
有三个角是直角的四边形是矩形.
有两个角是直角的四边形
矩形的判定方法:
对角线相等的平行四边形是矩形.
四边形是矩形.
对角线相等且互相平分的
对角线相等的四边形
矩形的判定方法:
有一个角是直角的平行四边形是矩形.
对角线相等的平行四边形是矩形.
有三个角是直角的四边形是矩形.
对角线相等且互相平分的四边形是矩形.
四边形
平行四边形
矩形
有一个角是直角
对角线相等
有三个角是直角
对角线相等且互相平分
发现
猜想
证明
性质
判定
研究矩形判定的方法
矩形
平行四边形
类比
工人师傅在做门窗或矩形零件时,不仅要测量两组对边的长度是否相等,常常还要测量它们的两条对角线是否相等,以确保图形是矩形.
你知道其中的道理吗?
运用定理,解决问题
对角线相等的平行四边形是矩形.
平行四边形
例
如图,在△ABC中,AB=AC,D是BC中点.四边形ABDE是平行四边形,DE交AC于点F,连接CE.
求证:四边形ADCE是矩形.
A
D
C
E
F
B
例
如图,在△ABC中,AB=AC,D是BC中点.四边形ABDE是平行四边形,DE交AC于点F,连接CE.
求证:四边形ADCE是矩形.
分析:
AB=AC,D是BC中点
AD⊥DC
A
D
C
E
F
B
∠ADC=90°
A
D
C
E
F
B
分析:
□ABDE
D是BC中点
AE∥BD
BD=CD
AE=BD
AE∥CD
AE=CD
□ADCE
□ADCE是矩形
∠ADC=90°
A
D
C
E
F
B
∵
AB=AC,D是BC中点,
∴
AD⊥DC,BD=CD.
∵
四边形ABDE是平行四边形,
∴
AE∥BD,AE=BD.
∴
AE∥DC,AE=DC.
∴
四边形ADCE是平行四边形.
又
∠ADC=90°,
∴
□ADCE是矩形.
证明
:
例
如图,在△ABC中,AB=AC,D是BC中点.四边形ABDE是平行四边形,DE交AC于点F,连接CE.
求证:四边形ADCE是矩形.
分析:
AB=DE
A
D
C
E
F
B
□ABDE
AC=DE
A
D
C
E
F
B
∵
四边形ABDE是平行四边形,
∴
AE∥BD,AE=BD,AB=DE.
∵
AB=AC,
∴
AC=DE.
∵
D是BC中点,
∴
BD=CD.
∴
AE=CD.
证明
:
A
D
C
E
F
B
又
AE∥DC,
∴
四边形ADCE是平行四边形.
∴
□ADCE是矩形.
例题小结
判定
矩形
角
对角线
有一个角是直角的平行四边形是矩形
对角线相等的平行四边形是矩形
有三个角是直角的四边形是矩形
例
如图,在□ABCD中,对角线AC,BD相交于点O,且OA=OD,∠OAD=50°.求∠OAB的度数.
A
B
C
D
O
A
B
C
D
O
分析:
□ABCD
□ABCD是矩形
分析:
∠OAB=∠DAB-∠OAD=40°
□ABCD是矩形
∠DAB=90°
A
B
C
D
O
50°
∵
四边形ABCD是平行四边形,
∴
.
又
OA=OD,
∴
AC=BD.
∴
四边形ABCD是矩形.
∴
∠DAB=90°.
又
∠OAD=50°,
∴
∠OAB=∠DAB-∠OAD=40°.
A
B
C
D
O
解
:
例题小结
矩形
四边形
运用矩形性质
平行四边形
边
角
对角线
练习
如图,□ABCD的对角线AC,BD相交于点O,
△OAB是等边三角形,且AB=4.求□ABCD的面积.
A
B
C
D
O
A
B
C
D
O
分析:
□ABCD是矩形
AC=BD
□ABCD
OA=OB=AB
等边三角形△OAB
求矩形ABCD的面积
求BC的长
分析:
A
B
C
D
O
∠ABC=90°
AB=4
A
B
C
D
O
BC
∠ABC=90°
△ABC是直角三角形
四边形ABCD是矩形
分析:
A
B
C
D
O
∵
四边形ABCD是平行四边形,
∴
.
又
△OAB是等边三角形,AB=4,
∴
OA=OB=AB=4.
∴
AC=BD=8.
∴
四边形ABCD是矩形.
∴
∠ABC=90°.
解:
A
B
C
D
O
在Rt△ABC中,
,
∴
.
∴
.
平行四边形
类比
矩形
定义
性质
判定
归纳总结,提升认识
互
逆
角
对角线
四边形
对角线相等且互相平分的四边形是矩形
对角线相等的平行四边形是矩形
有一个角是直角的平行四边形
有三个角是直角的四边形是矩形
一般
特殊
课后作业
1.八年级(3)班同学要在广场上布置一个矩形的花坛,
计划用红花摆成两条对角线.如果一条对角线用了38盆
红花,还需要从花房运来多少盆红花?为什么?如果一
条对角线用了49盆呢?
课后作业
2.如图,四边形ABCD是平行四边形,对角线AC,BD相交
于点O,且∠1=∠2.它是一个矩形吗?为什么?
A
B
C
D
O
1
2
课后作业
3.一个木匠要制作矩形的踏板,他在一个对边平行的长木
板上分别沿与长边垂直的方向锯了两次,就能得到矩形
踏板.为什么?
同学们再见!
初二年级
数学
矩形的判定
矩形的定义:
有一个角是直角的平行四边形叫做矩形.
提出问题,引发思考
平行四边形
矩形
有一个角是直角
矩形的判定方法:
有一个角是直角的平行四边形是矩形.
∵
四边形ABCD是平行四边形,∠B=90°,
∴
□ABCD是矩形.
D
C
B
A
平行四边形
发现
猜想
证明
互逆
性质
判定
研究平行四边形判定的方法
逆命题
发现
猜想
证明
互逆
性质
判定
研究平行四边形判定的方法
逆命题
矩形
矩形
与平行四边形相同的性质
特殊的性质
边
角
对角线
矩形的性质
对边平行且相等
四个角都是直角
对角线互相平分
对角线相等
对角相等、邻角互补
对角线相等的平行四边形是矩形.
矩形的对角线相等.
对角线的角度
结论
题设
猜想:对角线相等的平行四边形是矩形.
已知:如图,四边形ABCD是平行四边形,
AC=BD.
求证:□ABCD是矩形.
A
B
C
D
依据矩形的定义
证明□ABCD是矩形
分析:
∠ABC=90°
A
B
C
D
∠ABC=∠DCB
四边形ABCD是平行四边形
AB=CD
△ABC≌△DCB
AB∥CD
∠ABC+∠DCB=180°
∠ABC=∠DCB=90°
AC=BD
分析:
A
B
C
D
∵
四边形ABCD是平行四边形,
∴
AB∥CD,AB=CD.
∴
∠ABC+∠DCB=180°.
∵
AC=BD,BC=CB,
∴
△ABC≌△DCB.
∴
∠ABC=∠DCB.
A
B
C
D
证明:
∴
∠ABC=90°.
∴
□ABCD是矩形.
A
B
C
D
矩形的判定定理:
对角线相等的平行四边形是矩形.
∵ 四边形ABCD是平行四边形,
AC=BD,
∴
□ABCD是矩形.
A
B
C
D
矩形的判定方法:
有一个角是直角的平行四边形是矩形.
对角线相等的平行四边形是矩形.
矩形
与平行四边形相同的性质
特殊的性质
边
角
对角线
矩形的性质
对边平行且相等
四个角都是直角
对角线互相平分
对角线相等
对角相等、邻角互补
矩形的四个角都是直角.
结论
题设
四个角都是直角的四边形是矩形.
角的角度
猜想:有三个角是直角的四边形是矩形.
四边形内角
和是360°
D
C
B
A
∠A=∠B=∠C=90°
∠A=∠B=∠C=∠D=90°
角的角度
猜想:有三个角是直角的四边形是矩形.
已知:如图,四边形ABCD中,
∠A=∠B=∠C=90°.
求证:四边形ABCD是矩形.
D
C
B
A
依据矩形的定义
分析:
四边形ABCD是平行四边形
证明四边形ABCD是矩形
∠A=∠B=∠C=90°
D
C
B
A
AD∥BC,AB∥DC
四边形ABCD是平行四边形
∠A+∠B=180°∠B+∠C=180°
分析:
∠D=90°
∠A=∠C,∠B=∠D
D
C
B
A
∠A=∠B=∠C=90°
∵
∠A=∠B=∠C=90°,
∴
∠A+∠B=180°,∠B+∠C=180°.
∴
AD∥BC,AB∥DC.
∴
四边形ABCD是平行四边形.
∵
∠B=90°,
∴ 平行四边形ABCD是矩形.
D
C
B
A
证明:
矩形的判定定理:
有三个角是直角的四边形是矩形.
∵ 四边形ABCD中,
∠A=∠B=∠C=90°,
∴
四边形ABCD是矩形.
D
C
B
A
矩形的判定方法:
有一个角是直角的平行四边形是矩形.
有三个角是直角的四边形是矩形.
D
C
B
A
AD∥BC,AB∥DC
四边形ABCD是平行四边形
∠A+∠B=180°∠B+∠C=180°
∠A=∠B=∠C=90°
有三个角是直角的四边形是矩形.
有两个角是直角的四边形
矩形的判定方法:
对角线相等的平行四边形是矩形.
四边形是矩形.
对角线相等且互相平分的
对角线相等的四边形
矩形的判定方法:
有一个角是直角的平行四边形是矩形.
对角线相等的平行四边形是矩形.
有三个角是直角的四边形是矩形.
对角线相等且互相平分的四边形是矩形.
四边形
平行四边形
矩形
有一个角是直角
对角线相等
有三个角是直角
对角线相等且互相平分
发现
猜想
证明
性质
判定
研究矩形判定的方法
矩形
平行四边形
类比
工人师傅在做门窗或矩形零件时,不仅要测量两组对边的长度是否相等,常常还要测量它们的两条对角线是否相等,以确保图形是矩形.
你知道其中的道理吗?
运用定理,解决问题
对角线相等的平行四边形是矩形.
平行四边形
例
如图,在△ABC中,AB=AC,D是BC中点.四边形ABDE是平行四边形,DE交AC于点F,连接CE.
求证:四边形ADCE是矩形.
A
D
C
E
F
B
例
如图,在△ABC中,AB=AC,D是BC中点.四边形ABDE是平行四边形,DE交AC于点F,连接CE.
求证:四边形ADCE是矩形.
分析:
AB=AC,D是BC中点
AD⊥DC
A
D
C
E
F
B
∠ADC=90°
A
D
C
E
F
B
分析:
□ABDE
D是BC中点
AE∥BD
BD=CD
AE=BD
AE∥CD
AE=CD
□ADCE
□ADCE是矩形
∠ADC=90°
A
D
C
E
F
B
∵
AB=AC,D是BC中点,
∴
AD⊥DC,BD=CD.
∵
四边形ABDE是平行四边形,
∴
AE∥BD,AE=BD.
∴
AE∥DC,AE=DC.
∴
四边形ADCE是平行四边形.
又
∠ADC=90°,
∴
□ADCE是矩形.
证明
:
例
如图,在△ABC中,AB=AC,D是BC中点.四边形ABDE是平行四边形,DE交AC于点F,连接CE.
求证:四边形ADCE是矩形.
分析:
AB=DE
A
D
C
E
F
B
□ABDE
AC=DE
A
D
C
E
F
B
∵
四边形ABDE是平行四边形,
∴
AE∥BD,AE=BD,AB=DE.
∵
AB=AC,
∴
AC=DE.
∵
D是BC中点,
∴
BD=CD.
∴
AE=CD.
证明
:
A
D
C
E
F
B
又
AE∥DC,
∴
四边形ADCE是平行四边形.
∴
□ADCE是矩形.
例题小结
判定
矩形
角
对角线
有一个角是直角的平行四边形是矩形
对角线相等的平行四边形是矩形
有三个角是直角的四边形是矩形
例
如图,在□ABCD中,对角线AC,BD相交于点O,且OA=OD,∠OAD=50°.求∠OAB的度数.
A
B
C
D
O
A
B
C
D
O
分析:
□ABCD
□ABCD是矩形
分析:
∠OAB=∠DAB-∠OAD=40°
□ABCD是矩形
∠DAB=90°
A
B
C
D
O
50°
∵
四边形ABCD是平行四边形,
∴
.
又
OA=OD,
∴
AC=BD.
∴
四边形ABCD是矩形.
∴
∠DAB=90°.
又
∠OAD=50°,
∴
∠OAB=∠DAB-∠OAD=40°.
A
B
C
D
O
解
:
例题小结
矩形
四边形
运用矩形性质
平行四边形
边
角
对角线
练习
如图,□ABCD的对角线AC,BD相交于点O,
△OAB是等边三角形,且AB=4.求□ABCD的面积.
A
B
C
D
O
A
B
C
D
O
分析:
□ABCD是矩形
AC=BD
□ABCD
OA=OB=AB
等边三角形△OAB
求矩形ABCD的面积
求BC的长
分析:
A
B
C
D
O
∠ABC=90°
AB=4
A
B
C
D
O
BC
∠ABC=90°
△ABC是直角三角形
四边形ABCD是矩形
分析:
A
B
C
D
O
∵
四边形ABCD是平行四边形,
∴
.
又
△OAB是等边三角形,AB=4,
∴
OA=OB=AB=4.
∴
AC=BD=8.
∴
四边形ABCD是矩形.
∴
∠ABC=90°.
解:
A
B
C
D
O
在Rt△ABC中,
,
∴
.
∴
.
平行四边形
类比
矩形
定义
性质
判定
归纳总结,提升认识
互
逆
角
对角线
四边形
对角线相等且互相平分的四边形是矩形
对角线相等的平行四边形是矩形
有一个角是直角的平行四边形
有三个角是直角的四边形是矩形
一般
特殊
课后作业
1.八年级(3)班同学要在广场上布置一个矩形的花坛,
计划用红花摆成两条对角线.如果一条对角线用了38盆
红花,还需要从花房运来多少盆红花?为什么?如果一
条对角线用了49盆呢?
课后作业
2.如图,四边形ABCD是平行四边形,对角线AC,BD相交
于点O,且∠1=∠2.它是一个矩形吗?为什么?
A
B
C
D
O
1
2
课后作业
3.一个木匠要制作矩形的踏板,他在一个对边平行的长木
板上分别沿与长边垂直的方向锯了两次,就能得到矩形
踏板.为什么?
同学们再见!
