人教版八年级下册数学 18.2.2菱形的性质 课件(64张ppt)
文档属性
| 名称 | 人教版八年级下册数学 18.2.2菱形的性质 课件(64张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 8.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-26 08:18:29 | ||
图片预览







文档简介
(共64张PPT)
初二年级
数学
菱
形
的
性
质
生活中美丽的菱形图案
菱形是特殊的平行四边形
提出问题,引发思考
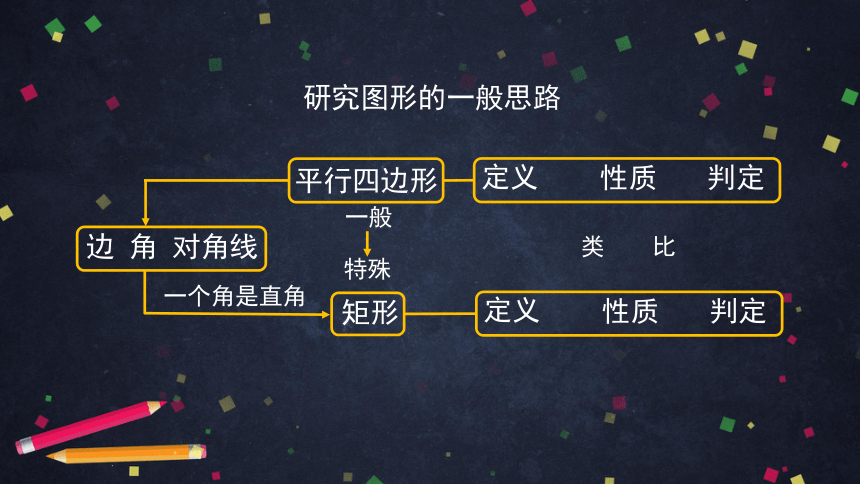
研究图形的一般思路
定义
性质
判定
平行四边形
边
角
对角线
研究图形的一般思路
类
比
一般
特殊
定义
性质
判定
矩形
一个角是直角
定义
性质
判定
平行四边形
边
角
对角线
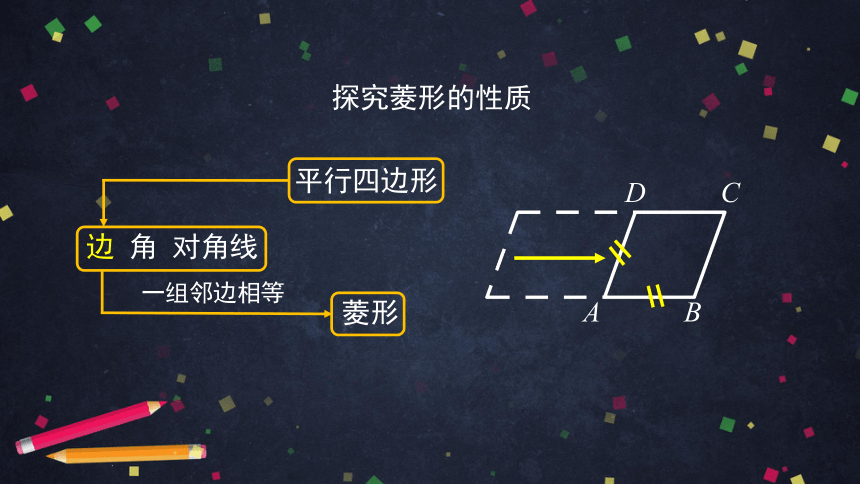
探究菱形的性质
平行四边形
A
B
C
D
平行四边形
菱形
A
B
C
D
一组邻边相等
边
角
对角线
探究菱形的性质
菱形的定义:
有一组邻边相等的平行四边形叫做菱形.
∵
四边形ABCD是平行四边形,
∵
四边形ABCD是菱形,
∴
四边形ABCD是平行四边形,
AB=BC.
A
B
C
D
菱形ABCD
AB=BC,
∴
四边形ABCD是菱形.
对角线互相平分
对角
线
菱
形
特殊的性质
对角相等(邻角互补)
角
对边平行且相等
边
与平行四边形相同的性质
邻边相等
定义
探究性质,深化认识
平行四边形
菱形
一组邻边相等
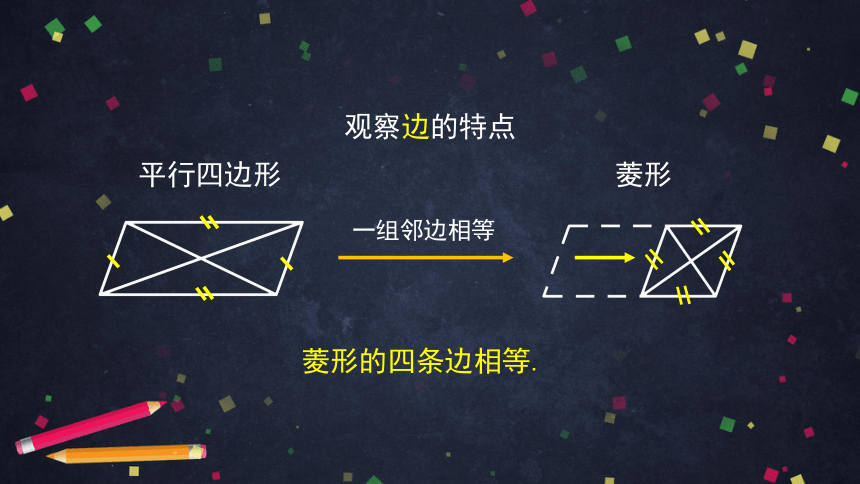
观察边的特点
菱形的四条边相等.
四条边都相等
对角线互相平分
对角
线
菱
形
特殊的性质
对角相等(邻角互补)
角
对边平行且相等
边
与平行四边形相同的性质
邻边相等
定义
平行四边形
菱形
一组邻边相等
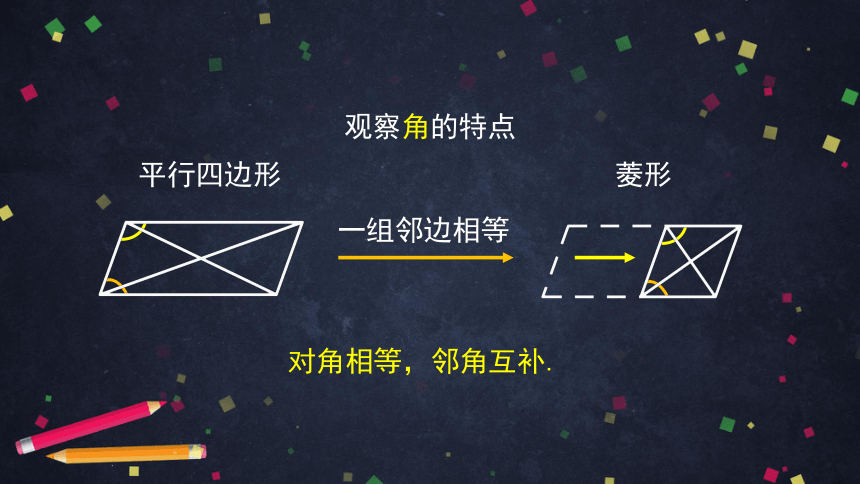
观察角的特点
对角相等,邻角互补.
平行四边形
菱形
一组邻边相等
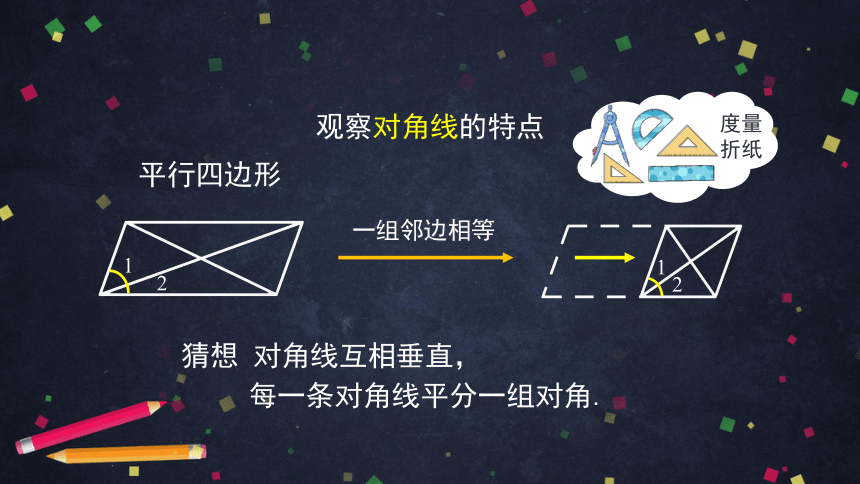
观察对角线的特点
猜想
对角线互相垂直,
每一条对角线平分一组对角.
度量
折纸
1
2
2
1
四条边都相等
对角线互相垂直
对角线平分对角
对角线互相平分
对角
线
菱
形
特殊的性质
对角相等(邻角互补)
角
对边平行且相等
边
与平行四边形相同的性质
邻边相等
定义
有关菱形特殊性质的猜想
猜想1
菱形的四条边都相等.
猜想2
菱形的两条对角线互相垂直,
并且每一条对角线平分一组对角.
猜想1
菱形的四条边都相等.
已知:如图,四边形ABCD是菱形.
求证:AB=BC=CD=AD.
平行四边形
AB=CD
AD=BC
AB=AD
邻边相等
+
分析:
A
B
C
D
已知:如图,四边形ABCD是菱形.
求证:AB=BC=CD=AD.
证明:∵
四边形ABCD是菱形,
∴
AB=AD,AB=CD,AD=BC.
∴
AB=BC=CD=AD.
猜想1
菱形的四条边都相等.
A
B
C
D
∵
四边形ABCD是菱形,
∴
AB=BC=CD=AD.
A
B
C
D
菱形的四条边都相等.
菱形的特殊性质:
猜想2
菱形的两条对角线互相垂直,并且
每一条对角线平分一组对角.
已知:如图,四边形ABCD是菱形,对角线AC,BD相交于点O.
求证:AC⊥BD,
DB平分∠ADC,
BD平分∠ABC,
AC平分∠DAB,
CA平分∠DCB.
要证AC⊥BD,DB平分∠ADC.
OA=OC
分析:
(△ADC是等腰三角形)
AD=DC
邻边相等
+
平行四边形
四边形ABCD是菱形
A
B
C
D
O
已知:如图,四边形ABCD是菱形,对角线AC,BD相交于点O.
求证:AC⊥BD,
DB平分∠ADC,
BD平分∠ABC,
AC平分∠DAB,
CA平分∠DCB.
A
B
C
D
O
A
B
C
D
O
A
B
C
D
O
证明:∵
四边形ABCD是菱形,
∴
AD=DC,且OA=OC.
∴
AC⊥BD,DB平分∠ADC.
同理
BD平分∠ABC,
AC平分∠DAB,
CA平分∠DCB.
菱形的两条对角线互相垂直,并且每一条对角线
平分一组对角.
∵
四边形ABCD是菱形,
∴
AC⊥BD,
DB平分∠ADC,BD平分∠ABC,
AC平分∠DAB,
CA平分∠DCB.
A
B
C
D
O
菱形的特殊性质:
A
B
C
D
O
A
B
C
D
O
比较一般的平行四边形和菱形被两条对角线分得
的8个角之间有怎样的数量关系?
1
2
3
4
5
6
7
8
1
2
3
4
5
6
7
8
∠1=∠5
∠2=∠6
∠3=∠7
∠4=∠8
∠1=∠5
∠2=∠6
∠3=∠7
∠4=∠8
=
=
菱形不同于一般平行四边形的特殊性质:
菱形的四条边都相等;
菱形的两条对角线互相垂直,并且每一条对角线平分
一组对角.
菱形所有的性质:
菱形的四条边都相等,对边平行;
菱形的两条对角线互相垂直平分,
并且每一条对角线平分一组对角.
菱形的对角相等,邻角互补;
A
B
C
D
O
菱形的四条边都相等,对边平行;
菱形的两条对角线互相垂直平分,
并且每一条对角线平分一组对角.
菱形的对角相等,邻角互补;
菱形所有的性质:
A
B
C
D
A
B
C
D
菱形的两条对角线互相垂直平分,
并且每一条对角线平分一组对角.
菱形的对角相等,邻角互补;
菱形的四条边都相等,对边平行;
菱形所有的性质:
轴对称图形
菱形的四条边都相等,对边平行;
菱形的两条对角线互相垂直平分,
并且每一条对角线平分一组对角.
菱形的对角相等,邻角互补;
菱形所有的性质:
A
B
C
D
O
全等三角形
等腰三角形
直角三角形
线段的垂直平分线
例
如图,菱形花坛ABCD的边长
为20
m,∠ABC=60°,沿着菱形的对角
线修建了两条小路AC和BD.求两条小路
的长(结果保留小数点后两位)和花坛
的面积(结果保留小数点后一位).
运用性质,解决问题
B
C
O
含
角的直角三角形
A
B
C
D
O
分析:
菱形花坛ABCD的边长为20
m,∠ABC=60°.
A
B
C
等边三角形
AC=2CO=20
BD=2BO=20
CO=10
BO=10
例
如图,菱形花坛ABCD的边长
为20
m,∠ABC=60°,沿着菱形的对角
线修建了两条小路AC和BD.求两条小路
的长(结果保留小数点后两位)和花坛
的面积(结果保留小数点后一位).
底
高
分析:方法1
分析:方法2
菱形的面积等于它的两条对角线长的积的一半.
菱形面积的求法:
A
B
C
D
O
解:∵
花坛ABCD的形状是菱形,
∴
AC⊥BD,∠CBO=
∠ABC=30°.
在Rt
△BOC中,CO=
BC=10,
∴
AC=2CO=20(m)
,BD=2BO=20
(m).
∴
S
菱形
.
.
例题小结
等边三角形
等腰三角形
一个内角为
的菱形
直角三角形
等腰三角形
直角三角形
菱形
例题小结
菱形的面积等于它的两条对角线长的积的一半.
S
菱形
例
如图,E,F分别是菱形ABCD的边AB,AD的
中点,且AB=5,AC=6.
(1)△OEF是什么三角形?证明你的结论.
(2)求线段EF的长.
A
B
C
D
F
E
O
例
如图,E,F分别是菱形ABCD的边AB,AD的
中点,且AB=5,AC=6.
(1)△OEF是什么三角形?证明你的结论.
△OEF是等腰三角形
证明OE=OF
A
B
C
D
F
E
O
分析:
证明OE=OF
A
B
C
D
F
E
O
分析:
证明OE=OF
证明△BOE
≌
△DOF
方法1
A
B
C
D
F
E
O
A
B
C
D
F
E
O
证明△AOE
≌
△AOF
A
B
C
D
F
E
O
A
B
C
D
F
E
O
分析:
证明OE=OF
证明∠OEF=∠OFE
方法2
分析:
证明OE=OF
方法3
A
B
C
D
F
E
O
分析:
证明OE=OF
OE
=
AB
OF
=
AD
AB
=
AD
方法3
A
B
C
D
F
E
O
分析:
证明OE=OF
点O
线段AC的中点
线段BD的中点
方法4
A
B
C
D
F
E
O
分析:
证明OE=OF
OE
=
BC
方法4
A
B
C
D
F
E
O
分析:
证明OE=OF
OE
=
BC
OF
=
CD
BC
=
CD
方法4
A
B
C
D
F
E
O
分析:
证明OE=OF
全等三角形
等腰三角形
直角三角形
斜边中线
三角形
的中位线
(1)
(2)
(3)
(4)
(1)证明:∵
四边形ABCD是菱形,
∴
AB=AD,
AC⊥BD.
在Rt△AOB中,OE是AB边上的中线,
∴
OE=
AB.
同理
OF=
AD.
∴
OE=OF.
∴
△OEF是等腰三角形.
A
B
C
D
F
E
O
例
如图,E,F分别是菱形ABCD的边AB,AD的
中点,且AB=5,AC=6.
(2)求线段EF的长.
分析:
A
B
C
D
F
E
O
例
如图,E,F分别是菱形ABCD的边AB,AD的
中点,且AB=5,AC=6.
(2)求线段EF的长.
分析:
EF
=
BD
OB
=
BD
求线段OB的长度
5
3
4
A
B
C
D
F
E
O
(2)解:∵
E,F是AB,AD的中点,
∴
EF是△ABD的中位线.
∴
.
∵
四边形ABCD是菱形,
AC=6,
∴
AC⊥BD,
.
∴
EF=OB.
EF
=
BD
OB
=
BD
OA
=
AC=3,
A
B
C
D
F
E
O
(2)解:
在Rt△AOB中,
AB=5,OA=3,
∴
EF=OB=4.
.
A
B
C
D
F
E
O
例题小结
中点
对角线
互相平分
直角三角形
对角线
互相垂直
三角形
中位线
等腰
三角形
线段的
垂直平分线
勾股
定理
特殊的
直角三角形
斜边中线
菱形所有的性质:
菱形的四条边都相等,对边平行;
菱形的两条对角线互相垂直平分,并且每一条对角线平分一组对角.
菱形的对角相等,邻角互补;
A
B
C
D
O
课堂小结
平行四边形
矩形
菱形
一个角是直角
一组邻边相等
平行四边形
矩
形
特殊四边形
菱
形
直角三角形
等腰三角形
全等三角形
转
化
三角形
1.
四边形ABCD是菱形,对角线AC,BD相交于点O,
且
AB=13,AO=12.
求AC
和BD的长.
布置作业
2.
已知菱形的两条对角线的长分别是6和8,求菱形
的周长和面积.
3.
如图,四边形ABCD是菱形,∠ACD=30°,BD=6.求:
(1)∠BAD,∠ABC的度数;
(2)AB,AC的长.
4.
如图,四边形ABCD是菱形,AC=8,DB=6,
DH⊥AB于点H.求DH的长.
A
B
C
D
O
H
5.
如图,四边形ABCD是菱形,C,D两点的坐标
分别是(c,0),(0,d),点A,B在坐标轴上.
求A,B两点的坐标.
同
学
们
,再
见!
初二年级
数学
菱
形
的
性
质
生活中美丽的菱形图案
菱形是特殊的平行四边形
提出问题,引发思考
研究图形的一般思路
定义
性质
判定
平行四边形
边
角
对角线
研究图形的一般思路
类
比
一般
特殊
定义
性质
判定
矩形
一个角是直角
定义
性质
判定
平行四边形
边
角
对角线
探究菱形的性质
平行四边形
A
B
C
D
平行四边形
菱形
A
B
C
D
一组邻边相等
边
角
对角线
探究菱形的性质
菱形的定义:
有一组邻边相等的平行四边形叫做菱形.
∵
四边形ABCD是平行四边形,
∵
四边形ABCD是菱形,
∴
四边形ABCD是平行四边形,
AB=BC.
A
B
C
D
菱形ABCD
AB=BC,
∴
四边形ABCD是菱形.
对角线互相平分
对角
线
菱
形
特殊的性质
对角相等(邻角互补)
角
对边平行且相等
边
与平行四边形相同的性质
邻边相等
定义
探究性质,深化认识
平行四边形
菱形
一组邻边相等
观察边的特点
菱形的四条边相等.
四条边都相等
对角线互相平分
对角
线
菱
形
特殊的性质
对角相等(邻角互补)
角
对边平行且相等
边
与平行四边形相同的性质
邻边相等
定义
平行四边形
菱形
一组邻边相等
观察角的特点
对角相等,邻角互补.
平行四边形
菱形
一组邻边相等
观察对角线的特点
猜想
对角线互相垂直,
每一条对角线平分一组对角.
度量
折纸
1
2
2
1
四条边都相等
对角线互相垂直
对角线平分对角
对角线互相平分
对角
线
菱
形
特殊的性质
对角相等(邻角互补)
角
对边平行且相等
边
与平行四边形相同的性质
邻边相等
定义
有关菱形特殊性质的猜想
猜想1
菱形的四条边都相等.
猜想2
菱形的两条对角线互相垂直,
并且每一条对角线平分一组对角.
猜想1
菱形的四条边都相等.
已知:如图,四边形ABCD是菱形.
求证:AB=BC=CD=AD.
平行四边形
AB=CD
AD=BC
AB=AD
邻边相等
+
分析:
A
B
C
D
已知:如图,四边形ABCD是菱形.
求证:AB=BC=CD=AD.
证明:∵
四边形ABCD是菱形,
∴
AB=AD,AB=CD,AD=BC.
∴
AB=BC=CD=AD.
猜想1
菱形的四条边都相等.
A
B
C
D
∵
四边形ABCD是菱形,
∴
AB=BC=CD=AD.
A
B
C
D
菱形的四条边都相等.
菱形的特殊性质:
猜想2
菱形的两条对角线互相垂直,并且
每一条对角线平分一组对角.
已知:如图,四边形ABCD是菱形,对角线AC,BD相交于点O.
求证:AC⊥BD,
DB平分∠ADC,
BD平分∠ABC,
AC平分∠DAB,
CA平分∠DCB.
要证AC⊥BD,DB平分∠ADC.
OA=OC
分析:
(△ADC是等腰三角形)
AD=DC
邻边相等
+
平行四边形
四边形ABCD是菱形
A
B
C
D
O
已知:如图,四边形ABCD是菱形,对角线AC,BD相交于点O.
求证:AC⊥BD,
DB平分∠ADC,
BD平分∠ABC,
AC平分∠DAB,
CA平分∠DCB.
A
B
C
D
O
A
B
C
D
O
A
B
C
D
O
证明:∵
四边形ABCD是菱形,
∴
AD=DC,且OA=OC.
∴
AC⊥BD,DB平分∠ADC.
同理
BD平分∠ABC,
AC平分∠DAB,
CA平分∠DCB.
菱形的两条对角线互相垂直,并且每一条对角线
平分一组对角.
∵
四边形ABCD是菱形,
∴
AC⊥BD,
DB平分∠ADC,BD平分∠ABC,
AC平分∠DAB,
CA平分∠DCB.
A
B
C
D
O
菱形的特殊性质:
A
B
C
D
O
A
B
C
D
O
比较一般的平行四边形和菱形被两条对角线分得
的8个角之间有怎样的数量关系?
1
2
3
4
5
6
7
8
1
2
3
4
5
6
7
8
∠1=∠5
∠2=∠6
∠3=∠7
∠4=∠8
∠1=∠5
∠2=∠6
∠3=∠7
∠4=∠8
=
=
菱形不同于一般平行四边形的特殊性质:
菱形的四条边都相等;
菱形的两条对角线互相垂直,并且每一条对角线平分
一组对角.
菱形所有的性质:
菱形的四条边都相等,对边平行;
菱形的两条对角线互相垂直平分,
并且每一条对角线平分一组对角.
菱形的对角相等,邻角互补;
A
B
C
D
O
菱形的四条边都相等,对边平行;
菱形的两条对角线互相垂直平分,
并且每一条对角线平分一组对角.
菱形的对角相等,邻角互补;
菱形所有的性质:
A
B
C
D
A
B
C
D
菱形的两条对角线互相垂直平分,
并且每一条对角线平分一组对角.
菱形的对角相等,邻角互补;
菱形的四条边都相等,对边平行;
菱形所有的性质:
轴对称图形
菱形的四条边都相等,对边平行;
菱形的两条对角线互相垂直平分,
并且每一条对角线平分一组对角.
菱形的对角相等,邻角互补;
菱形所有的性质:
A
B
C
D
O
全等三角形
等腰三角形
直角三角形
线段的垂直平分线
例
如图,菱形花坛ABCD的边长
为20
m,∠ABC=60°,沿着菱形的对角
线修建了两条小路AC和BD.求两条小路
的长(结果保留小数点后两位)和花坛
的面积(结果保留小数点后一位).
运用性质,解决问题
B
C
O
含
角的直角三角形
A
B
C
D
O
分析:
菱形花坛ABCD的边长为20
m,∠ABC=60°.
A
B
C
等边三角形
AC=2CO=20
BD=2BO=20
CO=10
BO=10
例
如图,菱形花坛ABCD的边长
为20
m,∠ABC=60°,沿着菱形的对角
线修建了两条小路AC和BD.求两条小路
的长(结果保留小数点后两位)和花坛
的面积(结果保留小数点后一位).
底
高
分析:方法1
分析:方法2
菱形的面积等于它的两条对角线长的积的一半.
菱形面积的求法:
A
B
C
D
O
解:∵
花坛ABCD的形状是菱形,
∴
AC⊥BD,∠CBO=
∠ABC=30°.
在Rt
△BOC中,CO=
BC=10,
∴
AC=2CO=20(m)
,BD=2BO=20
(m).
∴
S
菱形
.
.
例题小结
等边三角形
等腰三角形
一个内角为
的菱形
直角三角形
等腰三角形
直角三角形
菱形
例题小结
菱形的面积等于它的两条对角线长的积的一半.
S
菱形
例
如图,E,F分别是菱形ABCD的边AB,AD的
中点,且AB=5,AC=6.
(1)△OEF是什么三角形?证明你的结论.
(2)求线段EF的长.
A
B
C
D
F
E
O
例
如图,E,F分别是菱形ABCD的边AB,AD的
中点,且AB=5,AC=6.
(1)△OEF是什么三角形?证明你的结论.
△OEF是等腰三角形
证明OE=OF
A
B
C
D
F
E
O
分析:
证明OE=OF
A
B
C
D
F
E
O
分析:
证明OE=OF
证明△BOE
≌
△DOF
方法1
A
B
C
D
F
E
O
A
B
C
D
F
E
O
证明△AOE
≌
△AOF
A
B
C
D
F
E
O
A
B
C
D
F
E
O
分析:
证明OE=OF
证明∠OEF=∠OFE
方法2
分析:
证明OE=OF
方法3
A
B
C
D
F
E
O
分析:
证明OE=OF
OE
=
AB
OF
=
AD
AB
=
AD
方法3
A
B
C
D
F
E
O
分析:
证明OE=OF
点O
线段AC的中点
线段BD的中点
方法4
A
B
C
D
F
E
O
分析:
证明OE=OF
OE
=
BC
方法4
A
B
C
D
F
E
O
分析:
证明OE=OF
OE
=
BC
OF
=
CD
BC
=
CD
方法4
A
B
C
D
F
E
O
分析:
证明OE=OF
全等三角形
等腰三角形
直角三角形
斜边中线
三角形
的中位线
(1)
(2)
(3)
(4)
(1)证明:∵
四边形ABCD是菱形,
∴
AB=AD,
AC⊥BD.
在Rt△AOB中,OE是AB边上的中线,
∴
OE=
AB.
同理
OF=
AD.
∴
OE=OF.
∴
△OEF是等腰三角形.
A
B
C
D
F
E
O
例
如图,E,F分别是菱形ABCD的边AB,AD的
中点,且AB=5,AC=6.
(2)求线段EF的长.
分析:
A
B
C
D
F
E
O
例
如图,E,F分别是菱形ABCD的边AB,AD的
中点,且AB=5,AC=6.
(2)求线段EF的长.
分析:
EF
=
BD
OB
=
BD
求线段OB的长度
5
3
4
A
B
C
D
F
E
O
(2)解:∵
E,F是AB,AD的中点,
∴
EF是△ABD的中位线.
∴
.
∵
四边形ABCD是菱形,
AC=6,
∴
AC⊥BD,
.
∴
EF=OB.
EF
=
BD
OB
=
BD
OA
=
AC=3,
A
B
C
D
F
E
O
(2)解:
在Rt△AOB中,
AB=5,OA=3,
∴
EF=OB=4.
.
A
B
C
D
F
E
O
例题小结
中点
对角线
互相平分
直角三角形
对角线
互相垂直
三角形
中位线
等腰
三角形
线段的
垂直平分线
勾股
定理
特殊的
直角三角形
斜边中线
菱形所有的性质:
菱形的四条边都相等,对边平行;
菱形的两条对角线互相垂直平分,并且每一条对角线平分一组对角.
菱形的对角相等,邻角互补;
A
B
C
D
O
课堂小结
平行四边形
矩形
菱形
一个角是直角
一组邻边相等
平行四边形
矩
形
特殊四边形
菱
形
直角三角形
等腰三角形
全等三角形
转
化
三角形
1.
四边形ABCD是菱形,对角线AC,BD相交于点O,
且
AB=13,AO=12.
求AC
和BD的长.
布置作业
2.
已知菱形的两条对角线的长分别是6和8,求菱形
的周长和面积.
3.
如图,四边形ABCD是菱形,∠ACD=30°,BD=6.求:
(1)∠BAD,∠ABC的度数;
(2)AB,AC的长.
4.
如图,四边形ABCD是菱形,AC=8,DB=6,
DH⊥AB于点H.求DH的长.
A
B
C
D
O
H
5.
如图,四边形ABCD是菱形,C,D两点的坐标
分别是(c,0),(0,d),点A,B在坐标轴上.
求A,B两点的坐标.
同
学
们
,再
见!
