北师大版八年级上册数学4.4一次函数的应用课件(18张)
文档属性
| 名称 | 北师大版八年级上册数学4.4一次函数的应用课件(18张) |

|
|
| 格式 | zip | ||
| 文件大小 | 194.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-27 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
一次函数的应用
1.某商场购进一种单价为40元的篮球,如果以单价50元出售,那么每月可售出500个,根据销售经验,售价每提高1元,销售量相应减少10个;假设销售单价提高
x元,那么销售每个篮球所获得的利润是
元;这种篮球每月的销售量是
y,试用含x的代数式表示出y。
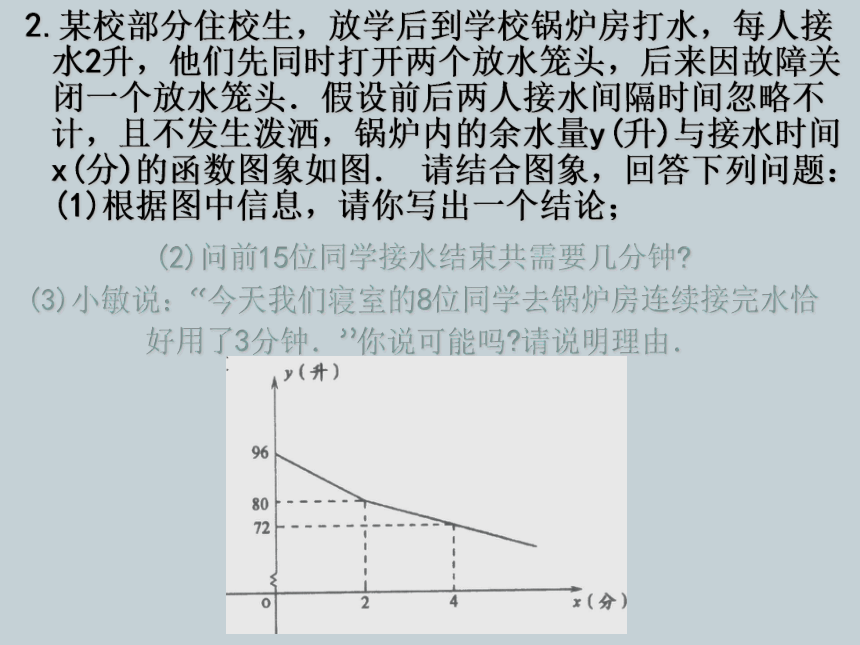
(2)问前15位同学接水结束共需要几分钟?
(3)小敏说:“今天我们寝室的8位同学去锅炉房连续接完水恰好用了3分钟.”你说可能吗?请说明理由.
2.某校部分住校生,放学后到学校锅炉房打水,每人接水2升,他们先同时打开两个放水笼头,后来因故障关闭一个放水笼头.假设前后两人接水间隔时间忽略不计,且不发生泼洒,锅炉内的余水量y(升)与接水时间x(分)的函数图象如图.
请结合图象,回答下列问题:(1)根据图中信息,请你写出一个结论;
3.A市和B市分别有某种库存机器12台和6台,现决定支援C村10台,D村8台。已知从A调运一台机器到C村和D村的运费分别是400元和800元,从B市调运一台机器到C村和D村的运费分别是300元和500元.
(1)设B市调往C村机器x台,求总运费W关于x的函数表达式
(2)若要求总运费不超过9000元,共有几种调运方案
(3)求出总运费最低的调运方案,最低运费是多少元?
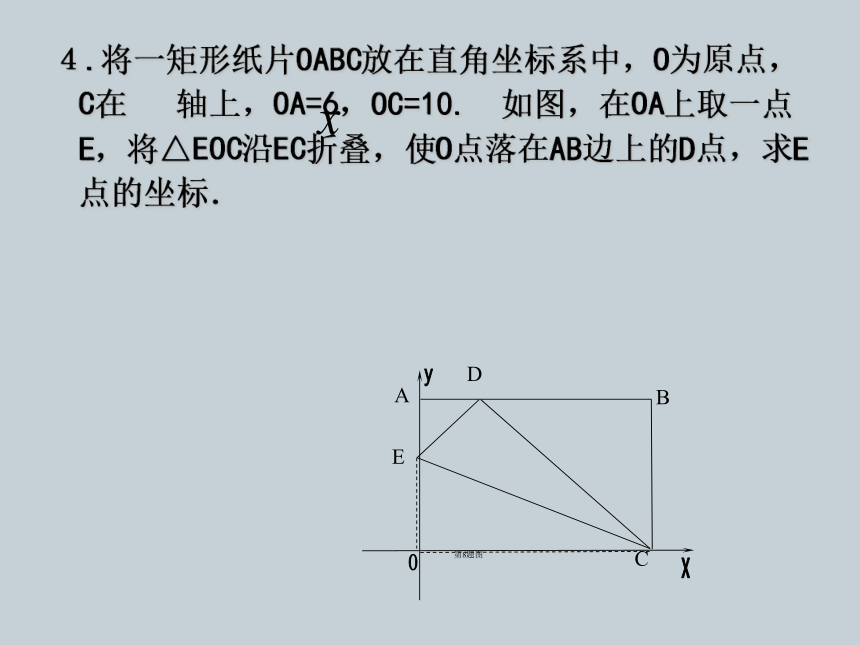
4.将一矩形纸片OABC放在直角坐标系中,O为原点,C在
轴上,OA=6,OC=10.
如图,在OA上取一点E,将△EOC沿EC折叠,使O点落在AB边上的D点,求E点的坐标.
2、加油机接到命令,立即给另一架正在飞行的运输机加油。加油过程中,设运输机的余油量为Q1吨,加油机的余油量为Q2,加油时间为t分钟,Q1
、Q2与t的函数关系如图
所示,结合图象回
答下列问题:
(1)、加油机的油箱中装了多少吨油?将这些油全部加给运输机需多少分钟?
(2)求加油过程中,运输机的余油量Q1与时间t的函数关系式:
(3)运输机加完油后,
以原速继续飞行,
需10小时到达目的地,
油料是否够用?说明
理由。
3、正方形的边长为2,顶点A(0,2),一
次函数y=x+t的图象随t的不同取值变化
时,位于l的右下方由l和正方形的边围
成的图形面积为S。
(1)
t取何值时,S=3;
(2)在平面直角坐标
系中画出S与t的函
数图象。
4.如图在矩形ABCD中,AB=10cm,BC=8cm.点P从A出发,沿A→B→C→D路线运动,到D停止;点Q从D出发,沿D→C→B→A路线运动,到A停止,若点P、点Q同时出发,点P的速度为1cm/s,点Q的速度为2cm/s,当运动到a
秒时点P、点Q同时改变速度,点P的速度变为bcm/s,点Q的速度变为d
cm/s,图
2-5-17是点
P出发x秒后△APD的面积S1(cm2)与x(s)的函数关系图象;图2-5-18是点Q出发xs后△AQD的面积S2(cm2)与x(s)的函数关系图象.
⑴
参照图2-5-17,求a、b及图中c的值;
⑵
求d的值;
⑶
设点P离开点A的路程为y1(cm),点Q到点A还需走的路程为y2(cm),请分别写出动点
P、Q改变速度后,y1、y2与出发后的运动时间x(s)的函数解析式,并求出P、Q相遇时x的值.
⑷
当点Q出发_______s时,点P、点Q在运动路线上相距的路程为25cm.
5、如图1是甲、乙两个圆柱形水槽的轴截面示意图,乙槽中有一圆柱形块放其中(圆柱形铁块的下底面完全落在水槽底面上)现将甲槽中的水匀速注入乙槽,甲、乙两个水槽中水的深度y(厘米)与注水时间x(分钟)之间的关系如图2所示。根据图象提供的信息,解答下列问题:
(1)图2中折线ABC表示
槽中的深度与注水时间之间的关系,线段DE表示
槽中的深度与注水时间之间的关系(以上两空选填“甲”、或“乙”),说出点B的纵坐标表示的实际意义
(2)注水多长时间时,甲、乙两个水槽中的水的深度相同?
(3)若乙槽底面积为36平方厘米(壁厚不计),求乙槽中铁块的体积;
(4)若乙槽中铁块的体积为112立方厘米(壁厚不计),求甲槽底面积(直接写结果)。
一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶.设行驶的时间为x(时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系.
(1)根据图中信息,求线段AB所在直线的函数解析式和甲乙两地之间的距离;
一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶.设行驶的时间为x(时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系.
(2)已知两车相遇时快车比慢车多行驶40千米,若快车从甲地到达乙地所需时间为t时,求t的值;
一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶.设行驶的时间为x(时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系.
(3)若快车到达乙地后立刻返回甲地,慢车到达甲地后停止行驶,请你在图中画出快车从乙地返回到甲地过程中y关于x的函数的大致图像.
一次函数的应用
1.某商场购进一种单价为40元的篮球,如果以单价50元出售,那么每月可售出500个,根据销售经验,售价每提高1元,销售量相应减少10个;假设销售单价提高
x元,那么销售每个篮球所获得的利润是
元;这种篮球每月的销售量是
y,试用含x的代数式表示出y。
(2)问前15位同学接水结束共需要几分钟?
(3)小敏说:“今天我们寝室的8位同学去锅炉房连续接完水恰好用了3分钟.”你说可能吗?请说明理由.
2.某校部分住校生,放学后到学校锅炉房打水,每人接水2升,他们先同时打开两个放水笼头,后来因故障关闭一个放水笼头.假设前后两人接水间隔时间忽略不计,且不发生泼洒,锅炉内的余水量y(升)与接水时间x(分)的函数图象如图.
请结合图象,回答下列问题:(1)根据图中信息,请你写出一个结论;
3.A市和B市分别有某种库存机器12台和6台,现决定支援C村10台,D村8台。已知从A调运一台机器到C村和D村的运费分别是400元和800元,从B市调运一台机器到C村和D村的运费分别是300元和500元.
(1)设B市调往C村机器x台,求总运费W关于x的函数表达式
(2)若要求总运费不超过9000元,共有几种调运方案
(3)求出总运费最低的调运方案,最低运费是多少元?
4.将一矩形纸片OABC放在直角坐标系中,O为原点,C在
轴上,OA=6,OC=10.
如图,在OA上取一点E,将△EOC沿EC折叠,使O点落在AB边上的D点,求E点的坐标.
2、加油机接到命令,立即给另一架正在飞行的运输机加油。加油过程中,设运输机的余油量为Q1吨,加油机的余油量为Q2,加油时间为t分钟,Q1
、Q2与t的函数关系如图
所示,结合图象回
答下列问题:
(1)、加油机的油箱中装了多少吨油?将这些油全部加给运输机需多少分钟?
(2)求加油过程中,运输机的余油量Q1与时间t的函数关系式:
(3)运输机加完油后,
以原速继续飞行,
需10小时到达目的地,
油料是否够用?说明
理由。
3、正方形的边长为2,顶点A(0,2),一
次函数y=x+t的图象随t的不同取值变化
时,位于l的右下方由l和正方形的边围
成的图形面积为S。
(1)
t取何值时,S=3;
(2)在平面直角坐标
系中画出S与t的函
数图象。
4.如图在矩形ABCD中,AB=10cm,BC=8cm.点P从A出发,沿A→B→C→D路线运动,到D停止;点Q从D出发,沿D→C→B→A路线运动,到A停止,若点P、点Q同时出发,点P的速度为1cm/s,点Q的速度为2cm/s,当运动到a
秒时点P、点Q同时改变速度,点P的速度变为bcm/s,点Q的速度变为d
cm/s,图
2-5-17是点
P出发x秒后△APD的面积S1(cm2)与x(s)的函数关系图象;图2-5-18是点Q出发xs后△AQD的面积S2(cm2)与x(s)的函数关系图象.
⑴
参照图2-5-17,求a、b及图中c的值;
⑵
求d的值;
⑶
设点P离开点A的路程为y1(cm),点Q到点A还需走的路程为y2(cm),请分别写出动点
P、Q改变速度后,y1、y2与出发后的运动时间x(s)的函数解析式,并求出P、Q相遇时x的值.
⑷
当点Q出发_______s时,点P、点Q在运动路线上相距的路程为25cm.
5、如图1是甲、乙两个圆柱形水槽的轴截面示意图,乙槽中有一圆柱形块放其中(圆柱形铁块的下底面完全落在水槽底面上)现将甲槽中的水匀速注入乙槽,甲、乙两个水槽中水的深度y(厘米)与注水时间x(分钟)之间的关系如图2所示。根据图象提供的信息,解答下列问题:
(1)图2中折线ABC表示
槽中的深度与注水时间之间的关系,线段DE表示
槽中的深度与注水时间之间的关系(以上两空选填“甲”、或“乙”),说出点B的纵坐标表示的实际意义
(2)注水多长时间时,甲、乙两个水槽中的水的深度相同?
(3)若乙槽底面积为36平方厘米(壁厚不计),求乙槽中铁块的体积;
(4)若乙槽中铁块的体积为112立方厘米(壁厚不计),求甲槽底面积(直接写结果)。
一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶.设行驶的时间为x(时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系.
(1)根据图中信息,求线段AB所在直线的函数解析式和甲乙两地之间的距离;
一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶.设行驶的时间为x(时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系.
(2)已知两车相遇时快车比慢车多行驶40千米,若快车从甲地到达乙地所需时间为t时,求t的值;
一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶.设行驶的时间为x(时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系.
(3)若快车到达乙地后立刻返回甲地,慢车到达甲地后停止行驶,请你在图中画出快车从乙地返回到甲地过程中y关于x的函数的大致图像.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
