人教版七年级数学下册课件: 8.1 二元一次方程组(33张ppt)
文档属性
| 名称 | 人教版七年级数学下册课件: 8.1 二元一次方程组(33张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-26 00:00:00 | ||
图片预览











文档简介
(共33张PPT)
8.1
二元一次方程组
8
二元一次方程组
课时目标
1.了解二元一次方程,二元一次方程组及其解的概念,会检验所给的一组未知数的值是否是二元一次方程、二元一次方程组的解。
2.通过实例认识二元一次方程和二元一次方程组都是反映数量关系的重要数学模型,能设两个未知数并列方程组表示实际问题中的两种相关的等量关系。
探究新知
篮球联赛中,每场比赛都要分出胜负,每队胜1场得2分,负1场得1分。某队10场比赛中得到16分,那么这个队胜负场数应分别是多少?
探究新知
解:
设胜x场,则负(10-x)场,根据题意得方程
2x+(10-x)=16
解得
x=6
10-6=4
答:这个队胜6场,只负4场.
篮球联赛中,每场比赛都要分出胜负,每队胜1场得2分,负1场得1分。某队10场比赛中得到16分,那么这个队胜负场数应分别是多少?
探究新知
积分
场数
合计
负
胜
10
2x
y
16
等量关系有哪些?
那么,能设两个未知数吗?比如设胜x场,负y场;你能根据题意列出方程吗?
探究新知
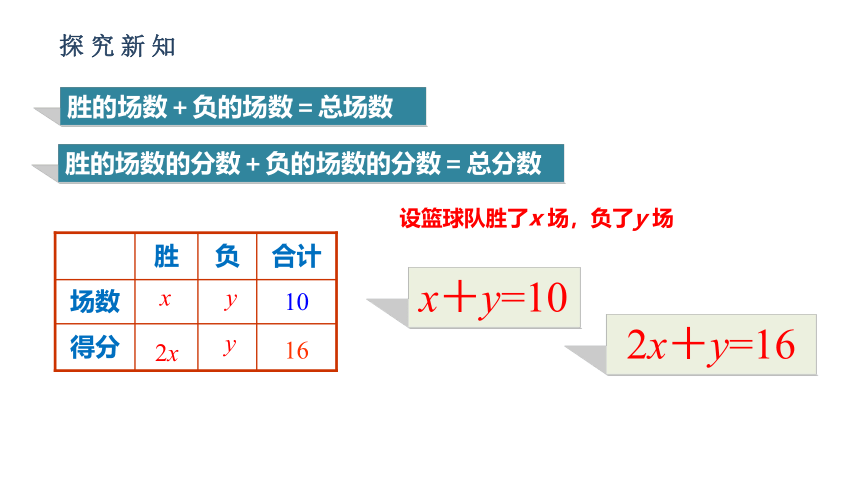
胜的场数+负的场数=总场数
胜的场数的分数+负的场数的分数=总分数
设篮球队胜了x
场,负了y
场
得分
10
场数
合计
负
胜
x
y
2x
y
16
2x+y=16
x+y=10
探究新知
思考一:上述方程有什么共同特点?
思考二:它与你学过的一元一次方程比较有什么区别?
思考三:你能给它起个名字吗?
x+y=10
2x+y=16
探究新知
含有两个未知数,并且所含未知数的项的次数都是1的方程叫作二元一次方程.
注意:
(1)“一次”是指含未知数的项的次数是1,而不是未知数的次数;
(2)方程的左右两边都是整式.
探究新知
(8)4xy+5=0
(1)x+y=11
(3)x2+y=5
(2)m+1=2
(4)3x-π=11
(5)
-5x=4y+2
(6)7+a=2b+11c
(7)7x+
=13
y
2
判断下列方程是不是二元一次方程?
是
是
不是
不是
不是
不是
不是
不是
探究新知
判断一个方程是否为二元一次方程的方法:
看原方程是否是整式方程且只含有两个未知数;
看整理化简后的方程是否具备两个未知数的系数都不为0,且含未知数的项的次数都是1.
探究新知
(1)已知:
5x3m+7-2y2n-1=4
是二元一次方程,则m=
,n=
。
(2)若mxy+9x+3yn-1=7是关于x,y的二元一次方程,则m
=
,n
=
。
-2
1
0
2
探究新知
例1
已知
|m-1|x
|m|+y2n-1=3
是二元一次方程,
则
m+n=________.
解析:根据题意得|m|=1且|m-1|≠0,2n-1=1,解得m=-1,n=1,所以m+n=0.
0
由方程是二元一次方程可知:
(1)未知数的系数不为0;(2)未知数的次数都是1.
探究新知
若
x2m-1+5y3n-2m
=7
是二元一次方程,则m=____,n=____.
2m-1=1
1
3n-2m=1
1
巩固练习
方程组中有两个未知数,含有每个未知数的项的次数都是1,并且一共有两个方程,像这样的方程组叫作二元一次方程组.
x+y=10
2x+y=16
叫作方程组
下列方程组是二元一次方程组的是(
)
探究新知
A.
B.
C.
B
D.
探究新知
二元一次方程组的解
【探究】满足课堂开始篮球联赛问题中的方程
,且符合问题的实际意义的值有哪些?把它们填入表中.
思考1 如果不考虑方程表示的实际意义,还可以取哪些值?
这些值是有限的吗?
x,y还可取到小数,如x=0.5,y=9.5;
有无数组这样的值.
x
y
x
0
1
2
3
4
5
6
7
8
9
10
y
10
9
8
7
6
5
4
3
2
1
0
探究新知
适合一个二元一次方程的一组未知数的值,
叫做这个二元一次方程的一个解.
探究新知
思考2 上表中哪对
x,y
的值还满足方程
2x+y=16
②?
x=6,x=4还满足方程
②.也就是说,
它是方程x+y=10
①与方程
②
的公共解,记作
二元一次方程组中各个方程的公共解,叫做这个二元一次方程组的解.
巩固练习
1.
下列各组数是不是方程
2a=3b+20
的解?
a=4
b=3
a=100
b=60
①
②
×
√
左边≠右边
右=3×3+20
右边=3×60+20
左边=2×100
左边=右边
左边=2×4
探究新知
一般地,二元一次方程有无数组解,而二元一次方程组只有一组解。
2.二元一次方程组
的解是(
)
{
x+2y=10,
y=2x
A.{
C.{
D.{
B.{
x=4,
y=3
x=3,
y=6
x=2,
y=4
x=4,
y=2
C
探究新知
{
x=-2,
y=3
例2
若
是方程x-ky=1的解,则k的值为
.
解析:将
代入原方程得
-2-3k=1,解得k=-1.
{
x=-2,
y=3
-1
探究新知
例3
加工某种产品须经两道工序,第一道工序每人每天可完成900件,第二道工序每人每天可完成1200件.现有7位工人参加这两道工序,应怎样安排人力,才能使每天第一、二道工序所完成的件数相等?请列出符合题意的二元一次方程组.
巩固练习
解:设安排第一道工序为x人,第二道工序为y人.
根据题意得
巩固练习
“一切问题都可以转化为数学问题,一切数学问题都可以转化为代数问题,而一切代数问题又都可以转化为方程问题,因此,一旦解决了方程问题,一切问题将迎刃而解!”
——法国数学家
笛卡儿[Descartes,
1596-1650
]
巩固练习
x+
=1,
y+x=2
1.下列不是二元一次方程组的是(
)
A.
x+y=3,
x-y=1
B.
C.
D.
6x+4y=9,
y=3x+4
B
x=1,
y=1
巩固练习
2.二元一次方程组
的解是(
)
A.
B.
C.
D.
C
x=1,
y=3
2x+y=5,
3x-2y=4
x=1,
y=2
x=2,
y=1
x=2,
y=-1
巩固练习
3.关于x、y的方程ax2+bx+2y=3是一个二元一次方程,则a、b的值分别为(
)
A
.a=0且
b=0
B.a=0或
b=0
C.
a=0且
b≠0
D.a≠0且
b≠0
C
4.
小刘同学用10元钱购买了两种不同的贺卡共8张,单价分别是1元与2元.设他购买了1元的贺卡x张,2元的贺卡y
张,那么可列方程组( )
巩固练习
D
A.
B.
C.
D.
6.若方程2x2m+3+3y3n-7=0
是关于x、y
的二元一次方程,则m=______,n=______;
巩固练习
5.已知
是方程2x-4y+2a=3的一组解,则a=____.
x=3,
y=1
1
2
-1
8
3
巩固练习
7.写出方程
x+2y=5
在自然数范围内的所有解.
x=1,
y=2
x=3,
y=1
x=5,
y=0
巩固练习
8.
把一根长13m的钢管截成2m长或3m长两种规格的钢管,怎样截不造成浪费?你有几种不同的截法?
解:设截成2m长的钢管x根,3m长的钢管y根,
则2x+3y=13,
∵x,y均为非负整数,∴
或
∴有2种不同的截法.
3m长1根、2m长5根以及3m长3根、2m长2根.
x=5,
y=1
x=2,
y=3
探究新知
认识二元一次方程组
二元一次方程及二元一次方程组的定义
二元一次方程及二元一次方程组的解
根据实际问题列二元一次方程组
1.二元一次方程的概念:每个方程都含有两个未知数(x和y),并且含有未知数的项的次数都是1,像这样的方程叫做二元一次方程。
2.二元一次方程组的概念:把具有相同未知数的两个二元一次方程合在一起,就组成了一个二元一次方程组。
3.二元一次方程的解的概念:一般地,使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解。
4.二元一次方程组的解的概念:一般地,二元一次方程组的两个方程的公共解,叫做二元一次方程组的解。
课堂小结
8.1
二元一次方程组
8
二元一次方程组
课时目标
1.了解二元一次方程,二元一次方程组及其解的概念,会检验所给的一组未知数的值是否是二元一次方程、二元一次方程组的解。
2.通过实例认识二元一次方程和二元一次方程组都是反映数量关系的重要数学模型,能设两个未知数并列方程组表示实际问题中的两种相关的等量关系。
探究新知
篮球联赛中,每场比赛都要分出胜负,每队胜1场得2分,负1场得1分。某队10场比赛中得到16分,那么这个队胜负场数应分别是多少?
探究新知
解:
设胜x场,则负(10-x)场,根据题意得方程
2x+(10-x)=16
解得
x=6
10-6=4
答:这个队胜6场,只负4场.
篮球联赛中,每场比赛都要分出胜负,每队胜1场得2分,负1场得1分。某队10场比赛中得到16分,那么这个队胜负场数应分别是多少?
探究新知
积分
场数
合计
负
胜
10
2x
y
16
等量关系有哪些?
那么,能设两个未知数吗?比如设胜x场,负y场;你能根据题意列出方程吗?
探究新知
胜的场数+负的场数=总场数
胜的场数的分数+负的场数的分数=总分数
设篮球队胜了x
场,负了y
场
得分
10
场数
合计
负
胜
x
y
2x
y
16
2x+y=16
x+y=10
探究新知
思考一:上述方程有什么共同特点?
思考二:它与你学过的一元一次方程比较有什么区别?
思考三:你能给它起个名字吗?
x+y=10
2x+y=16
探究新知
含有两个未知数,并且所含未知数的项的次数都是1的方程叫作二元一次方程.
注意:
(1)“一次”是指含未知数的项的次数是1,而不是未知数的次数;
(2)方程的左右两边都是整式.
探究新知
(8)4xy+5=0
(1)x+y=11
(3)x2+y=5
(2)m+1=2
(4)3x-π=11
(5)
-5x=4y+2
(6)7+a=2b+11c
(7)7x+
=13
y
2
判断下列方程是不是二元一次方程?
是
是
不是
不是
不是
不是
不是
不是
探究新知
判断一个方程是否为二元一次方程的方法:
看原方程是否是整式方程且只含有两个未知数;
看整理化简后的方程是否具备两个未知数的系数都不为0,且含未知数的项的次数都是1.
探究新知
(1)已知:
5x3m+7-2y2n-1=4
是二元一次方程,则m=
,n=
。
(2)若mxy+9x+3yn-1=7是关于x,y的二元一次方程,则m
=
,n
=
。
-2
1
0
2
探究新知
例1
已知
|m-1|x
|m|+y2n-1=3
是二元一次方程,
则
m+n=________.
解析:根据题意得|m|=1且|m-1|≠0,2n-1=1,解得m=-1,n=1,所以m+n=0.
0
由方程是二元一次方程可知:
(1)未知数的系数不为0;(2)未知数的次数都是1.
探究新知
若
x2m-1+5y3n-2m
=7
是二元一次方程,则m=____,n=____.
2m-1=1
1
3n-2m=1
1
巩固练习
方程组中有两个未知数,含有每个未知数的项的次数都是1,并且一共有两个方程,像这样的方程组叫作二元一次方程组.
x+y=10
2x+y=16
叫作方程组
下列方程组是二元一次方程组的是(
)
探究新知
A.
B.
C.
B
D.
探究新知
二元一次方程组的解
【探究】满足课堂开始篮球联赛问题中的方程
,且符合问题的实际意义的值有哪些?把它们填入表中.
思考1 如果不考虑方程表示的实际意义,还可以取哪些值?
这些值是有限的吗?
x,y还可取到小数,如x=0.5,y=9.5;
有无数组这样的值.
x
y
x
0
1
2
3
4
5
6
7
8
9
10
y
10
9
8
7
6
5
4
3
2
1
0
探究新知
适合一个二元一次方程的一组未知数的值,
叫做这个二元一次方程的一个解.
探究新知
思考2 上表中哪对
x,y
的值还满足方程
2x+y=16
②?
x=6,x=4还满足方程
②.也就是说,
它是方程x+y=10
①与方程
②
的公共解,记作
二元一次方程组中各个方程的公共解,叫做这个二元一次方程组的解.
巩固练习
1.
下列各组数是不是方程
2a=3b+20
的解?
a=4
b=3
a=100
b=60
①
②
×
√
左边≠右边
右=3×3+20
右边=3×60+20
左边=2×100
左边=右边
左边=2×4
探究新知
一般地,二元一次方程有无数组解,而二元一次方程组只有一组解。
2.二元一次方程组
的解是(
)
{
x+2y=10,
y=2x
A.{
C.{
D.{
B.{
x=4,
y=3
x=3,
y=6
x=2,
y=4
x=4,
y=2
C
探究新知
{
x=-2,
y=3
例2
若
是方程x-ky=1的解,则k的值为
.
解析:将
代入原方程得
-2-3k=1,解得k=-1.
{
x=-2,
y=3
-1
探究新知
例3
加工某种产品须经两道工序,第一道工序每人每天可完成900件,第二道工序每人每天可完成1200件.现有7位工人参加这两道工序,应怎样安排人力,才能使每天第一、二道工序所完成的件数相等?请列出符合题意的二元一次方程组.
巩固练习
解:设安排第一道工序为x人,第二道工序为y人.
根据题意得
巩固练习
“一切问题都可以转化为数学问题,一切数学问题都可以转化为代数问题,而一切代数问题又都可以转化为方程问题,因此,一旦解决了方程问题,一切问题将迎刃而解!”
——法国数学家
笛卡儿[Descartes,
1596-1650
]
巩固练习
x+
=1,
y+x=2
1.下列不是二元一次方程组的是(
)
A.
x+y=3,
x-y=1
B.
C.
D.
6x+4y=9,
y=3x+4
B
x=1,
y=1
巩固练习
2.二元一次方程组
的解是(
)
A.
B.
C.
D.
C
x=1,
y=3
2x+y=5,
3x-2y=4
x=1,
y=2
x=2,
y=1
x=2,
y=-1
巩固练习
3.关于x、y的方程ax2+bx+2y=3是一个二元一次方程,则a、b的值分别为(
)
A
.a=0且
b=0
B.a=0或
b=0
C.
a=0且
b≠0
D.a≠0且
b≠0
C
4.
小刘同学用10元钱购买了两种不同的贺卡共8张,单价分别是1元与2元.设他购买了1元的贺卡x张,2元的贺卡y
张,那么可列方程组( )
巩固练习
D
A.
B.
C.
D.
6.若方程2x2m+3+3y3n-7=0
是关于x、y
的二元一次方程,则m=______,n=______;
巩固练习
5.已知
是方程2x-4y+2a=3的一组解,则a=____.
x=3,
y=1
1
2
-1
8
3
巩固练习
7.写出方程
x+2y=5
在自然数范围内的所有解.
x=1,
y=2
x=3,
y=1
x=5,
y=0
巩固练习
8.
把一根长13m的钢管截成2m长或3m长两种规格的钢管,怎样截不造成浪费?你有几种不同的截法?
解:设截成2m长的钢管x根,3m长的钢管y根,
则2x+3y=13,
∵x,y均为非负整数,∴
或
∴有2种不同的截法.
3m长1根、2m长5根以及3m长3根、2m长2根.
x=5,
y=1
x=2,
y=3
探究新知
认识二元一次方程组
二元一次方程及二元一次方程组的定义
二元一次方程及二元一次方程组的解
根据实际问题列二元一次方程组
1.二元一次方程的概念:每个方程都含有两个未知数(x和y),并且含有未知数的项的次数都是1,像这样的方程叫做二元一次方程。
2.二元一次方程组的概念:把具有相同未知数的两个二元一次方程合在一起,就组成了一个二元一次方程组。
3.二元一次方程的解的概念:一般地,使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解。
4.二元一次方程组的解的概念:一般地,二元一次方程组的两个方程的公共解,叫做二元一次方程组的解。
课堂小结
