江西省南昌市进贤县第一中学2019-2020学年高二下学期开学考试数学试题(理)(word版含答案)
文档属性
| 名称 | 江西省南昌市进贤县第一中学2019-2020学年高二下学期开学考试数学试题(理)(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 834.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-27 22:34:25 | ||
图片预览



文档简介
(理科)数学试卷
第I卷(选择题)
一、单选题(每小题5分,共60分)
1.下列随机试验的结果,不能用离散型随机变量表示的是( )
A.将一枚均匀正方体骰子掷两次,所得点数之和
B.某篮球运动员6次罚球中投进的球数
C.电视机的使用寿命
D.从含有3件次品的50件产品中,任取2件,其中抽到次品的件数
2.已知下表为与之间的一组数据,若与线性相关,则与的回归直线必过点(
)
x
0
1
2
3
y
1
3
5
7
A.(2,2)
B.(1.5,0)
C.(1,2)
D.(1.5,4)
3.自2019年12月以来,在湖北省武汉市发现多起病毒性肺炎病例,研究表明,该新型冠状病毒具有很强的传染性各级政府反应迅速,采取了有效的防控阻击措施,把疫情控制在最低范围之内.某社区按上级要求做好在鄂返乡人员体格检查登记,有3个不同的住户属在鄂返乡住户,负责该小区体格检查的社区诊所共有4名医生,现要求这4名医生都要分配出去,且每个住户家里都要有医生去检查登记,则不同的分配方案共有(
)
A.12种
B.24种
C.36种
D.72种.
4.展开式中的系数为(
)
A.-7
B.28
C.35
D.42
5.如图所示,将四棱锥S-ABCD的每一个顶点染上一种颜色,并使同一条棱上的两端异色,如果只有5种色可供使用,则不同的染色方法种数为(
)
A.240
B.360
C.420
D.960
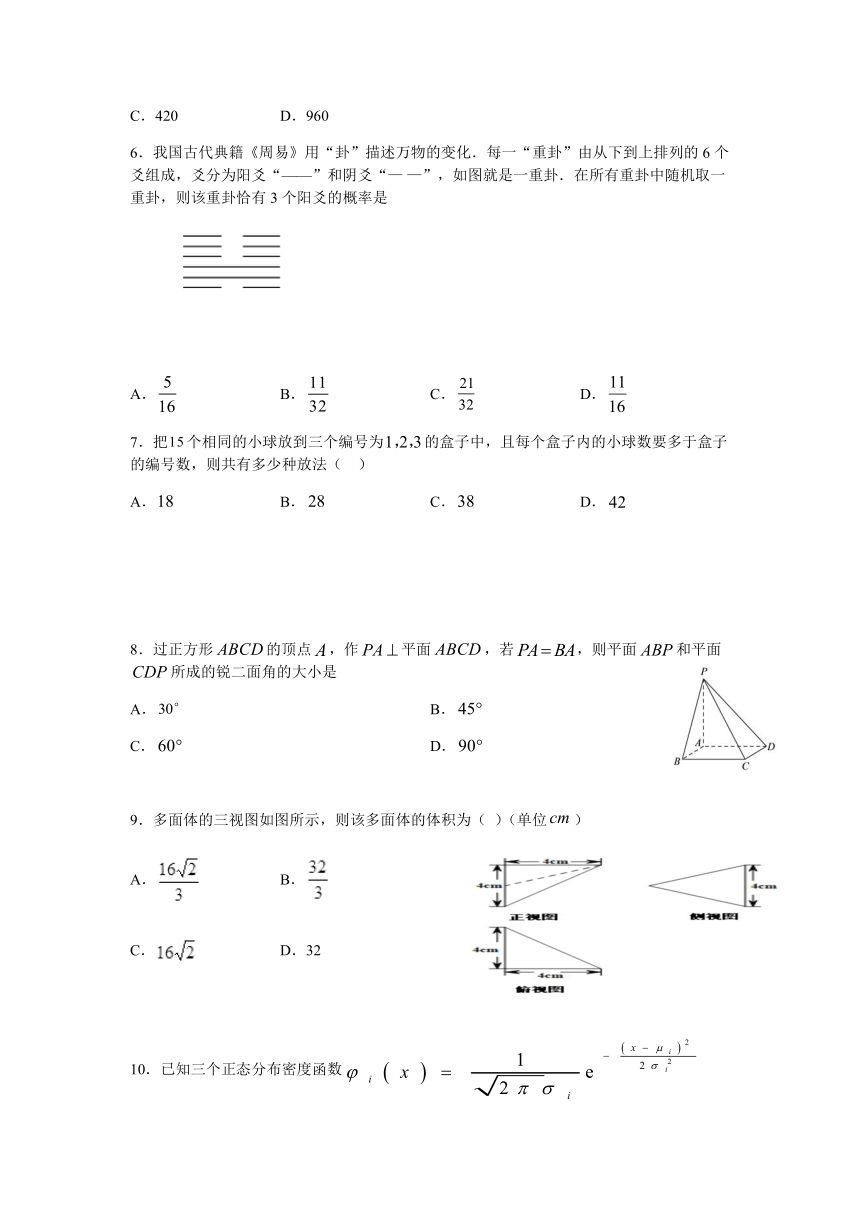
6.我国古代典籍《周易》用“卦”描述万物的变化.每一“重卦”由从下到上排列的6个爻组成,爻分为阳爻“——”和阴爻“—
—”,如图就是一重卦.在所有重卦中随机取一重卦,则该重卦恰有3个阳爻的概率是
A.
B.
C.
D.
7.把个相同的小球放到三个编号为的盒子中,且每个盒子内的小球数要多于盒子的编号数,则共有多少种放法(
)
A.
B.
C.
D.
8.过正方形的顶点,作平面,若,则平面和平面所成的锐二面角的大小是
A.
B.
C.
D.
9.多面体的三视图如图所示,则该多面体的体积为(
)(单位)
A.
B.
C.
D.32
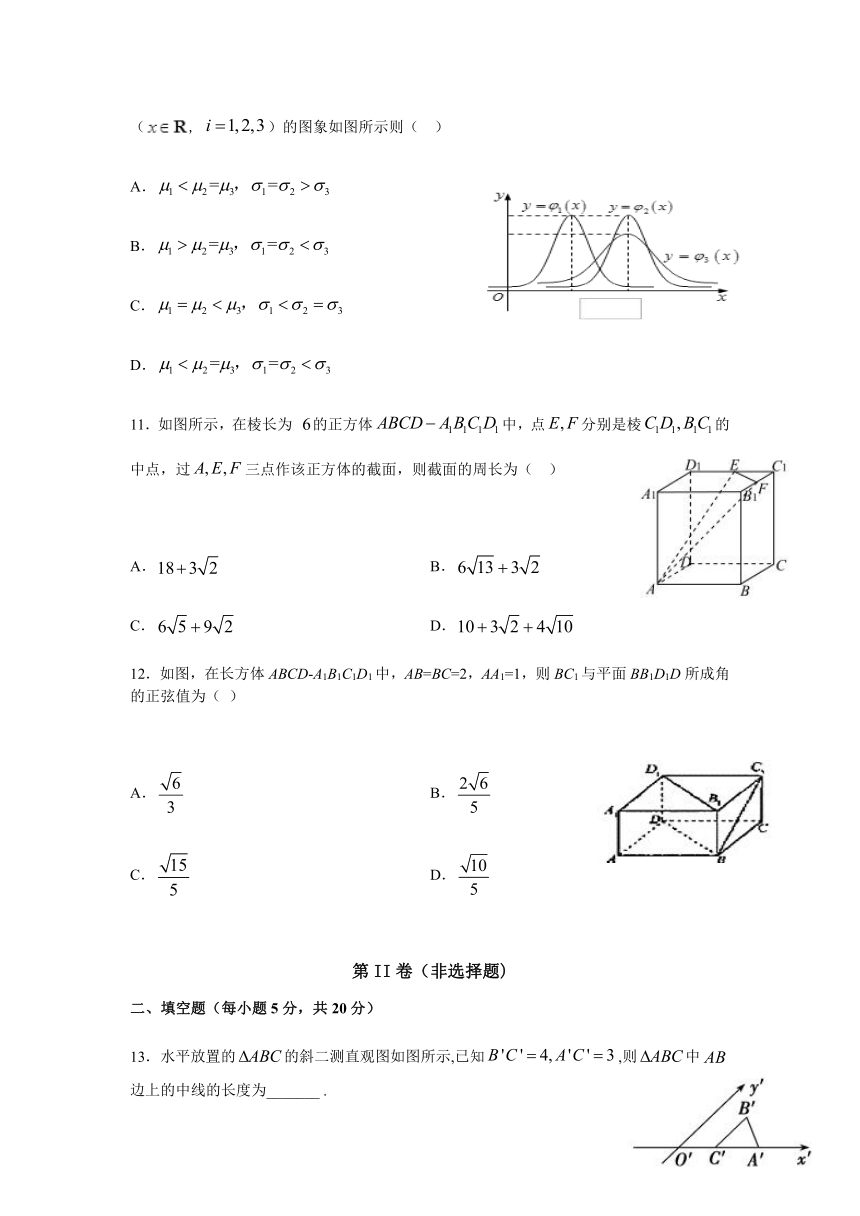
10.已知三个正态分布密度函数(,
)的图象如图所示则(
)
A.
B.
C.
D.
11.如图所示,在棱长为
的正方体中,点分别是棱的中点,过三点作该正方体的截面,则截面的周长为(
)
A.
B.
C.
D.
12.如图,在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1,则BC1与平面BB1D1D所成角的正弦值为(
)
A.
B.
C.
D.
第II卷(非选择题)
二、填空题(每小题5分,共20分)
13.水平放置的的斜二测直观图如图所示,已知,则中边上的中线的长度为_______
.
14.若多项式,则______.
15.在长方体中,底面是正方形,若,,则异面直线与所成的角的正切值为__________.
16.2020年初,我国突发新冠肺炎疫情.面对“突发灾难”,举国上下心,继解放军医疗队于除夕夜飞抵武汉,各省医疗队也陆续增援,纷纷投身疫情防控与病人救治之中.为分担“逆行者”的后顾之忧,某大学学生志愿者团队开展“爱心辅学”活动,为抗疫前线工作者子女在线辅导功课.现随机安排甲、乙、丙3名志愿者为某学生辅导数学、物理、化学、生物4门学科,每名志愿者至少辅导1门学科,每门学科由1名志愿者辅导,则数学学科恰好由甲辅导的概率为______.
三、解答题(17小题10分,18-22每小题12分共70分)
17.若的展开式的二项式系数和为128.
(1)求的值;
(2)求展开式中的常数项;
(3)求展开式中二项式系数的最大项.
18.如图是某直三棱柱被削去上底后所得几何体的左视图、俯视图、直观图,在直观图中,M是BD的中点,左视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
(Ⅰ)求该几何体的表面积和体积;
(Ⅱ)求点C到平面MAB的距离.
19.如图所示,
在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点,
(1)求证:
AC1//平面CDB1;
(2)求二面角C1-AB-C的平面角的正切值.
20.如图,在斜三棱柱中,已知,,且.
(Ⅰ)求证:平面平面;
(Ⅱ)若,求二面角的余弦值
.
21.继共享单车之后,又一种新型的出行方式------“共享汽车”也开始亮相南昌市,一款共享汽车在南昌提供的车型是“吉利”.每次租车收费按行驶里程加用车时间,标准是“1元/公里+0.1元/分钟”,李先生家离上班地点10公里,每次租用共享汽车上、下班,由于堵车因素,每次路上开车花费的时间是一个随机变量,根据一段时间统计40次路上开车花费时间在各时间段内的情况如下:
时间(分钟)
次数
8
14
8
8
2
以各时间段发生的频率视为概率,假设每次路上开车花费的时间视为用车时间,范围为分钟.
(1)若李先生上、下班时租用一次共享汽车路上开车不超过45分钟,便是所有可选择的交通工具中的一次最优选择,设是4次使用共享汽车中最优选择的次数,求的分布列和期望.
(2)若李先生每天上、下班均使用共享汽车,一个月(以20天计算)平均用车费用大约是多少(同一时段,用该区间的中点值作代表).
22.一商家诚邀甲、乙两名围棋高手进行一场网络国棋比赛,每比赛一局商家要向每名棋手支付2000元对局费,同时商家每局从转让网络转播权及广告宣传中获利12100元,从两名棋手以往比赛中得知,甲每局获胜的概率为,乙每局获胜的概率为,两名棋手约定:最多下五局,先连胜两局者获胜,比赛结束,比赛结束后,商家为获胜者颁发5000元的奖金,若没有决出获胜者则各颁发2500元.
(1)求下完五局且甲获胜的概率是多少;
(2)求商家从这场网络棋赛中获得的收益的数学期望是多少.
理科数学参考答案
1.C2.D3.C4.B5.C6.A7.B8.B9.B10.D11.B12.D
13.
首先根据直观图可知其平面图形为直角三角形,且两条直线边长为长,接下来利用勾股定理即可求出AB的长,然后利用直角三角形的性质进行解答即可.
【详解】
把直观图还原成平面图形如图所示:
得为直角三角形,且两条直角边的长,
由勾股定理可得,
故三角形AB边上的中线长为,
故答案是.
14.
由二项式定理及其展开式通项公式得展开式的通项为,令,解得,则,得解.
【详解】
由展开式的通项为,
令,解得,
则,
故答案为:.
15.
根据题意求出底面正方形的边长为2,所以长方体的高为1.然后根据两条异面直线所成角的定义作出与所成的角,通过解三角形的方法求出正切值.
【详解】
设,
由四边形是正方形可得.
因为底面,
所以,,
所以,
即,解得.
所以.
因为,
所以即异面直线与所成的角,
在中,,
所以异面直线与所成角的正切值为.
故答案为.
16.
根据题意,由排列组合公式分析3名志愿者辅导4门学科的情况数目,再分析其中甲辅导数学的情况数目,由古典概型公式计算可得答案.
【详解】
解:根据题意,要求甲、乙、丙3名志愿者每名志愿者至少辅导1门学科,
每门学科由1名志愿者辅导,则必有1人辅导2门学科;
则有种情况,
若甲辅导数学,有种情况,
则数学学科恰好由甲辅导的概率为,
故答案为:.
17.(1)
(2)
(3)
【解析】
试题分析:(1)二项式系数和为(2)求展开式的某一项需要首先找到展开式的代入相应的值求解(3)二项式系数最大的项为中间的一项或两项本题中展开后有8项,因此需求第4,5两项
试题解析:(1)
3分
(2),令,,常数项为
8分
(3)
12分
考点:二项式定理及展开式的性质
18.(Ⅰ)体积是4,表面积是;
(Ⅱ).
【解析】
试题分析:
(1)由题意得该几何体为四棱锥,然后根据三视图中的数据可得几何体的体积和表面积.(2)设C到面MAB的距离为,然后根据可得,即所求的点到面的距离.
试题解析:
由三视图可得,在几何体中,EA平面ABC,DC平面ABC,AE∥DC,AE=2,DC=4,
ABAC,且AC=2.
(Ⅰ)∵EA平面ABC,AB平面ABC,
∴EAAB,
又ABAC,,
∴AB平面ACDE,
∴四棱锥B—ACDE的高,
又梯形ACDE的面积,
∴体积为;
表面积为S=
.
(Ⅱ)如图,过M作MN⊥BC于N,过N作NH⊥AB于H,则MH⊥AB.
结合题意可得点M到AB的距离,
故.
设C到面MAB的距离为,
由得:
,
即
解得.即点C到平面MAB的距离.
19.(1)见解析;(3)
【解析】
【分析】
(1)连接DE,得DE∥AC1,由直线与平面平行的判定定理得AC1∥平面CDB1.
(2)过点C作AB的垂线CF交AB于点F,连C1F,得∠CFC1为C﹣AB﹣C1的平面角,得FC,在Rt△C1CF中得FC,解三角形即可求二面角C﹣AB﹣C1的正切值.
【详解】
(1)连接DE,由题意可知:DE为△ABC1的中位线,可知DE∥AC1,由
?AC1∥平面CDB.
(2)过点C作AB的垂线CF交AB于点F,连C1F,∵ABC﹣A1B1C1是直三棱柱,
∴CC1⊥AB,又由AB⊥CF且CC1∩CF=C,∴AB⊥平面CFC1,∴AB⊥FC1
于是有
?∠CFC1为C﹣AB﹣C1的平面角,在Rt△C1CF中得FC==.
在Rt△C1CF中,CC1=4,CF
.
∴二面角C﹣AB﹣C1的正切值为.
20.(1)见解析;(2)余弦值为.
(1)证明:连接,在平行四边形中,得,又,证得,利用线面垂直的判定定理得,进而得到平面平面.
(2)取的中点为坐标原点,建立空间直角坐标系,得到平和平面法向量,利用向量的夹角公式,即可求得二面角的余弦值.
【详解】
(1)证明:连接,在平行四边形中,
由得平行四边形为菱形,所以,
又,所以,所以,
又,所以,所以平面平面
(2)取的中点为坐标原点,建立空间直角坐标系,则的法向量为,
设面的法向量为,
因为,所以
由,令,则
设所求二面角为,则
故二面角的余弦值为.
21.(Ⅰ)见解析;(Ⅱ)542元.
【解析】
试题分析:(1)首先求为最优选择的概率是,故ξ的值可能为0,1,2,3,4,且ξ~B(4,),进而求得分布列和期望值;(2)根据题意得到每次花的平均时间为35.5,根据花的费用为10+35.5
0.1得到费用.
解析:
(Ⅰ)李先生一次租用共享汽车,为最优选择的概率
依题意ξ的值可能为0,1,2,3,4,且ξ~B(4,),
,
,
,
,
,
∴ξ的分布列为:
ξ
0
1
2
3
4
P
(或).
(Ⅱ)每次用车路上平均花的时间
(分钟)
每次租车的费用约为10+35.5×0.1=13.55元.
一个月的平均用车费用约为542元.
22.(1)(2)
(1)根据题意,连胜两局获胜.若比赛五局,且甲获胜,则五局的胜负情况为乙胜,甲胜,乙胜,甲胜,甲胜.进而由各自取胜的概率即可求解.
(2)根据题意可知,两人比赛局数可能的取值有.由所给取胜的概率,分别求得这四种情况下的概率,即可求得比赛局数的期望.扣除支出,即为商家获得的收益情况.
【详解】
(1)根据题意,先连胜两局者获胜.则下完五局甲获胜,这五局的胜负情况分别为:
乙胜,甲胜,乙胜,甲胜,甲胜.
甲每局获胜的概率为,乙每局获胜的概率为
所以下完五局甲获胜的概率为
(2)设为比赛的局数,表示商家获得的收益
则
由题意可知,可能的取值有
当比赛五局时,前四局两人各胜两局,且第五局无论谁胜商家都需支付5000元,因而
所以由离散型数学期望公式可得
故
所以商家从这场网络棋赛中获得的收益的数学期望是
第I卷(选择题)
一、单选题(每小题5分,共60分)
1.下列随机试验的结果,不能用离散型随机变量表示的是( )
A.将一枚均匀正方体骰子掷两次,所得点数之和
B.某篮球运动员6次罚球中投进的球数
C.电视机的使用寿命
D.从含有3件次品的50件产品中,任取2件,其中抽到次品的件数
2.已知下表为与之间的一组数据,若与线性相关,则与的回归直线必过点(
)
x
0
1
2
3
y
1
3
5
7
A.(2,2)
B.(1.5,0)
C.(1,2)
D.(1.5,4)
3.自2019年12月以来,在湖北省武汉市发现多起病毒性肺炎病例,研究表明,该新型冠状病毒具有很强的传染性各级政府反应迅速,采取了有效的防控阻击措施,把疫情控制在最低范围之内.某社区按上级要求做好在鄂返乡人员体格检查登记,有3个不同的住户属在鄂返乡住户,负责该小区体格检查的社区诊所共有4名医生,现要求这4名医生都要分配出去,且每个住户家里都要有医生去检查登记,则不同的分配方案共有(
)
A.12种
B.24种
C.36种
D.72种.
4.展开式中的系数为(
)
A.-7
B.28
C.35
D.42
5.如图所示,将四棱锥S-ABCD的每一个顶点染上一种颜色,并使同一条棱上的两端异色,如果只有5种色可供使用,则不同的染色方法种数为(
)
A.240
B.360
C.420
D.960
6.我国古代典籍《周易》用“卦”描述万物的变化.每一“重卦”由从下到上排列的6个爻组成,爻分为阳爻“——”和阴爻“—
—”,如图就是一重卦.在所有重卦中随机取一重卦,则该重卦恰有3个阳爻的概率是
A.
B.
C.
D.
7.把个相同的小球放到三个编号为的盒子中,且每个盒子内的小球数要多于盒子的编号数,则共有多少种放法(
)
A.
B.
C.
D.
8.过正方形的顶点,作平面,若,则平面和平面所成的锐二面角的大小是
A.
B.
C.
D.
9.多面体的三视图如图所示,则该多面体的体积为(
)(单位)
A.
B.
C.
D.32
10.已知三个正态分布密度函数(,
)的图象如图所示则(
)
A.
B.
C.
D.
11.如图所示,在棱长为
的正方体中,点分别是棱的中点,过三点作该正方体的截面,则截面的周长为(
)
A.
B.
C.
D.
12.如图,在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1,则BC1与平面BB1D1D所成角的正弦值为(
)
A.
B.
C.
D.
第II卷(非选择题)
二、填空题(每小题5分,共20分)
13.水平放置的的斜二测直观图如图所示,已知,则中边上的中线的长度为_______
.
14.若多项式,则______.
15.在长方体中,底面是正方形,若,,则异面直线与所成的角的正切值为__________.
16.2020年初,我国突发新冠肺炎疫情.面对“突发灾难”,举国上下心,继解放军医疗队于除夕夜飞抵武汉,各省医疗队也陆续增援,纷纷投身疫情防控与病人救治之中.为分担“逆行者”的后顾之忧,某大学学生志愿者团队开展“爱心辅学”活动,为抗疫前线工作者子女在线辅导功课.现随机安排甲、乙、丙3名志愿者为某学生辅导数学、物理、化学、生物4门学科,每名志愿者至少辅导1门学科,每门学科由1名志愿者辅导,则数学学科恰好由甲辅导的概率为______.
三、解答题(17小题10分,18-22每小题12分共70分)
17.若的展开式的二项式系数和为128.
(1)求的值;
(2)求展开式中的常数项;
(3)求展开式中二项式系数的最大项.
18.如图是某直三棱柱被削去上底后所得几何体的左视图、俯视图、直观图,在直观图中,M是BD的中点,左视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
(Ⅰ)求该几何体的表面积和体积;
(Ⅱ)求点C到平面MAB的距离.
19.如图所示,
在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点,
(1)求证:
AC1//平面CDB1;
(2)求二面角C1-AB-C的平面角的正切值.
20.如图,在斜三棱柱中,已知,,且.
(Ⅰ)求证:平面平面;
(Ⅱ)若,求二面角的余弦值
.
21.继共享单车之后,又一种新型的出行方式------“共享汽车”也开始亮相南昌市,一款共享汽车在南昌提供的车型是“吉利”.每次租车收费按行驶里程加用车时间,标准是“1元/公里+0.1元/分钟”,李先生家离上班地点10公里,每次租用共享汽车上、下班,由于堵车因素,每次路上开车花费的时间是一个随机变量,根据一段时间统计40次路上开车花费时间在各时间段内的情况如下:
时间(分钟)
次数
8
14
8
8
2
以各时间段发生的频率视为概率,假设每次路上开车花费的时间视为用车时间,范围为分钟.
(1)若李先生上、下班时租用一次共享汽车路上开车不超过45分钟,便是所有可选择的交通工具中的一次最优选择,设是4次使用共享汽车中最优选择的次数,求的分布列和期望.
(2)若李先生每天上、下班均使用共享汽车,一个月(以20天计算)平均用车费用大约是多少(同一时段,用该区间的中点值作代表).
22.一商家诚邀甲、乙两名围棋高手进行一场网络国棋比赛,每比赛一局商家要向每名棋手支付2000元对局费,同时商家每局从转让网络转播权及广告宣传中获利12100元,从两名棋手以往比赛中得知,甲每局获胜的概率为,乙每局获胜的概率为,两名棋手约定:最多下五局,先连胜两局者获胜,比赛结束,比赛结束后,商家为获胜者颁发5000元的奖金,若没有决出获胜者则各颁发2500元.
(1)求下完五局且甲获胜的概率是多少;
(2)求商家从这场网络棋赛中获得的收益的数学期望是多少.
理科数学参考答案
1.C2.D3.C4.B5.C6.A7.B8.B9.B10.D11.B12.D
13.
首先根据直观图可知其平面图形为直角三角形,且两条直线边长为长,接下来利用勾股定理即可求出AB的长,然后利用直角三角形的性质进行解答即可.
【详解】
把直观图还原成平面图形如图所示:
得为直角三角形,且两条直角边的长,
由勾股定理可得,
故三角形AB边上的中线长为,
故答案是.
14.
由二项式定理及其展开式通项公式得展开式的通项为,令,解得,则,得解.
【详解】
由展开式的通项为,
令,解得,
则,
故答案为:.
15.
根据题意求出底面正方形的边长为2,所以长方体的高为1.然后根据两条异面直线所成角的定义作出与所成的角,通过解三角形的方法求出正切值.
【详解】
设,
由四边形是正方形可得.
因为底面,
所以,,
所以,
即,解得.
所以.
因为,
所以即异面直线与所成的角,
在中,,
所以异面直线与所成角的正切值为.
故答案为.
16.
根据题意,由排列组合公式分析3名志愿者辅导4门学科的情况数目,再分析其中甲辅导数学的情况数目,由古典概型公式计算可得答案.
【详解】
解:根据题意,要求甲、乙、丙3名志愿者每名志愿者至少辅导1门学科,
每门学科由1名志愿者辅导,则必有1人辅导2门学科;
则有种情况,
若甲辅导数学,有种情况,
则数学学科恰好由甲辅导的概率为,
故答案为:.
17.(1)
(2)
(3)
【解析】
试题分析:(1)二项式系数和为(2)求展开式的某一项需要首先找到展开式的代入相应的值求解(3)二项式系数最大的项为中间的一项或两项本题中展开后有8项,因此需求第4,5两项
试题解析:(1)
3分
(2),令,,常数项为
8分
(3)
12分
考点:二项式定理及展开式的性质
18.(Ⅰ)体积是4,表面积是;
(Ⅱ).
【解析】
试题分析:
(1)由题意得该几何体为四棱锥,然后根据三视图中的数据可得几何体的体积和表面积.(2)设C到面MAB的距离为,然后根据可得,即所求的点到面的距离.
试题解析:
由三视图可得,在几何体中,EA平面ABC,DC平面ABC,AE∥DC,AE=2,DC=4,
ABAC,且AC=2.
(Ⅰ)∵EA平面ABC,AB平面ABC,
∴EAAB,
又ABAC,,
∴AB平面ACDE,
∴四棱锥B—ACDE的高,
又梯形ACDE的面积,
∴体积为;
表面积为S=
.
(Ⅱ)如图,过M作MN⊥BC于N,过N作NH⊥AB于H,则MH⊥AB.
结合题意可得点M到AB的距离,
故.
设C到面MAB的距离为,
由得:
,
即
解得.即点C到平面MAB的距离.
19.(1)见解析;(3)
【解析】
【分析】
(1)连接DE,得DE∥AC1,由直线与平面平行的判定定理得AC1∥平面CDB1.
(2)过点C作AB的垂线CF交AB于点F,连C1F,得∠CFC1为C﹣AB﹣C1的平面角,得FC,在Rt△C1CF中得FC,解三角形即可求二面角C﹣AB﹣C1的正切值.
【详解】
(1)连接DE,由题意可知:DE为△ABC1的中位线,可知DE∥AC1,由
?AC1∥平面CDB.
(2)过点C作AB的垂线CF交AB于点F,连C1F,∵ABC﹣A1B1C1是直三棱柱,
∴CC1⊥AB,又由AB⊥CF且CC1∩CF=C,∴AB⊥平面CFC1,∴AB⊥FC1
于是有
?∠CFC1为C﹣AB﹣C1的平面角,在Rt△C1CF中得FC==.
在Rt△C1CF中,CC1=4,CF
.
∴二面角C﹣AB﹣C1的正切值为.
20.(1)见解析;(2)余弦值为.
(1)证明:连接,在平行四边形中,得,又,证得,利用线面垂直的判定定理得,进而得到平面平面.
(2)取的中点为坐标原点,建立空间直角坐标系,得到平和平面法向量,利用向量的夹角公式,即可求得二面角的余弦值.
【详解】
(1)证明:连接,在平行四边形中,
由得平行四边形为菱形,所以,
又,所以,所以,
又,所以,所以平面平面
(2)取的中点为坐标原点,建立空间直角坐标系,则的法向量为,
设面的法向量为,
因为,所以
由,令,则
设所求二面角为,则
故二面角的余弦值为.
21.(Ⅰ)见解析;(Ⅱ)542元.
【解析】
试题分析:(1)首先求为最优选择的概率是,故ξ的值可能为0,1,2,3,4,且ξ~B(4,),进而求得分布列和期望值;(2)根据题意得到每次花的平均时间为35.5,根据花的费用为10+35.5
0.1得到费用.
解析:
(Ⅰ)李先生一次租用共享汽车,为最优选择的概率
依题意ξ的值可能为0,1,2,3,4,且ξ~B(4,),
,
,
,
,
,
∴ξ的分布列为:
ξ
0
1
2
3
4
P
(或).
(Ⅱ)每次用车路上平均花的时间
(分钟)
每次租车的费用约为10+35.5×0.1=13.55元.
一个月的平均用车费用约为542元.
22.(1)(2)
(1)根据题意,连胜两局获胜.若比赛五局,且甲获胜,则五局的胜负情况为乙胜,甲胜,乙胜,甲胜,甲胜.进而由各自取胜的概率即可求解.
(2)根据题意可知,两人比赛局数可能的取值有.由所给取胜的概率,分别求得这四种情况下的概率,即可求得比赛局数的期望.扣除支出,即为商家获得的收益情况.
【详解】
(1)根据题意,先连胜两局者获胜.则下完五局甲获胜,这五局的胜负情况分别为:
乙胜,甲胜,乙胜,甲胜,甲胜.
甲每局获胜的概率为,乙每局获胜的概率为
所以下完五局甲获胜的概率为
(2)设为比赛的局数,表示商家获得的收益
则
由题意可知,可能的取值有
当比赛五局时,前四局两人各胜两局,且第五局无论谁胜商家都需支付5000元,因而
所以由离散型数学期望公式可得
故
所以商家从这场网络棋赛中获得的收益的数学期望是
同课章节目录
