湘教版七年级数学下册 1.2.2 加减消元法课件(第2课时 共22张PPT)
文档属性
| 名称 | 湘教版七年级数学下册 1.2.2 加减消元法课件(第2课时 共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-27 08:20:11 | ||
图片预览







文档简介
(共22张PPT)
第2课时
选择适当方法解二元一次方程组
湘教版
七年级下册
学习目标
1.进一步了解用加减消元法解二元一次方程组;
2.会用加减法消元法解决相关问题.(重点)
问题1:消元法的基本思路?
问题2:说一说加减消元法的主要步骤.
二元
一元
加减消元:
(4)写解
写出方程组的解
(3)求解
求出两个未知数的值
(2)加减
消去一个元
(1)变形
同一个未知数的系数相同或互为相反数
导入新课
复习引入
相信自己
谁是英雄
(板书)
你能用哪些方法解下列方程组
解法一(代入法):
解:由①
得: ③
把③代入②得:
解得
把 代入③得
∴原方程组的解是
解法二(加减法)
解:①×2
得: ③
②×5得: ④
③
-④得:
解得
把 代入①得:
∴原方程组的解是
火眼金睛
以上两个方程组各用什么方法较简便?
(1) (2)
(1)用代入法(2)用加减法较简便.
你能体会这两种方法各自在什么情况下使用较方便吗?
总结:如果有一个未知数的系数为1或-1时,用代入法;如果同一个未知数的系数互为倍数,用加减法较为简便.
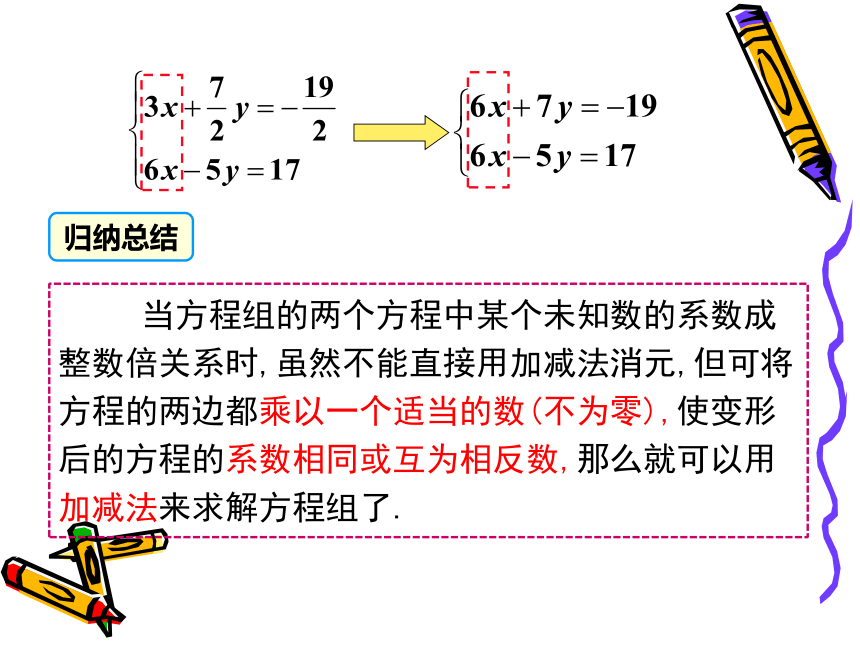
当方程组的两个方程中某个未知数的系数成整数倍关系时,虽然不能直接用加减法消元,但可将方程的两边都乘以一个适当的数(不为零),使变形后的方程的系数相同或互为相反数,那么就可以用加减法来求解方程组了.
归纳总结
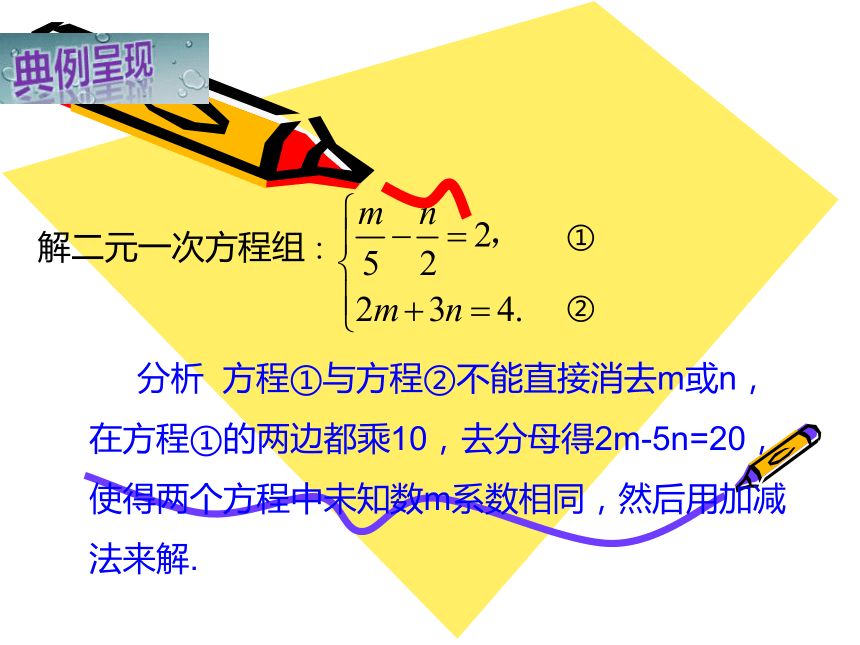
解二元一次方程组:
分析
方程①与方程②不能直接消去m或n,在方程①的两边都乘10,去分母得2m-5n=20,使得两个方程中未知数m系数相同,然后用加减法来解.
①
②
解
①X10,得2m-5n=20,
③
②-③,得
3n-(-5n)=4-20,
n=-2.
把n=-2代入②式得,2m+3X(-2)=4,
解得
m=5.
因此原方程的解是
方法总结
同一未知数的系数
时,利用等式的性质,使得未知数的系数
.
不相等也不互为相反数
相等或互为相反数
找系数的最小公倍数
解:由①×6-
②×4
得
2x+3y
-(2x
-
y)=4-8
y=
-1
把y=
-1代入②
解得
所以原方程组的解是
①
②
用加减消元法解方程组:
解二元一次方程组:
①
②
分析
为了使方程组中两个方程的未知数x的系数相同(或相反),可以在方程①的两边都乘4,在方程②的两边都乘3,然后将这两个方程相减,就可以将x消去.
解二元一次方程组
{
①
4x+3y=-1
②
解:①×4,得12x+16y=32
③
②×3,
得12x+9y=-3
④
③-
④,16y-9y=32-(-3)
解得
y=5
把y=5代入①式,得3x+4×5=-1
解得
x=-4
因此原方程组的解是
{
x=-4
y=5
3x+4y=8
在方程y=kx+b中,当x=1时,y=-1;当x=-1时,y=3,试求k和b的值.
分析
把x,y的两组值分别代入y=kx+b中,可得到一个关于k,b的二元一次方程组.
解:
根据题意得
①+②,得
2=2b,
解得
b=1.
把b=1代入①式,得
k=-2.
所以
.
①
②
解:解方程组
得
把
代入方程组
得解此方程组得
所以a2-2ab+b2=1.
例5
已知方程组
有相同的解,求a2
-2ab+b2的值.
用加减法解系数较复杂的二元一次方程组的应用
二
解:
①×2得
6x+4y=16
③
③-②得
9y=63
解得
y=7
把y=7代入①得
3x+2×7=
8
解得
x
=-2
因此原方程组的解是
1.用加减消元法解下列方程组:
(1)
①
②
当堂练习
解:
①×4得
12x+16y=44
③
②×3得
12x-15y=-111
④
③-④
得
31y=155
解得
y=5
把y=5代入①
得
3x+4×5=
11
解得
x
=-3
因此原方程组的一个解是
(2)
①
②
解:
①×5得
10x-25y=120
③
②×2得
10x
+4y
=
62
④
③-④得
-29y=58
解得
y=-2
把y=-2代入①
得
2x-5×(-2)=
24
解得
x
=7
因此原方程组的一个解是
(3)
①
②
回顾本节课的学习过程,回答以下问题:
(1)结合例题,谈一谈列方程组解决实际问题时应注意什么?
(2)代入消元法和加减消元法有什么联系与区别?如何选择方法运算更简便?
知识梳理
谢谢,请提出宝贵意见!
第2课时
选择适当方法解二元一次方程组
湘教版
七年级下册
学习目标
1.进一步了解用加减消元法解二元一次方程组;
2.会用加减法消元法解决相关问题.(重点)
问题1:消元法的基本思路?
问题2:说一说加减消元法的主要步骤.
二元
一元
加减消元:
(4)写解
写出方程组的解
(3)求解
求出两个未知数的值
(2)加减
消去一个元
(1)变形
同一个未知数的系数相同或互为相反数
导入新课
复习引入
相信自己
谁是英雄
(板书)
你能用哪些方法解下列方程组
解法一(代入法):
解:由①
得: ③
把③代入②得:
解得
把 代入③得
∴原方程组的解是
解法二(加减法)
解:①×2
得: ③
②×5得: ④
③
-④得:
解得
把 代入①得:
∴原方程组的解是
火眼金睛
以上两个方程组各用什么方法较简便?
(1) (2)
(1)用代入法(2)用加减法较简便.
你能体会这两种方法各自在什么情况下使用较方便吗?
总结:如果有一个未知数的系数为1或-1时,用代入法;如果同一个未知数的系数互为倍数,用加减法较为简便.
当方程组的两个方程中某个未知数的系数成整数倍关系时,虽然不能直接用加减法消元,但可将方程的两边都乘以一个适当的数(不为零),使变形后的方程的系数相同或互为相反数,那么就可以用加减法来求解方程组了.
归纳总结
解二元一次方程组:
分析
方程①与方程②不能直接消去m或n,在方程①的两边都乘10,去分母得2m-5n=20,使得两个方程中未知数m系数相同,然后用加减法来解.
①
②
解
①X10,得2m-5n=20,
③
②-③,得
3n-(-5n)=4-20,
n=-2.
把n=-2代入②式得,2m+3X(-2)=4,
解得
m=5.
因此原方程的解是
方法总结
同一未知数的系数
时,利用等式的性质,使得未知数的系数
.
不相等也不互为相反数
相等或互为相反数
找系数的最小公倍数
解:由①×6-
②×4
得
2x+3y
-(2x
-
y)=4-8
y=
-1
把y=
-1代入②
解得
所以原方程组的解是
①
②
用加减消元法解方程组:
解二元一次方程组:
①
②
分析
为了使方程组中两个方程的未知数x的系数相同(或相反),可以在方程①的两边都乘4,在方程②的两边都乘3,然后将这两个方程相减,就可以将x消去.
解二元一次方程组
{
①
4x+3y=-1
②
解:①×4,得12x+16y=32
③
②×3,
得12x+9y=-3
④
③-
④,16y-9y=32-(-3)
解得
y=5
把y=5代入①式,得3x+4×5=-1
解得
x=-4
因此原方程组的解是
{
x=-4
y=5
3x+4y=8
在方程y=kx+b中,当x=1时,y=-1;当x=-1时,y=3,试求k和b的值.
分析
把x,y的两组值分别代入y=kx+b中,可得到一个关于k,b的二元一次方程组.
解:
根据题意得
①+②,得
2=2b,
解得
b=1.
把b=1代入①式,得
k=-2.
所以
.
①
②
解:解方程组
得
把
代入方程组
得解此方程组得
所以a2-2ab+b2=1.
例5
已知方程组
有相同的解,求a2
-2ab+b2的值.
用加减法解系数较复杂的二元一次方程组的应用
二
解:
①×2得
6x+4y=16
③
③-②得
9y=63
解得
y=7
把y=7代入①得
3x+2×7=
8
解得
x
=-2
因此原方程组的解是
1.用加减消元法解下列方程组:
(1)
①
②
当堂练习
解:
①×4得
12x+16y=44
③
②×3得
12x-15y=-111
④
③-④
得
31y=155
解得
y=5
把y=5代入①
得
3x+4×5=
11
解得
x
=-3
因此原方程组的一个解是
(2)
①
②
解:
①×5得
10x-25y=120
③
②×2得
10x
+4y
=
62
④
③-④得
-29y=58
解得
y=-2
把y=-2代入①
得
2x-5×(-2)=
24
解得
x
=7
因此原方程组的一个解是
(3)
①
②
回顾本节课的学习过程,回答以下问题:
(1)结合例题,谈一谈列方程组解决实际问题时应注意什么?
(2)代入消元法和加减消元法有什么联系与区别?如何选择方法运算更简便?
知识梳理
谢谢,请提出宝贵意见!
