人教版七年级数学下册 8.2消元---解二元一次方程组课件(共32张PPT)
文档属性
| 名称 | 人教版七年级数学下册 8.2消元---解二元一次方程组课件(共32张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 278.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-27 00:00:00 | ||
图片预览











文档简介
(共32张PPT)
七年级数学下册第八章
二元一次方程组
8.2
解二元一次方程组
巩固与提升
1.了解解方程组的基本思想是消元.
2.了解代入法是消元的一种方法,灵活运用代入法解二元一次方程组.
重点:用代入法解二元一次方程组的消元过程.
难点:用代入法解较复杂的二元一次方程组.
学习目标(一)
重点
难点
1.理解加减消元法.
2.会用加减消元法解二元一次方程组.
重点:掌握用加减消元法解二元一次方程组的方法.
难点:灵活地对方程进行恒等变形,使之便于加减消元.
学习目标(二)
重点
难点
知识点(一)
代入消元法
消元思想
二元一次方程组中有两个未知数,如果消去其中一个未知数,那么就把二元一次方程组转化为我们熟悉的一元一次方程,我们可以先求出一个未知数,然后再求另一个未知数,这种将未知数的个数由多化少、逐一解决的思想,叫做消元思想.
代入消元法
把二元一次方程组中一个方程组中一个方程的一个未知数用含另一个未知数的式子表示出来,再代入另一个方程,实现消元,进而求得这个二元一次方程组的解.这种方法叫做代入消元法,简称代入法.
一般步骤
①从方程组中选定一个系数比较简单的方程进行变形,用含有x(或y)的代数式表示y(或x),即变成y=ax+b(或x=ay+b)的形式;
②将y=ax+b或x=ay+b代入另一个方程中,消去y(或x)得到一个关于x(或y)的一元一次方程;
③解这个一元一次方程,求出x(或y)的值;
④把求得的x(或y)的值代入y=ax+b(或x=ay+b)中,求出y(或x)的值;
⑤把求得的x、y的值用“{”联立起来,就是方程组的解.
x
-
y
=
3
,
3
x
-
8
y
=
14.
转化
代入
求解
回代
写解
①
②
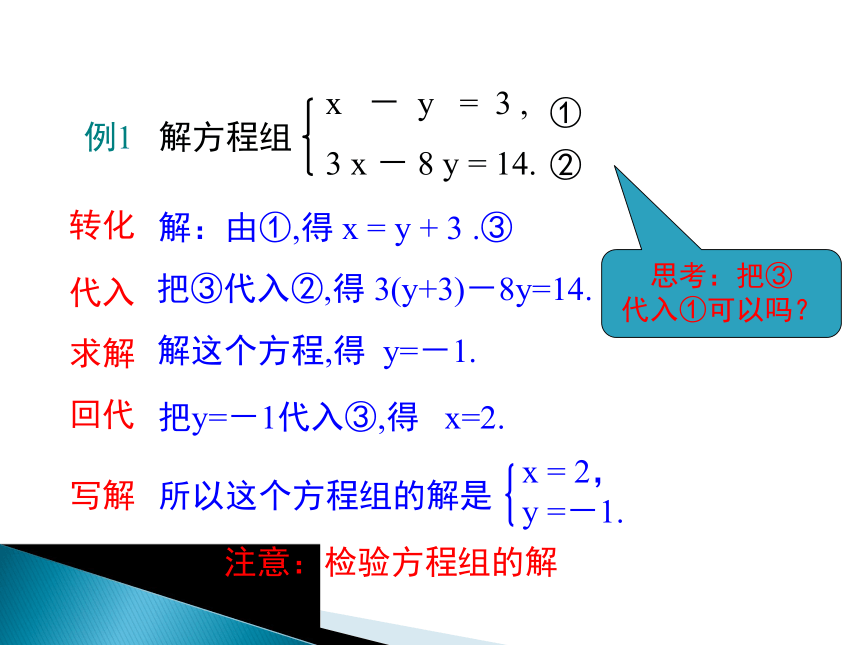
所以这个方程组的解是
x
=
2,
y
=-1.
把y=-1代入③,得
x=2.
把③代入②,得
3(y+3)-8y=14.
解:由①,得
x
=
y
+
3
.③
注意:检验方程组的解
例1
解方程组
解这个方程,得
y=-1.
思考:把③
代入①可以吗?
观察上面的方程和方程组,你能发现二者之间的联系吗?请你尝试求得方程组的解。(先试着独立完成,然后与你的同伴交流做法)
1.为什么能替换?
代表了同一个量
二元一次方程组
一元一次方程
消元
2.代入前后的方程组发生了怎样的变化?(代入的作用)
化归思想
代入
解:
由②得,
x=
y=-1.
①
②
①
②
把③代入①得,
解得y=-1,
把y=-1代入③得,
所以这个方程组的解为:
解:
由②得,
把③代入①得,
解得x=-3,
把x=-3代入③得,
x=-3
y=
所以这个方程组的解为:
练一练:解方程组
例2:
若方程5x
2m+n
+
4y
3m-2n
=
9是关于x、y的二元一次方程,求m
、n
的值.
解:
根据已知条件可列方程组:
2m
+
n
=
1
3m
–
2n
=
1
①
②
由①得
把③代入②得:
n
=
1
–2m
③
3m
–
2(1
–
2m)=
1
把m
代入③,得:
例3:李大叔去年承包了10亩地种植甲、乙两种蔬菜,共获利18000元,其中甲种蔬菜每亩获利2000元,乙种
蔬菜每亩获利1500元,李大叔去年甲、乙两种蔬菜各种植了多少亩?
解:
设甲、乙两种蔬菜各种植了x、y亩,依题意得:
x+y=10
①
2000x+1500y=18000
②
由①得
y=10-x
.
③
将③代入②,得
2000x+1500(10-x)=18000
.
解得
x=6.
将x=6代入③,得y=4.
答:李大叔去年甲、乙两种蔬菜各种植了6亩、4亩.
拓展题(1)
1、已知a、b满足方程组
3
2、若单项式-3x2y2m+n与2xm+ny4是同类项,则m2+2mn的算术平方根为(
)
2
知识点(二)
加减消元法
当二元一次方程组的两个方程中同一未知数的系数相反或相等时,把这两个方程的两边分别相加或相减,就能消去这个未知数,得到一个一元一次方程.这种方法叫做加减消元法,简称加减法.
用加减法解二元一次方程组的一般步骤
①根据“方程两边都乘(或除以)同一个不等于0的数,所得方程与原方程是同解方程”的原理,将原方程组化成有一个未知数的系数的绝对值相等的形式,即同一个未知数的系数相等或互为相反数;
②根据“方程两边都加上(或减去)同一个数,所得方程与原方程是同解方程”的原理,将变形后的两个方程相加(或相减),消去一个未知数,得到一个一元一次方程;
③解这个一元一次方程,得到一个未知数的值;
④将求出的未知数的值代入原方程组的任意一个方程中,求出另一个未知数,从而得到方程组的解;
⑤将两个未知数的值用“{”联立起来,就是方程组的解.
例4:用加减法解下列方程组:
解:
②-①,得8y=-8,即y=-1.
2x-5y=7
3y+2x=-1;
②×3,得51x-9y=222
③
解之得x=-1,
所以方程组的解为
x=1
y=-1.
(1)
8x+9y=73
17x-3y=74;
(2)
2x-5y=7
①
3y+2x=-1;
②
(1)
把y=-1代入①,得2x+5=7,
8x+9y=73
①
17x-3y=74;
②
(2)
①+③,得59x=295,解得x=5.
把x=5代入①,得8×5+9y=73,
解得y=
所以原方程组的解是
x=5
y=
①
②
例5:解方程组
解:由①
+
②,得
4(x+y)=36
所以
x+y=9
③
由①
-
②,得
6(x-y)=24
所以
x-y=4
④
解由③④组成的方程组
解得
法二:
整理得
总结区:整体代入法(换元法)是数学中的重要方法之一,这种方法往往能使运算更简便.
例6:用多种方法解方程组:
点拨:一般方法:可将方程组化简成一般形式,用代入法或加减法解方程组;
特殊方法:可将x+y,x-y分别作为一个整体,用换元法解.
解法一(代入法):方程组化简,得
由①,得y=5x-36.③
把③代入②,得x+5(5x-36)=28,解得x=8.
把x=8代入③,得y=4.
所以原方程组的解为
解法二(加减法):
方程组化简,得
①×5+②,得26x=208,x=8.
把x=8代入①,得40-y=36,y=4.
所以原方程组的解为
解法三(换元法):
设x+y=m,x-y=n,则原方程组可变为:
由①得2m+3n=36.③
③×2+②×3,得13m=156,故m=12.
把m=12代入②,解得n=4.
于是可得方程组解得
①
②
解得
例7:一批机器零件共1100个,如果甲先做5天后,乙加入合做,再做8天正好完成;如果乙先做5天后,甲加入合做,再做9天恰好完成,问两人每天各做多少个零件?
解析:
找出等量关系:甲先做5天的零件+甲乙合做8天的零件=1100,乙先做5天的零件+甲乙合做9天的零件=1100,列出方程组求解.
解:
设甲每天做x个零件,乙每天做y个零件,根据题意,得
5x+8(x+y)=1100
5y+9(x+y)=1100,
整理得
①×7,得91x+56y=7700,③
13x+8y=1100
①
9x+14y=1100
②,
②×4,得36x+56y=4400,④
③-④,得55x=3300,
解这个方程得x=60.
把x=60代入②,得y=40.
所以这个方程组的解是
x=60
y=40.
答:甲每天做60个零件,乙每天做40个零件.
1、.已知x、y满足方程组
求代数式x-y的值.
解:
②-①得2x-2y=-1-5,
得x-y=-3.
①
②
练一练
已知
,
则a+b等于_____.
3
①
②
分析:方法一:直接解方程组,求出a与b的值,然后就可以求出a+b.
方法二:?+?得
4a+4b=12,
a+b=3.
总结区:解题的关键是观察两个方程相同未知数的系数关系,利用加减消元法求解.
2辆大卡车和5辆小卡车工作2小时可运送垃圾36吨,3辆大卡车和2辆小卡车工作5小时可运输垃圾80
吨,
那么1辆大卡车和1辆小卡车每小时各运多少吨垃圾?
解:设1辆大卡车和1辆小卡车每小时各运x吨和y吨垃圾.
根据题意可得方程组:
化简可得:
①
②
②-①得
11x=44,解得x=4.
将x=4代入①可得y=2.
因此这个方程组的解为
.
答:1辆大卡车和1辆小卡车每小时各运4吨和2吨垃圾.
解二元一次方程组常用的数学思想
整体思想:在解方程组时可起到事半功倍的效果,在解方程组之前,同学们要仔细观察系数的特点.
例8:先阅读,再解方程组.
解方程组
可由①得x-y=1,③ 然后将③代入②,
得4×1-y=5,解得y=-1.
把y=-1代入③,得x=0.
①
②
所以原方程组的解为
“整体代入法”
请用此方法解方程组:
由①,得2x-3y=2.③
把③代入②,得1+2y=9,解得y=4.
把y=4代入③,得x=7.
解:
所以原方程组的解为
①
②
例9:解方程组:
当未知数是“多项式”时,可以把其用其他字母代替,即用转化为新的方程组来求解.
解:设x+y=a,x-y=b,则原方程组可化为
解得
所以x+y=6,x-y=20.
将它们组成新方程组,即
解得
例10:解方程组:
解:②-①,得x+y=1.③
由③得y=1-x.④
将④代入②,得2
020x+2
021(1-x)=2022,解得x=-1.
①
②
将x=-1代入④,得y=1-(-1)=2.
所以原方程组的解为
例11:解方程组:
解:①+②,得10
000x-10
000y=50
000,即x-y=5.③
①-②,得6
718x+6
718y=6
718,即x+y=1.④
③+④,得2x=6,解得x=3;
③-④,得-2y=4,解得y=-2.
①
②
所以原方程组的解为
拓展题(2)
1.若
,
则x+2y=
______
2.已知2ayb3x+1与-3ax-2b2-2y是同类项,则x
=
,y=__
_
-3
1
-1
3、若
,
则x,y的值为(
)
x=1,y=1
家庭作业
请完成课后相关练习。
七年级数学下册第八章
二元一次方程组
8.2
解二元一次方程组
巩固与提升
1.了解解方程组的基本思想是消元.
2.了解代入法是消元的一种方法,灵活运用代入法解二元一次方程组.
重点:用代入法解二元一次方程组的消元过程.
难点:用代入法解较复杂的二元一次方程组.
学习目标(一)
重点
难点
1.理解加减消元法.
2.会用加减消元法解二元一次方程组.
重点:掌握用加减消元法解二元一次方程组的方法.
难点:灵活地对方程进行恒等变形,使之便于加减消元.
学习目标(二)
重点
难点
知识点(一)
代入消元法
消元思想
二元一次方程组中有两个未知数,如果消去其中一个未知数,那么就把二元一次方程组转化为我们熟悉的一元一次方程,我们可以先求出一个未知数,然后再求另一个未知数,这种将未知数的个数由多化少、逐一解决的思想,叫做消元思想.
代入消元法
把二元一次方程组中一个方程组中一个方程的一个未知数用含另一个未知数的式子表示出来,再代入另一个方程,实现消元,进而求得这个二元一次方程组的解.这种方法叫做代入消元法,简称代入法.
一般步骤
①从方程组中选定一个系数比较简单的方程进行变形,用含有x(或y)的代数式表示y(或x),即变成y=ax+b(或x=ay+b)的形式;
②将y=ax+b或x=ay+b代入另一个方程中,消去y(或x)得到一个关于x(或y)的一元一次方程;
③解这个一元一次方程,求出x(或y)的值;
④把求得的x(或y)的值代入y=ax+b(或x=ay+b)中,求出y(或x)的值;
⑤把求得的x、y的值用“{”联立起来,就是方程组的解.
x
-
y
=
3
,
3
x
-
8
y
=
14.
转化
代入
求解
回代
写解
①
②
所以这个方程组的解是
x
=
2,
y
=-1.
把y=-1代入③,得
x=2.
把③代入②,得
3(y+3)-8y=14.
解:由①,得
x
=
y
+
3
.③
注意:检验方程组的解
例1
解方程组
解这个方程,得
y=-1.
思考:把③
代入①可以吗?
观察上面的方程和方程组,你能发现二者之间的联系吗?请你尝试求得方程组的解。(先试着独立完成,然后与你的同伴交流做法)
1.为什么能替换?
代表了同一个量
二元一次方程组
一元一次方程
消元
2.代入前后的方程组发生了怎样的变化?(代入的作用)
化归思想
代入
解:
由②得,
x=
y=-1.
①
②
①
②
把③代入①得,
解得y=-1,
把y=-1代入③得,
所以这个方程组的解为:
解:
由②得,
把③代入①得,
解得x=-3,
把x=-3代入③得,
x=-3
y=
所以这个方程组的解为:
练一练:解方程组
例2:
若方程5x
2m+n
+
4y
3m-2n
=
9是关于x、y的二元一次方程,求m
、n
的值.
解:
根据已知条件可列方程组:
2m
+
n
=
1
3m
–
2n
=
1
①
②
由①得
把③代入②得:
n
=
1
–2m
③
3m
–
2(1
–
2m)=
1
把m
代入③,得:
例3:李大叔去年承包了10亩地种植甲、乙两种蔬菜,共获利18000元,其中甲种蔬菜每亩获利2000元,乙种
蔬菜每亩获利1500元,李大叔去年甲、乙两种蔬菜各种植了多少亩?
解:
设甲、乙两种蔬菜各种植了x、y亩,依题意得:
x+y=10
①
2000x+1500y=18000
②
由①得
y=10-x
.
③
将③代入②,得
2000x+1500(10-x)=18000
.
解得
x=6.
将x=6代入③,得y=4.
答:李大叔去年甲、乙两种蔬菜各种植了6亩、4亩.
拓展题(1)
1、已知a、b满足方程组
3
2、若单项式-3x2y2m+n与2xm+ny4是同类项,则m2+2mn的算术平方根为(
)
2
知识点(二)
加减消元法
当二元一次方程组的两个方程中同一未知数的系数相反或相等时,把这两个方程的两边分别相加或相减,就能消去这个未知数,得到一个一元一次方程.这种方法叫做加减消元法,简称加减法.
用加减法解二元一次方程组的一般步骤
①根据“方程两边都乘(或除以)同一个不等于0的数,所得方程与原方程是同解方程”的原理,将原方程组化成有一个未知数的系数的绝对值相等的形式,即同一个未知数的系数相等或互为相反数;
②根据“方程两边都加上(或减去)同一个数,所得方程与原方程是同解方程”的原理,将变形后的两个方程相加(或相减),消去一个未知数,得到一个一元一次方程;
③解这个一元一次方程,得到一个未知数的值;
④将求出的未知数的值代入原方程组的任意一个方程中,求出另一个未知数,从而得到方程组的解;
⑤将两个未知数的值用“{”联立起来,就是方程组的解.
例4:用加减法解下列方程组:
解:
②-①,得8y=-8,即y=-1.
2x-5y=7
3y+2x=-1;
②×3,得51x-9y=222
③
解之得x=-1,
所以方程组的解为
x=1
y=-1.
(1)
8x+9y=73
17x-3y=74;
(2)
2x-5y=7
①
3y+2x=-1;
②
(1)
把y=-1代入①,得2x+5=7,
8x+9y=73
①
17x-3y=74;
②
(2)
①+③,得59x=295,解得x=5.
把x=5代入①,得8×5+9y=73,
解得y=
所以原方程组的解是
x=5
y=
①
②
例5:解方程组
解:由①
+
②,得
4(x+y)=36
所以
x+y=9
③
由①
-
②,得
6(x-y)=24
所以
x-y=4
④
解由③④组成的方程组
解得
法二:
整理得
总结区:整体代入法(换元法)是数学中的重要方法之一,这种方法往往能使运算更简便.
例6:用多种方法解方程组:
点拨:一般方法:可将方程组化简成一般形式,用代入法或加减法解方程组;
特殊方法:可将x+y,x-y分别作为一个整体,用换元法解.
解法一(代入法):方程组化简,得
由①,得y=5x-36.③
把③代入②,得x+5(5x-36)=28,解得x=8.
把x=8代入③,得y=4.
所以原方程组的解为
解法二(加减法):
方程组化简,得
①×5+②,得26x=208,x=8.
把x=8代入①,得40-y=36,y=4.
所以原方程组的解为
解法三(换元法):
设x+y=m,x-y=n,则原方程组可变为:
由①得2m+3n=36.③
③×2+②×3,得13m=156,故m=12.
把m=12代入②,解得n=4.
于是可得方程组解得
①
②
解得
例7:一批机器零件共1100个,如果甲先做5天后,乙加入合做,再做8天正好完成;如果乙先做5天后,甲加入合做,再做9天恰好完成,问两人每天各做多少个零件?
解析:
找出等量关系:甲先做5天的零件+甲乙合做8天的零件=1100,乙先做5天的零件+甲乙合做9天的零件=1100,列出方程组求解.
解:
设甲每天做x个零件,乙每天做y个零件,根据题意,得
5x+8(x+y)=1100
5y+9(x+y)=1100,
整理得
①×7,得91x+56y=7700,③
13x+8y=1100
①
9x+14y=1100
②,
②×4,得36x+56y=4400,④
③-④,得55x=3300,
解这个方程得x=60.
把x=60代入②,得y=40.
所以这个方程组的解是
x=60
y=40.
答:甲每天做60个零件,乙每天做40个零件.
1、.已知x、y满足方程组
求代数式x-y的值.
解:
②-①得2x-2y=-1-5,
得x-y=-3.
①
②
练一练
已知
,
则a+b等于_____.
3
①
②
分析:方法一:直接解方程组,求出a与b的值,然后就可以求出a+b.
方法二:?+?得
4a+4b=12,
a+b=3.
总结区:解题的关键是观察两个方程相同未知数的系数关系,利用加减消元法求解.
2辆大卡车和5辆小卡车工作2小时可运送垃圾36吨,3辆大卡车和2辆小卡车工作5小时可运输垃圾80
吨,
那么1辆大卡车和1辆小卡车每小时各运多少吨垃圾?
解:设1辆大卡车和1辆小卡车每小时各运x吨和y吨垃圾.
根据题意可得方程组:
化简可得:
①
②
②-①得
11x=44,解得x=4.
将x=4代入①可得y=2.
因此这个方程组的解为
.
答:1辆大卡车和1辆小卡车每小时各运4吨和2吨垃圾.
解二元一次方程组常用的数学思想
整体思想:在解方程组时可起到事半功倍的效果,在解方程组之前,同学们要仔细观察系数的特点.
例8:先阅读,再解方程组.
解方程组
可由①得x-y=1,③ 然后将③代入②,
得4×1-y=5,解得y=-1.
把y=-1代入③,得x=0.
①
②
所以原方程组的解为
“整体代入法”
请用此方法解方程组:
由①,得2x-3y=2.③
把③代入②,得1+2y=9,解得y=4.
把y=4代入③,得x=7.
解:
所以原方程组的解为
①
②
例9:解方程组:
当未知数是“多项式”时,可以把其用其他字母代替,即用转化为新的方程组来求解.
解:设x+y=a,x-y=b,则原方程组可化为
解得
所以x+y=6,x-y=20.
将它们组成新方程组,即
解得
例10:解方程组:
解:②-①,得x+y=1.③
由③得y=1-x.④
将④代入②,得2
020x+2
021(1-x)=2022,解得x=-1.
①
②
将x=-1代入④,得y=1-(-1)=2.
所以原方程组的解为
例11:解方程组:
解:①+②,得10
000x-10
000y=50
000,即x-y=5.③
①-②,得6
718x+6
718y=6
718,即x+y=1.④
③+④,得2x=6,解得x=3;
③-④,得-2y=4,解得y=-2.
①
②
所以原方程组的解为
拓展题(2)
1.若
,
则x+2y=
______
2.已知2ayb3x+1与-3ax-2b2-2y是同类项,则x
=
,y=__
_
-3
1
-1
3、若
,
则x,y的值为(
)
x=1,y=1
家庭作业
请完成课后相关练习。
