江苏省南通市通州区通海中学八年级数学下册 19.2.1 正比例函数课件(共23张PPT)
文档属性
| 名称 | 江苏省南通市通州区通海中学八年级数学下册 19.2.1 正比例函数课件(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-27 00:00:00 | ||
图片预览






文档简介
(共23张PPT)
19.2
一次函数
19.2.1
正比例函数
学习目标
1.理解正比例函数的概念.掌握正比例函数解析式特点,并能准确判断正比例函数。
2.会画正比例函数的图像,能说出正比例函数图像的特征并归纳正比例函数的性质。
问题1
2011年开始运营的京沪高速铁路全长1318千米设列车的平均速度为300千米每小时。考虑以下问题:
(1)京沪高铁的行程ykm与时间th之间有何数量关系?
情景导入
(1)京沪高铁列车的行程y(单位:km)与运行时间t(单位:h)之间有何数量关系?
y=300t(0≤t≤4.4)
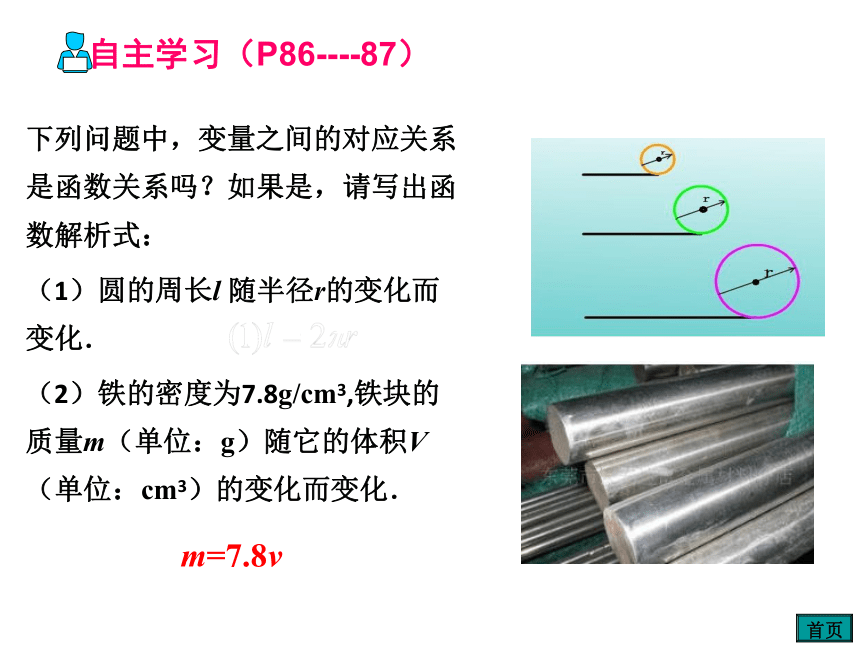
下列问题中,变量之间的对应关系是函数关系吗?如果是,请写出函数解析式:
(1)圆的周长l
随半径r的变化而变化.
(2)铁的密度为7.8g/cm3,铁块的质量m(单位:g)随它的体积V(单位:cm3)的变化而变化.
m=7.8v
自主学习(P86----87)
(3)每个练习本的厚度为0.5cm,
一些练习本摞在一起的总厚度h
(单位:cm)随练习本的本数n的
变化而变化.
(4)冷冻一个0°C的物体,使它每
分钟下降2°C,物体问题T(单位:°C)
随冷冻时间t(单位:min)的变化而变
化.
(3)h=0.5n
(4)T=-2t
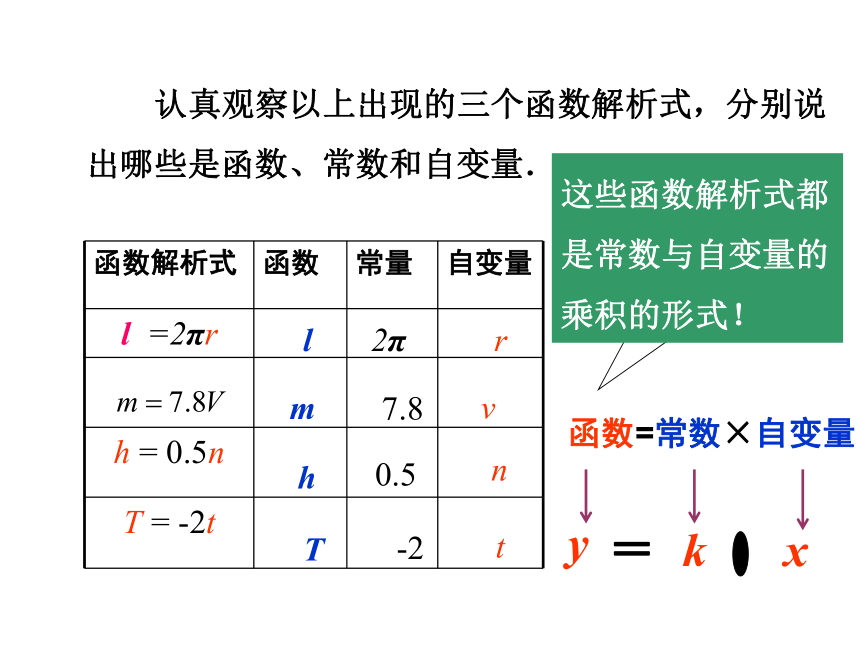
认真观察以上出现的三个函数解析式,分别说出哪些是函数、常数和自变量.
函数解析式
函数
常量
自变量
l
=2πr
h
=
0.5n
T
=
-2t
这些函数解析式有什么共同点?
这些函数解析式都是常数与自变量的乘积的形式!
2π
r
l
h
T
t
0.5
-2
n
函数=常数×自变量
y
k
x
=
m
v
7.8
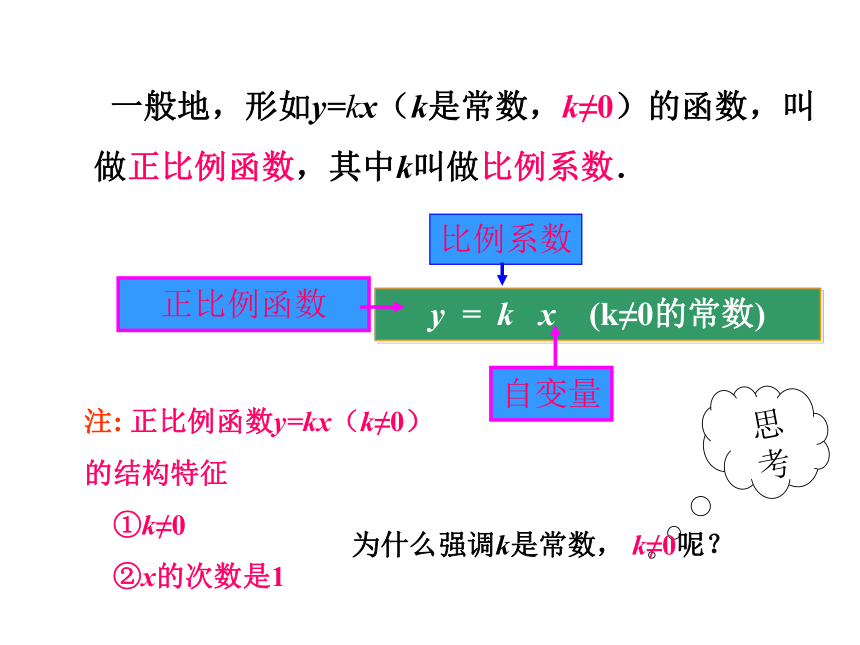
一般地,形如y=kx(k是常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数.
思考
为什么强调k是常数,
k≠0呢?
y
=
k
x
(k≠0的常数)
比例系数
自变量
正比例函数
注:
正比例函数y=kx(k≠0)
的结构特征
①k≠0
②x的次数是1
(1)y=-0.1x
(2)
(3)y=2x2
是正比例函数,
正比例系数为-0.1
是正比例函数,
正比例系数为0.5
不是正比例函数
判定一个函数是否是正比例函数,要从化简后来判断!
例1
判断下列函数解析式是否是正比例函数?如果是,指出其比例系数是多少?
(4)y2=4x
(5)y=-4x+3
(6)y=2(x-x2
)+2x2
不是正比例函数
不是正比例函数
是正比例函数,化简后为y=2x,正比例系数为2.
判定一个函数是否是正比例函数,要从化简后来判断!
例1
判断下列函数解析式是否是正比例函数?如果是,指出其比例系数是多少?
例2(1)如果y=(k-1)x,是y关于x的正比例函数,则k满足________________.
(2)如果y=kxk-1,是y关于x的正比例函数,则k=__________.
(3)如果y=3x+k-4,是y关于x的正比例函数,则k=_________.
k≠1
2
4
(4)若
是关于x的正比例函数,m=
.
-2
例题3.若y关于x-2成正比例函数,当x=3时,y=-4.试求出y与x的函数关系式.
1.列表;
2.描点;
3.连线.
画图步骤:
合作探究
活动:探究正比例函数的图象和性质
y
=2x
6
4
2
-2
-5
5
x
y
O
y
=2x
y
=x
y
=4x
6
4
2
-2
-5
5
x
y
O
在k>0
的情况下,图象是左低右高还是左高右低?
思考 对一般正比例函数y
=kx,当k>0时,它的图象形状是什么?位置怎样?
对应地,当自变量的值增大时,对应的函数值是随着增大还是减小?
y
=2x
y
=x
y
=4x
6
4
2
-2
-5
5
x
y
O
这些图象都是经过原点的
,函数y=2x的图象从左向右
,经过第
象限,y随x的增大而
;函数y=
的图象从左向右
,经过第
象限,y随x的增大而
.
直线
上升
一、三
增大
y=
上升
一、三
增大
说一说
根据前面的方法,请你画出
y=-1.5x
,
y=-4x的图象.
y=-4x
y=-1.5x
和你画的一样吗?
当k<0
时,正比例函数的图象特征及性质又怎样呢?
y
x
O
y=kx
(k是常数,k≠0)的图象是一条经过原点的直线
y=kx
经过的象限
从左向右
y随x的增大而
k>0
第一、三象限
上升
增大
k<0
第二、四象限
下降
减小
由于两点确定一条直线,画正比例函数图象时我们只需描点(0,0)和点
(1,k),连线即可.
两点
作图法
知识要点
O
例
3
用你认为最简单的方法画出下列函数的图象:
(1)
y=-3x;(2)
x
0
1
y=-3x
0
-3
0
y=-3x
例4
若正比例函数y=(k-3)x满足下列条件,求出k的范围.
(1)y
随x的增大而增大;
(2)图象经过一、三象限;
(3)图象如图所示.
k>3
k>3
k<3
O
x
y
例5.
比较大小:
(1)k1
k2;(2)k3
k4;
(3)比较k1,
k2,
k3,
k4大小,并用不等号连接.
<
k1<k2
<k3
<k4
4
2
-2
-4
4
x
y
O
y
=k4
x
-4
-2
2
y
=k3
x
y
=k2
x
y
=k1
x
<
课堂小结
一般地,形如y=kx(k是常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数.
y=kx
(k是常数,k≠0)的图象是一条经过原点的直线
y=kx
经过的象限
从左向右
y随x的增大而
k>0
第一、三象限
上升
增大
k<0
第二、四象限
下降
减小
19.2
一次函数
19.2.1
正比例函数
学习目标
1.理解正比例函数的概念.掌握正比例函数解析式特点,并能准确判断正比例函数。
2.会画正比例函数的图像,能说出正比例函数图像的特征并归纳正比例函数的性质。
问题1
2011年开始运营的京沪高速铁路全长1318千米设列车的平均速度为300千米每小时。考虑以下问题:
(1)京沪高铁的行程ykm与时间th之间有何数量关系?
情景导入
(1)京沪高铁列车的行程y(单位:km)与运行时间t(单位:h)之间有何数量关系?
y=300t(0≤t≤4.4)
下列问题中,变量之间的对应关系是函数关系吗?如果是,请写出函数解析式:
(1)圆的周长l
随半径r的变化而变化.
(2)铁的密度为7.8g/cm3,铁块的质量m(单位:g)随它的体积V(单位:cm3)的变化而变化.
m=7.8v
自主学习(P86----87)
(3)每个练习本的厚度为0.5cm,
一些练习本摞在一起的总厚度h
(单位:cm)随练习本的本数n的
变化而变化.
(4)冷冻一个0°C的物体,使它每
分钟下降2°C,物体问题T(单位:°C)
随冷冻时间t(单位:min)的变化而变
化.
(3)h=0.5n
(4)T=-2t
认真观察以上出现的三个函数解析式,分别说出哪些是函数、常数和自变量.
函数解析式
函数
常量
自变量
l
=2πr
h
=
0.5n
T
=
-2t
这些函数解析式有什么共同点?
这些函数解析式都是常数与自变量的乘积的形式!
2π
r
l
h
T
t
0.5
-2
n
函数=常数×自变量
y
k
x
=
m
v
7.8
一般地,形如y=kx(k是常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数.
思考
为什么强调k是常数,
k≠0呢?
y
=
k
x
(k≠0的常数)
比例系数
自变量
正比例函数
注:
正比例函数y=kx(k≠0)
的结构特征
①k≠0
②x的次数是1
(1)y=-0.1x
(2)
(3)y=2x2
是正比例函数,
正比例系数为-0.1
是正比例函数,
正比例系数为0.5
不是正比例函数
判定一个函数是否是正比例函数,要从化简后来判断!
例1
判断下列函数解析式是否是正比例函数?如果是,指出其比例系数是多少?
(4)y2=4x
(5)y=-4x+3
(6)y=2(x-x2
)+2x2
不是正比例函数
不是正比例函数
是正比例函数,化简后为y=2x,正比例系数为2.
判定一个函数是否是正比例函数,要从化简后来判断!
例1
判断下列函数解析式是否是正比例函数?如果是,指出其比例系数是多少?
例2(1)如果y=(k-1)x,是y关于x的正比例函数,则k满足________________.
(2)如果y=kxk-1,是y关于x的正比例函数,则k=__________.
(3)如果y=3x+k-4,是y关于x的正比例函数,则k=_________.
k≠1
2
4
(4)若
是关于x的正比例函数,m=
.
-2
例题3.若y关于x-2成正比例函数,当x=3时,y=-4.试求出y与x的函数关系式.
1.列表;
2.描点;
3.连线.
画图步骤:
合作探究
活动:探究正比例函数的图象和性质
y
=2x
6
4
2
-2
-5
5
x
y
O
y
=2x
y
=x
y
=4x
6
4
2
-2
-5
5
x
y
O
在k>0
的情况下,图象是左低右高还是左高右低?
思考 对一般正比例函数y
=kx,当k>0时,它的图象形状是什么?位置怎样?
对应地,当自变量的值增大时,对应的函数值是随着增大还是减小?
y
=2x
y
=x
y
=4x
6
4
2
-2
-5
5
x
y
O
这些图象都是经过原点的
,函数y=2x的图象从左向右
,经过第
象限,y随x的增大而
;函数y=
的图象从左向右
,经过第
象限,y随x的增大而
.
直线
上升
一、三
增大
y=
上升
一、三
增大
说一说
根据前面的方法,请你画出
y=-1.5x
,
y=-4x的图象.
y=-4x
y=-1.5x
和你画的一样吗?
当k<0
时,正比例函数的图象特征及性质又怎样呢?
y
x
O
y=kx
(k是常数,k≠0)的图象是一条经过原点的直线
y=kx
经过的象限
从左向右
y随x的增大而
k>0
第一、三象限
上升
增大
k<0
第二、四象限
下降
减小
由于两点确定一条直线,画正比例函数图象时我们只需描点(0,0)和点
(1,k),连线即可.
两点
作图法
知识要点
O
例
3
用你认为最简单的方法画出下列函数的图象:
(1)
y=-3x;(2)
x
0
1
y=-3x
0
-3
0
y=-3x
例4
若正比例函数y=(k-3)x满足下列条件,求出k的范围.
(1)y
随x的增大而增大;
(2)图象经过一、三象限;
(3)图象如图所示.
k>3
k>3
k<3
O
x
y
例5.
比较大小:
(1)k1
k2;(2)k3
k4;
(3)比较k1,
k2,
k3,
k4大小,并用不等号连接.
<
k1<k2
<k3
<k4
4
2
-2
-4
4
x
y
O
y
=k4
x
-4
-2
2
y
=k3
x
y
=k2
x
y
=k1
x
<
课堂小结
一般地,形如y=kx(k是常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数.
y=kx
(k是常数,k≠0)的图象是一条经过原点的直线
y=kx
经过的象限
从左向右
y随x的增大而
k>0
第一、三象限
上升
增大
k<0
第二、四象限
下降
减小
