2020年人教版数学六年级下册总复习《图形与几何》复习精选题(一)(含答案)
文档属性
| 名称 | 2020年人教版数学六年级下册总复习《图形与几何》复习精选题(一)(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 299.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-26 15:25:50 | ||
图片预览

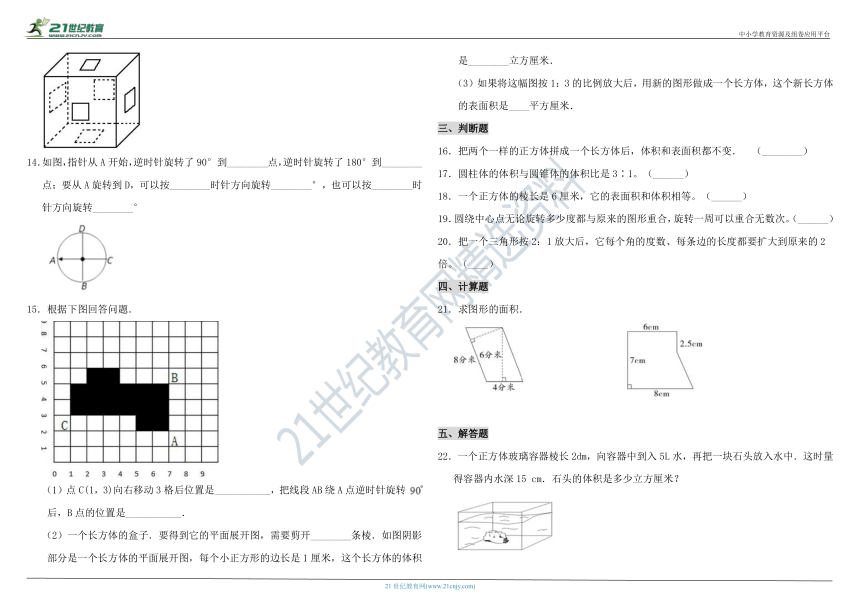
文档简介
中小学教育资源及组卷应用平台
2020年人教版数学
六年级下册总复习《图形与几何》复习精选题(一)
一、选择题
1.在的上方画
,在的下面画
,在的左边画
,在的右边画
.下面正确的是(??????
).
A.
B.????
C.
2.从由8个棱长是1厘米的小正方体拼成的大正方体中,拿走一个小正方体,如图,这时
它的表面积是(
)平方厘米.
A.18
B.21
C.24
3.有一个棱长是4厘米的正方体,从它的一个顶点处挖去一个棱长是1厘米的正方体后,
剩下物体表面积和原来的表面积相比较,(??
)
A.大了
B.小了
C.不变
D.无法确定
4.一个平行四边形的底是2.5厘米,高是底的1.2倍,这个平行四边形的面积是(
)
平方厘米。
A.3
B.7.5
C.3.85
5.一个长方形按3:1
放大后,得到的图形与原图形比较,正确的说法是(?
)
A.周长扩大9倍
B.周长缩小9倍
C.面积扩大9倍
D.面积缩小9倍
二、填空题
6.一根长1米的圆柱形木棒,锯成3段后,表面积增加了64平方分米,这根木棒的体积
是_____.
7.一个喷雾器的药箱容积是13L,如果每分钟喷出药液650ml,喷完一箱药液需要用
________分钟.
8.右图中小方格是正方形,若圆形的位置是(2,3),则三角形的位置是(________);
若三角形的面积为0.5cm2
,
则圆的面积为(________)cm2。(圆周率取3.14)
9.一根长2米的直圆柱木料,横着截去2分米,和原来比,剩下的圆柱体木料的表面积减
少12.56平方分米,原来圆柱体木料的底面积是______平方分米,体积是______立方分
米。
10.把60L水倒入棱长5dm的正方体容器里,水的高度是(______)分米.
11.一个长方体的底面积是32平方分米,高和宽都是4分米,这个长方体的表面积是______
平方分米。
12.一个长方体木块,长、宽、高分别是10厘米、6厘米和4厘米,把它加工成一个最大
的圆柱,这个圆柱的体积是_________立方厘米;如果这个圆柱的高是一个圆锥高的,
并且圆锥的底面积是圆柱底面积的25%,那么圆锥的体积是_________立方厘米.
13.在棱长为4cm的正方体的6个面上,各挖去一个棱长为1cm的正方体,挖后的正方体
的体积是________表面积是否增加了,若增加了,增加________
14.如图,指针从A开始,逆时针旋转了90°到________点,逆时针旋转了180°到________
点;要从A旋转到D,可以按________时针方向旋转________°,也可以按________时
针方向旋转________°
15.根据下图回答问题.
(1)点C(1,3)向右移动3格后位置是___________,把线段AB绕A点逆时针旋转
后,B点的位置是___________.
(2)一个长方体的盒子.要得到它的平面展开图,需要剪开________条棱.如图阴影
部分是一个长方体的平面展开图,每个小正方形的边长是1厘米,这个长方体的体积
是________立方厘米.
(3)如果将这幅图按1:3的比例放大后,用新的图形做成一个长方体,这个新长方体
的表面积是____平方厘米.
三、判断题
16.把两个一样的正方体拼成一个长方体后,体积和表面积都不变.
(________)
17.圆柱体的体积与圆锥体的体积比是3∶1。(______)
18.一个正方体的棱长是6厘米,它的表面积和体积相等。(______)
19.圆绕中心点无论旋转多少度都与原来的图形重合,旋转一周可以重合无数次。(______)
20.把一个三角形按2:1放大后,它每个角的度数、每条边的长度都要扩大到原来的2倍。(____)
四、计算题
21.求图形的面积.
五、解答题
22.一个正方体玻璃容器棱长2dm,向容器中到入5L水,再把一块石头放入水中.这时量
得容器内水深15
cm.石头的体积是多少立方厘米?
23.把1.2米长的长方体木料(如图),平均锯成3段,表面积比原来增加了2.4平方分
米,原来这根木料的体积是多少立方分米?
24.用铁皮制作圆柱形通风管,每节长60cm,底面半径5cm,制作10节这样的通风管,至
少需要多大面积的铁皮?
25.由于生产的需要,打算将一个半径为5cm的钢球重新铸造成一批半径为1cm的小钢球,
求这些小钢球的个数。
26.求影阴部分的面积.(单位:厘米)
27.工人叔叔在粉刷教室,教室的长是9m,宽是8m,高是3.6m,门窗面积为21m?,要粉
刷四周墙壁和顶棚。如果粉刷每平方米用环保漆300g,粉刷完这间教室共用环保漆多
少千克?
28.一个直角三角形ABC的两条直角边长分别是6cm和9cm,把它按4:1放大后得到三角
形DEF。三角形ABC与三角形的周长之比是多少?面积之比是多少?
六、作图题
29.根据下面说法,在下图中标出各场所的位置.
(1)书店在中心广场的东偏南45度的方向上,距离是2km.
(2)学校在中心广场的北偏西60度的方向上,距离是1.5km.
(3)肯得鸡在中心广场的正北方向上,距离是2.5km.
30.(1)把图中的长方形绕A点顺时针旋转90°,画出旋转后的图形.
(2)按1:2的比画出三角形缩小后的图形,缩小后的三角形的面积是原来的(
).
(3)如果一个小方格表示1平方厘米,在方格纸上设计一个面积是10平方厘米的轴对
称图形,并画出对称轴.
参考答案
1.B
2.C
3.C
4.B
5.C
6.160立方分米
7.20
8.3,1;0.785
9.3.14
62.8
10.2.4
11.160
12.125.6
47.1
13.
14.
B
C
顺
90
逆
270
15.(1)4;3;4;2
(2)7;4
(3)144
16.×
17.×
18.×
19.√
20.错误
21.24平方分米
46.5平方厘米
22.1000立方厘米
23.12立方分米
24.18840平方厘米
25.125个
26.(1)1.14平方厘米(2)15.44平方厘米(3)37.68平方厘米
27.52.02kg
28.周长之比是1:4,面积之比是1:16
29.解:
2千米=200000厘米,
书店的图上距离为:200000×
=4厘米,
1.5千米=150000厘米,
学校的图上距离为:150000×
=3厘米,
2.5千米=250000厘米,
肯德基的图上距离为:250000×
=5厘米,
由上述计算结果,在平面图中画出方向标,即可表示出书店、学校、肯德基的位置如下图所示:
30.(1)
(2)如图,﹙2×1.5÷2﹚÷﹙4×3÷2﹚=
(3)如图,答案不唯一.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
2020年人教版数学
六年级下册总复习《图形与几何》复习精选题(一)
一、选择题
1.在的上方画
,在的下面画
,在的左边画
,在的右边画
.下面正确的是(??????
).
A.
B.????
C.
2.从由8个棱长是1厘米的小正方体拼成的大正方体中,拿走一个小正方体,如图,这时
它的表面积是(
)平方厘米.
A.18
B.21
C.24
3.有一个棱长是4厘米的正方体,从它的一个顶点处挖去一个棱长是1厘米的正方体后,
剩下物体表面积和原来的表面积相比较,(??
)
A.大了
B.小了
C.不变
D.无法确定
4.一个平行四边形的底是2.5厘米,高是底的1.2倍,这个平行四边形的面积是(
)
平方厘米。
A.3
B.7.5
C.3.85
5.一个长方形按3:1
放大后,得到的图形与原图形比较,正确的说法是(?
)
A.周长扩大9倍
B.周长缩小9倍
C.面积扩大9倍
D.面积缩小9倍
二、填空题
6.一根长1米的圆柱形木棒,锯成3段后,表面积增加了64平方分米,这根木棒的体积
是_____.
7.一个喷雾器的药箱容积是13L,如果每分钟喷出药液650ml,喷完一箱药液需要用
________分钟.
8.右图中小方格是正方形,若圆形的位置是(2,3),则三角形的位置是(________);
若三角形的面积为0.5cm2
,
则圆的面积为(________)cm2。(圆周率取3.14)
9.一根长2米的直圆柱木料,横着截去2分米,和原来比,剩下的圆柱体木料的表面积减
少12.56平方分米,原来圆柱体木料的底面积是______平方分米,体积是______立方分
米。
10.把60L水倒入棱长5dm的正方体容器里,水的高度是(______)分米.
11.一个长方体的底面积是32平方分米,高和宽都是4分米,这个长方体的表面积是______
平方分米。
12.一个长方体木块,长、宽、高分别是10厘米、6厘米和4厘米,把它加工成一个最大
的圆柱,这个圆柱的体积是_________立方厘米;如果这个圆柱的高是一个圆锥高的,
并且圆锥的底面积是圆柱底面积的25%,那么圆锥的体积是_________立方厘米.
13.在棱长为4cm的正方体的6个面上,各挖去一个棱长为1cm的正方体,挖后的正方体
的体积是________表面积是否增加了,若增加了,增加________
14.如图,指针从A开始,逆时针旋转了90°到________点,逆时针旋转了180°到________
点;要从A旋转到D,可以按________时针方向旋转________°,也可以按________时
针方向旋转________°
15.根据下图回答问题.
(1)点C(1,3)向右移动3格后位置是___________,把线段AB绕A点逆时针旋转
后,B点的位置是___________.
(2)一个长方体的盒子.要得到它的平面展开图,需要剪开________条棱.如图阴影
部分是一个长方体的平面展开图,每个小正方形的边长是1厘米,这个长方体的体积
是________立方厘米.
(3)如果将这幅图按1:3的比例放大后,用新的图形做成一个长方体,这个新长方体
的表面积是____平方厘米.
三、判断题
16.把两个一样的正方体拼成一个长方体后,体积和表面积都不变.
(________)
17.圆柱体的体积与圆锥体的体积比是3∶1。(______)
18.一个正方体的棱长是6厘米,它的表面积和体积相等。(______)
19.圆绕中心点无论旋转多少度都与原来的图形重合,旋转一周可以重合无数次。(______)
20.把一个三角形按2:1放大后,它每个角的度数、每条边的长度都要扩大到原来的2倍。(____)
四、计算题
21.求图形的面积.
五、解答题
22.一个正方体玻璃容器棱长2dm,向容器中到入5L水,再把一块石头放入水中.这时量
得容器内水深15
cm.石头的体积是多少立方厘米?
23.把1.2米长的长方体木料(如图),平均锯成3段,表面积比原来增加了2.4平方分
米,原来这根木料的体积是多少立方分米?
24.用铁皮制作圆柱形通风管,每节长60cm,底面半径5cm,制作10节这样的通风管,至
少需要多大面积的铁皮?
25.由于生产的需要,打算将一个半径为5cm的钢球重新铸造成一批半径为1cm的小钢球,
求这些小钢球的个数。
26.求影阴部分的面积.(单位:厘米)
27.工人叔叔在粉刷教室,教室的长是9m,宽是8m,高是3.6m,门窗面积为21m?,要粉
刷四周墙壁和顶棚。如果粉刷每平方米用环保漆300g,粉刷完这间教室共用环保漆多
少千克?
28.一个直角三角形ABC的两条直角边长分别是6cm和9cm,把它按4:1放大后得到三角
形DEF。三角形ABC与三角形的周长之比是多少?面积之比是多少?
六、作图题
29.根据下面说法,在下图中标出各场所的位置.
(1)书店在中心广场的东偏南45度的方向上,距离是2km.
(2)学校在中心广场的北偏西60度的方向上,距离是1.5km.
(3)肯得鸡在中心广场的正北方向上,距离是2.5km.
30.(1)把图中的长方形绕A点顺时针旋转90°,画出旋转后的图形.
(2)按1:2的比画出三角形缩小后的图形,缩小后的三角形的面积是原来的(
).
(3)如果一个小方格表示1平方厘米,在方格纸上设计一个面积是10平方厘米的轴对
称图形,并画出对称轴.
参考答案
1.B
2.C
3.C
4.B
5.C
6.160立方分米
7.20
8.3,1;0.785
9.3.14
62.8
10.2.4
11.160
12.125.6
47.1
13.
14.
B
C
顺
90
逆
270
15.(1)4;3;4;2
(2)7;4
(3)144
16.×
17.×
18.×
19.√
20.错误
21.24平方分米
46.5平方厘米
22.1000立方厘米
23.12立方分米
24.18840平方厘米
25.125个
26.(1)1.14平方厘米(2)15.44平方厘米(3)37.68平方厘米
27.52.02kg
28.周长之比是1:4,面积之比是1:16
29.解:
2千米=200000厘米,
书店的图上距离为:200000×
=4厘米,
1.5千米=150000厘米,
学校的图上距离为:150000×
=3厘米,
2.5千米=250000厘米,
肯德基的图上距离为:250000×
=5厘米,
由上述计算结果,在平面图中画出方向标,即可表示出书店、学校、肯德基的位置如下图所示:
30.(1)
(2)如图,﹙2×1.5÷2﹚÷﹙4×3÷2﹚=
(3)如图,答案不唯一.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
