北师大版七年级数学下册 第二章相交线与平行线 单元提升练习题 (无答案)
文档属性
| 名称 | 北师大版七年级数学下册 第二章相交线与平行线 单元提升练习题 (无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 86.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-26 16:17:56 | ||
图片预览


文档简介
北师大版七年级数学下册单元提升练习题
第二章相交线与平行线
(无答案)
一、选择题
1.在同一平面内两条直线的位置关系是( )
A.相交或垂直
B.垂直或平行
C.平行或相交
D.平行或相交或垂直
2.(2018·大武口区期中)已知∠A=25°,则∠A的补角等于( )
A.65°
B.75°
C.155°
D.165°
3.∠1与∠2是两直线被第三条直线所截形成的同旁内角,则∠1与∠2的关系为( )
A.∠1+∠2=180°
B.∠1+∠2=90°
C.∠1=∠2
D.不能确定
4.如图,有以下四个条件:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5.其中能判定AB∥CD的条件的个数有(
)
A.1
B.2
C.3
D.4
5.如图所示,AB∥CD,OD平分∠AOD,OF⊥OE,∠D=50°,则∠BOF为(
)
A.35°
B.30°
C.25°
D.20°
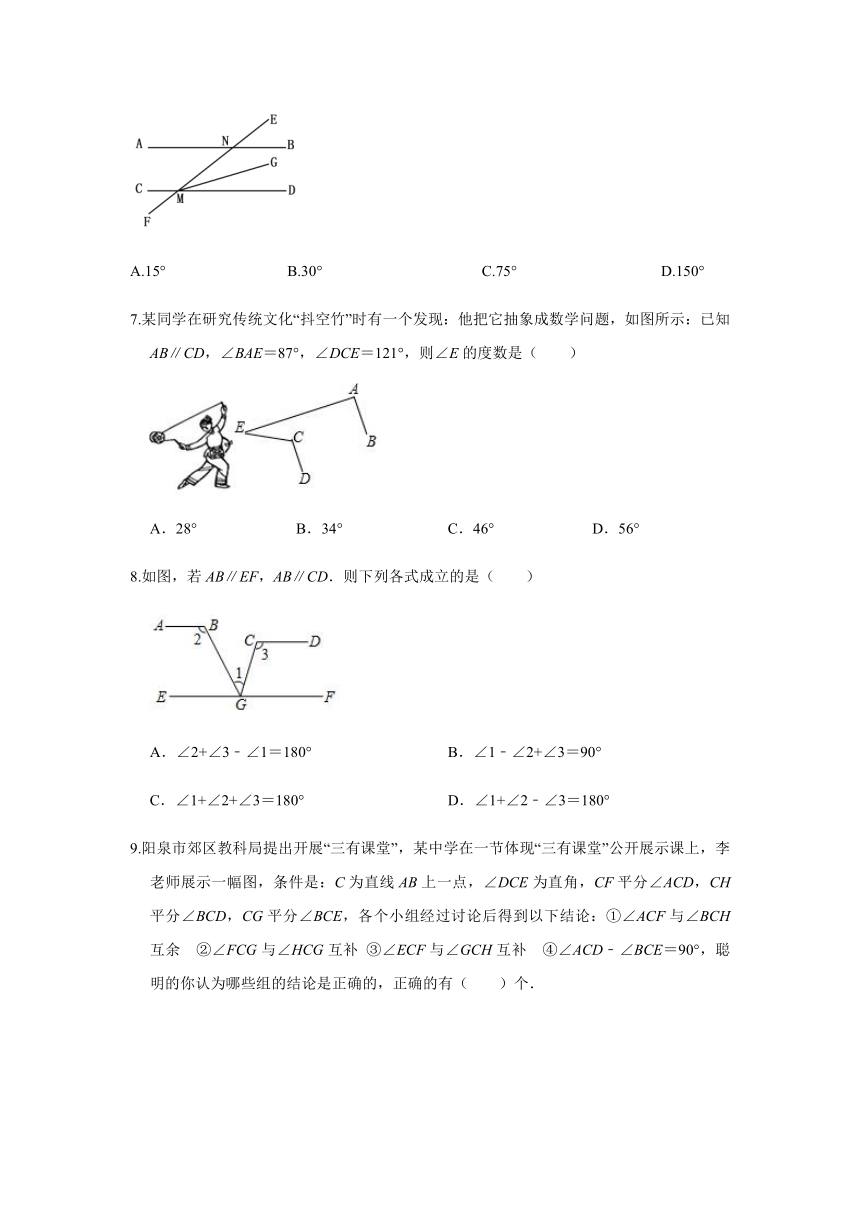
如图,已知直线AB∥CD,直线EF与AB、CD相交于N,M两点,MG平分∠EMD,若∠BNE=30°,则∠EMG等于(
)
A.15°
B.30°
C.75°
D.150°
7.某同学在研究传统文化“抖空竹”时有一个发现:他把它抽象成数学问题,如图所示:已知AB∥CD,∠BAE=87°,∠DCE=121°,则∠E的度数是( )
A.28°
B.34°
C.46°
D.56°
8.如图,若AB∥EF,AB∥CD.则下列各式成立的是( )
A.∠2+∠3﹣∠1=180°
B.∠1﹣∠2+∠3=90°
C.∠1+∠2+∠3=180°
D.∠1+∠2﹣∠3=180°
9.阳泉市郊区教科局提出开展“三有课堂”,某中学在一节体现“三有课堂”公开展示课上,李老师展示一幅图,条件是:C为直线AB上一点,∠DCE为直角,CF平分∠ACD,CH平分∠BCD,CG平分∠BCE,各个小组经过讨论后得到以下结论:①∠ACF与∠BCH互余
②∠FCG与∠HCG互补
③∠ECF与∠GCH互补
④∠ACD﹣∠BCE=90°,聪明的你认为哪些组的结论是正确的,正确的有( )个.
A.1
B.2
C.3
D.4
二、填空题
10.如图,当剪刀口∠AOB增大21°时,∠COD增大
度.
11.如图,是李晓松同学在运动会跳远比赛中最好的一跳,甲、乙、丙三名同学分别测得PA=5.52米,PB=5.37米,MA=5.60米,那么他的跳远成绩应该为
米.
12.已知一个角的补角比这个角的余角的3倍大20°,则这个角的度数为
.
13.如图,直线a和直线b被直线c所截,给出下列条件:
①∠1=∠2;
②∠3=∠6;
③∠4+∠7=180°;④∠5=∠8.
其中不能判断a∥b的条件的序号是
.
14.如图,已知BE平分∠ABC,且BE∥DC,若∠ABC=50°,则∠C的度数是
.
15.如图,点A,B,C,D在同一直线上,BF平分∠EBD,CG∥BF,若∠EBA=α°,则∠GCD=
°(用关于α的代数式表示)
解答题
16.补全下列推理过程:
如图,已知AB∥CE,∠A=∠E,试说明:∠CGD=∠FHB.
解:因为AB∥CE(
),
所以∠A=∠
(
).
因为∠A=∠E(已知),
所以∠
=∠
(
).
所以
∥
(
).
所以∠CGD=∠
(
).
因为∠FHB=∠GHE(
),
所以∠CGD=∠FHB(
).
17.已知:如图,∠1=∠2,∠3=100°,∠B=80°.求证:EF∥CD.
18.如图,已知AB∥CD,∠B=60°,CM平分∠BCE,∠MCN=90°,求∠DCN的度数.
19.如图,把一个长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置,若∠EFB=65°,求∠AED′的度数.
20.如图,在△ABC
中,CD⊥AB,垂足为
D,点
E
在
BC
上
EF⊥AB,垂足为
F.
(1)CD
与
EF
平行吗?为什么?
(2)如果∠1=∠2,试判断
DG
与
BC
的位置关系,并说明理由.
21.如图,已知AB∥CD,∠ABE的平分线与∠CDE的平分线相交于点F.
(1)在图1中,求证:
①∠ABE+∠CDE+∠E=360°;
②∠ABF+∠CDF=∠BFD;
(2)如图2,当∠ABM=∠ABF,∠CDM=∠CDF时,请你写出∠M与∠E之间的关系,并加以证明;
(3)当∠ABM=∠ABF,∠CDM=∠CDF,且∠E=m°时,请你直接写出∠M的度数(用含m,n的式子表示)
第二章相交线与平行线
(无答案)
一、选择题
1.在同一平面内两条直线的位置关系是( )
A.相交或垂直
B.垂直或平行
C.平行或相交
D.平行或相交或垂直
2.(2018·大武口区期中)已知∠A=25°,则∠A的补角等于( )
A.65°
B.75°
C.155°
D.165°
3.∠1与∠2是两直线被第三条直线所截形成的同旁内角,则∠1与∠2的关系为( )
A.∠1+∠2=180°
B.∠1+∠2=90°
C.∠1=∠2
D.不能确定
4.如图,有以下四个条件:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5.其中能判定AB∥CD的条件的个数有(
)
A.1
B.2
C.3
D.4
5.如图所示,AB∥CD,OD平分∠AOD,OF⊥OE,∠D=50°,则∠BOF为(
)
A.35°
B.30°
C.25°
D.20°
如图,已知直线AB∥CD,直线EF与AB、CD相交于N,M两点,MG平分∠EMD,若∠BNE=30°,则∠EMG等于(
)
A.15°
B.30°
C.75°
D.150°
7.某同学在研究传统文化“抖空竹”时有一个发现:他把它抽象成数学问题,如图所示:已知AB∥CD,∠BAE=87°,∠DCE=121°,则∠E的度数是( )
A.28°
B.34°
C.46°
D.56°
8.如图,若AB∥EF,AB∥CD.则下列各式成立的是( )
A.∠2+∠3﹣∠1=180°
B.∠1﹣∠2+∠3=90°
C.∠1+∠2+∠3=180°
D.∠1+∠2﹣∠3=180°
9.阳泉市郊区教科局提出开展“三有课堂”,某中学在一节体现“三有课堂”公开展示课上,李老师展示一幅图,条件是:C为直线AB上一点,∠DCE为直角,CF平分∠ACD,CH平分∠BCD,CG平分∠BCE,各个小组经过讨论后得到以下结论:①∠ACF与∠BCH互余
②∠FCG与∠HCG互补
③∠ECF与∠GCH互补
④∠ACD﹣∠BCE=90°,聪明的你认为哪些组的结论是正确的,正确的有( )个.
A.1
B.2
C.3
D.4
二、填空题
10.如图,当剪刀口∠AOB增大21°时,∠COD增大
度.
11.如图,是李晓松同学在运动会跳远比赛中最好的一跳,甲、乙、丙三名同学分别测得PA=5.52米,PB=5.37米,MA=5.60米,那么他的跳远成绩应该为
米.
12.已知一个角的补角比这个角的余角的3倍大20°,则这个角的度数为
.
13.如图,直线a和直线b被直线c所截,给出下列条件:
①∠1=∠2;
②∠3=∠6;
③∠4+∠7=180°;④∠5=∠8.
其中不能判断a∥b的条件的序号是
.
14.如图,已知BE平分∠ABC,且BE∥DC,若∠ABC=50°,则∠C的度数是
.
15.如图,点A,B,C,D在同一直线上,BF平分∠EBD,CG∥BF,若∠EBA=α°,则∠GCD=
°(用关于α的代数式表示)
解答题
16.补全下列推理过程:
如图,已知AB∥CE,∠A=∠E,试说明:∠CGD=∠FHB.
解:因为AB∥CE(
),
所以∠A=∠
(
).
因为∠A=∠E(已知),
所以∠
=∠
(
).
所以
∥
(
).
所以∠CGD=∠
(
).
因为∠FHB=∠GHE(
),
所以∠CGD=∠FHB(
).
17.已知:如图,∠1=∠2,∠3=100°,∠B=80°.求证:EF∥CD.
18.如图,已知AB∥CD,∠B=60°,CM平分∠BCE,∠MCN=90°,求∠DCN的度数.
19.如图,把一个长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置,若∠EFB=65°,求∠AED′的度数.
20.如图,在△ABC
中,CD⊥AB,垂足为
D,点
E
在
BC
上
EF⊥AB,垂足为
F.
(1)CD
与
EF
平行吗?为什么?
(2)如果∠1=∠2,试判断
DG
与
BC
的位置关系,并说明理由.
21.如图,已知AB∥CD,∠ABE的平分线与∠CDE的平分线相交于点F.
(1)在图1中,求证:
①∠ABE+∠CDE+∠E=360°;
②∠ABF+∠CDF=∠BFD;
(2)如图2,当∠ABM=∠ABF,∠CDM=∠CDF时,请你写出∠M与∠E之间的关系,并加以证明;
(3)当∠ABM=∠ABF,∠CDM=∠CDF,且∠E=m°时,请你直接写出∠M的度数(用含m,n的式子表示)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
