北师大版七年级数学下册第四章三角形-构造全等三角形的五种常用方法习题课件(16张ppt)
文档属性
| 名称 | 北师大版七年级数学下册第四章三角形-构造全等三角形的五种常用方法习题课件(16张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 227.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-27 19:20:38 | ||
图片预览





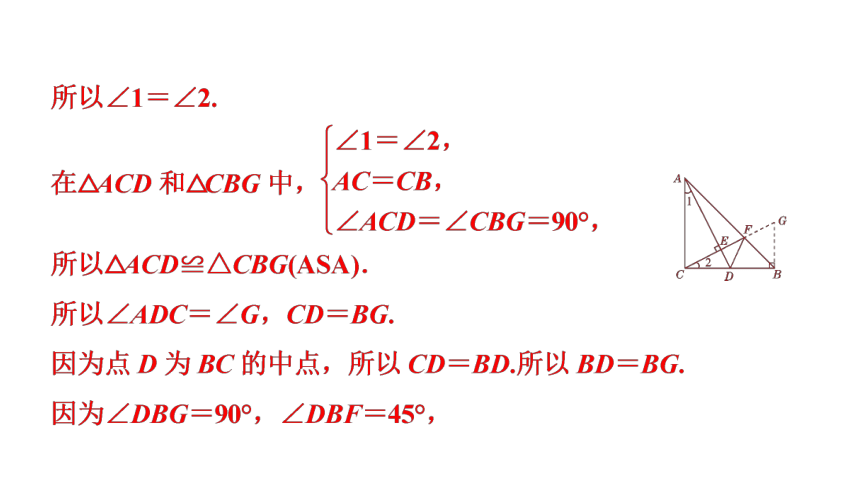
文档简介
(共16张PPT)
第四章
三角形
构造全等三角形的五种常用方法
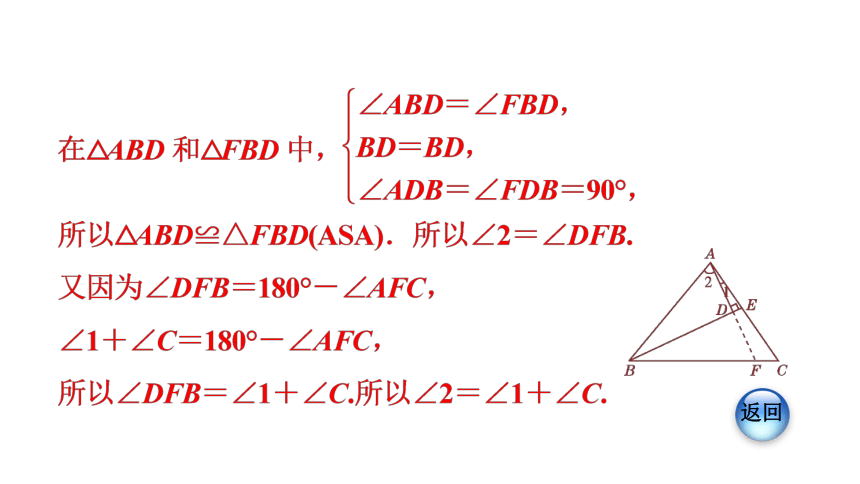
1.如图,在△ABC中,BE是∠ABC的平分线,AD⊥BE,垂足为D.试说明:∠2=∠1+∠C.
1
方
法
翻折法
解:如图,延长AD交BC于点F(相当于将AB边向下翻折,与BC边重合,A点落在F点处,折痕为BE).
?因为BE平分∠ABC,
所以∠ABE=∠CBE.
因为BD⊥AD,
所以∠ADB=∠FDB=90°.
返回
2.如图,在直角三角形ABC中,∠ACB=90°,AC=BC,∠ABC=45°,点D为BC的中点,CE⊥AD于点E,其延长线交AB于点F,连接DF.
试说明:∠ADC=∠BDF.
2
方
法
构造法
解:如图,过点B作BG⊥BC交CF的延长线于点G.
因为∠ACB=90°,所以∠2+∠ACF=90°.
因为CE⊥AD,
所以∠AEC=90°.
所以∠1+∠ACF=180°-∠AEC=180°-90°=90°.
因为CE⊥AD,所以∠AEC=90°.
所以∠1+∠ACF=180°-∠AEC=180°-90°=90°.
返回
3.如图,在正方形ABCD中,E为BC上的一点,F为CD上的一点,BE+DF=EF,求∠EAF的度数.
3
方
法
旋转法
解:如图,延长CB到点H,使得BH=DF,连接AH.
返回
4.如图,在△ABC中,D为BC的中点.若AB=5,AC=3,求AD长度的取值范围.
4
方
法
倍长中线法
解:如图,延长AD至点E,使DE=AD,连接BE.
因为D为BC的中点,所以CD=BD.
又因为AD=ED,∠ADC=∠EDB,
所以△ADC≌△EDB(SAS).所以AC=EB.
因为AB-EB所以AB-AC<2AD又因为AB=5,AC=3,
所以2<2AD<8.
所以1返回
5.如图,在正方形ABCD中,E是AB上一点,点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
5
方
法
截长补短法
解:成立.理由如下:
如图,延长AD至F,使DF=BE,连接CF.
在正方形ABCD中,BC=DC,∠B=∠CDA=90°,
所以∠CDF=∠B=90°.
又因为BE=DF,所以△CBE≌△CDF(SAS).
所以CE=CF,∠BCE=∠DCF.
所以∠BCE+∠ECD=∠DCF+∠ECD.所以∠ECF=∠BCD=90°.
因为∠GCE=45°,所以∠GCF=∠GCE=45°.
又因为CE=CF,GC=GC,
所以△ECG≌△FCG(SAS).所以GE=GF.
所以GE=DF+GD=BE+GD.
返回
第四章
三角形
构造全等三角形的五种常用方法
1.如图,在△ABC中,BE是∠ABC的平分线,AD⊥BE,垂足为D.试说明:∠2=∠1+∠C.
1
方
法
翻折法
解:如图,延长AD交BC于点F(相当于将AB边向下翻折,与BC边重合,A点落在F点处,折痕为BE).
?因为BE平分∠ABC,
所以∠ABE=∠CBE.
因为BD⊥AD,
所以∠ADB=∠FDB=90°.
返回
2.如图,在直角三角形ABC中,∠ACB=90°,AC=BC,∠ABC=45°,点D为BC的中点,CE⊥AD于点E,其延长线交AB于点F,连接DF.
试说明:∠ADC=∠BDF.
2
方
法
构造法
解:如图,过点B作BG⊥BC交CF的延长线于点G.
因为∠ACB=90°,所以∠2+∠ACF=90°.
因为CE⊥AD,
所以∠AEC=90°.
所以∠1+∠ACF=180°-∠AEC=180°-90°=90°.
因为CE⊥AD,所以∠AEC=90°.
所以∠1+∠ACF=180°-∠AEC=180°-90°=90°.
返回
3.如图,在正方形ABCD中,E为BC上的一点,F为CD上的一点,BE+DF=EF,求∠EAF的度数.
3
方
法
旋转法
解:如图,延长CB到点H,使得BH=DF,连接AH.
返回
4.如图,在△ABC中,D为BC的中点.若AB=5,AC=3,求AD长度的取值范围.
4
方
法
倍长中线法
解:如图,延长AD至点E,使DE=AD,连接BE.
因为D为BC的中点,所以CD=BD.
又因为AD=ED,∠ADC=∠EDB,
所以△ADC≌△EDB(SAS).所以AC=EB.
因为AB-EB
所以2<2AD<8.
所以1
5.如图,在正方形ABCD中,E是AB上一点,点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
5
方
法
截长补短法
解:成立.理由如下:
如图,延长AD至F,使DF=BE,连接CF.
在正方形ABCD中,BC=DC,∠B=∠CDA=90°,
所以∠CDF=∠B=90°.
又因为BE=DF,所以△CBE≌△CDF(SAS).
所以CE=CF,∠BCE=∠DCF.
所以∠BCE+∠ECD=∠DCF+∠ECD.所以∠ECF=∠BCD=90°.
因为∠GCE=45°,所以∠GCF=∠GCE=45°.
又因为CE=CF,GC=GC,
所以△ECG≌△FCG(SAS).所以GE=GF.
所以GE=DF+GD=BE+GD.
返回
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
