人教版七年级数学下册 5.1.2 垂线课件 (共15张PPT)
文档属性
| 名称 | 人教版七年级数学下册 5.1.2 垂线课件 (共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-27 00:00:00 | ||
图片预览





文档简介
(共15张PPT)
1.理解垂线的有关概念、性质及画法;(重点)
2.知道垂线段和点到直线的距离的概念,并会应用
其解决问题.
(重点、难点)
学习目标
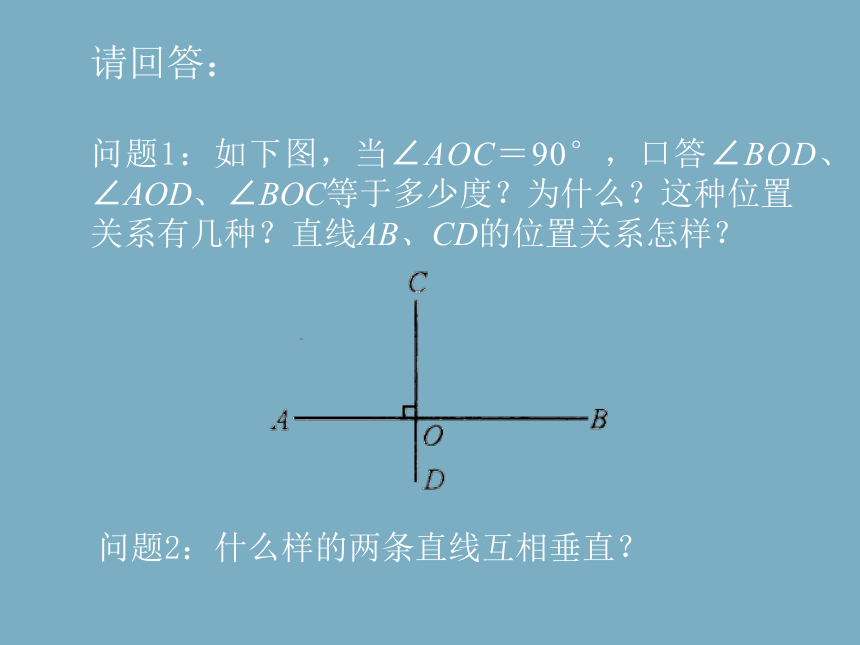
请回答:
问题2:什么样的两条直线互相垂直?
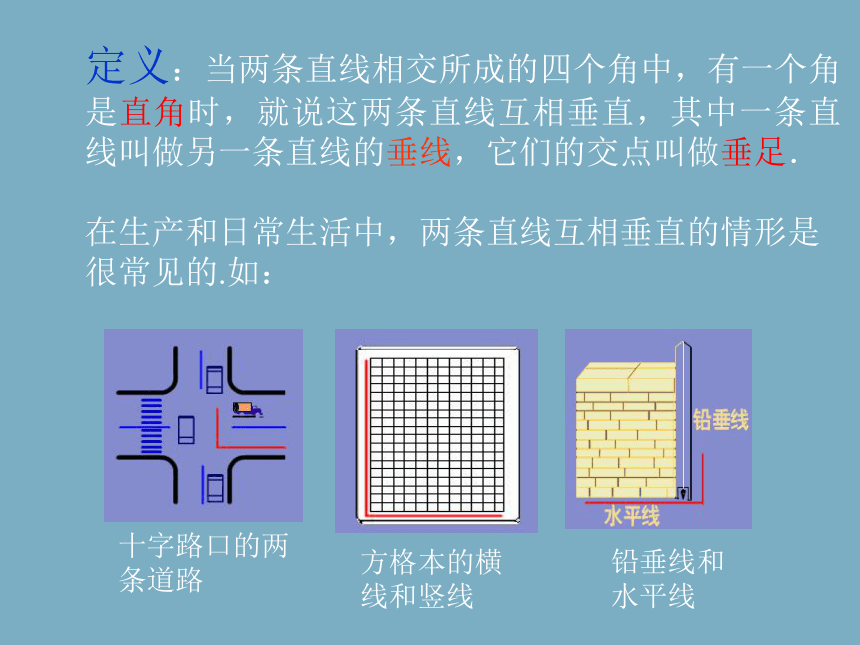
定义:当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,它们的交点叫做垂足.
在生产和日常生活中,两条直线互相垂直的情形是很常见的.如:
垂直的记法、读法
垂直的判定
∵∠AOC=90°(已知),
∴AB⊥CD(垂直的定义).
如果直线
AB、CD
相交于点O,∠AOC=90°(或三个角中的一个角等于90°),那么
AB⊥CD.
这个推理过程可以写成:
∵AB⊥CD(已知),
∴∠AOC=90°(垂直的定义).
如果AB⊥CD,那么所得的四个角中,必有一个是直角.这个推理过程可以写成:
垂线的性质1:过一点有且只有一条直线与已知直线垂直.
问题3:
(1)“过一点”包括几种情况?(两种)
(2)“有且只有”是什么意思?(唯一性)
垂线的性质
a
过P点可做直线
a
的垂线有几条(1条)
直线有几条?(无数条)那条最短?
1
(1)如图1,若直线m、n相交于点O,∠1=90°,则
;
(2)若直线AB、CD相交于点O,且AB⊥CD,则
∠BOD
=______;
(3)如图2,BO⊥AO,∠BOC与∠BOA的度数之比
为1∶5,那么∠COA=____,∠BOC的补角为
.
m⊥n
90°
72°
162°
例题
图1
图2
2.如图,下列说法正确的是(
)
A.线段AB叫做点B到直线AC的距离
B.线段AB的长度叫作点A到直线AC的距离
C.线段BD的长度叫作点D到直线BC的距离
D.线段BD的长度叫作点B到直线AC的距离
3.两条直线相交所成的四个角中,下列条件中能
判定两条直线垂直的是(
)
A.
有两个角相等
B.有两对角相等
C.
有三个角相等
D.有四对邻补角
4.如图,
AC⊥BC,
∠C=90°
,线段AC、BC、CD中最短的是
(
)
A.
AC
B.
BC
C.
CD
D.
不能确定
5.如图,直线AB、CD相交于点E,EF⊥AB于E,若∠CEF=58°,则∠BED的度数为
.
6.如图,AO⊥FD,OD为∠BOC的平分线,OE为射线OB的反向延长线,若∠AOB=40°,求∠EOF、∠COE的度数.
解:∵AO⊥OD且∠AOB=40°,
∴∠BOD=90°-40°=50°,
∴∠EOF=50°.
又∵OD平分∠BOC,
∴∠DOC=∠BOD=50°,
∴∠COE=180°-50°-50°=80°.
(1)
垂直的定义、画法及判定.
(2)
垂线的性质.
(3)点到直线的距离
1.理解垂线的有关概念、性质及画法;(重点)
2.知道垂线段和点到直线的距离的概念,并会应用
其解决问题.
(重点、难点)
学习目标
请回答:
问题2:什么样的两条直线互相垂直?
定义:当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,它们的交点叫做垂足.
在生产和日常生活中,两条直线互相垂直的情形是很常见的.如:
垂直的记法、读法
垂直的判定
∵∠AOC=90°(已知),
∴AB⊥CD(垂直的定义).
如果直线
AB、CD
相交于点O,∠AOC=90°(或三个角中的一个角等于90°),那么
AB⊥CD.
这个推理过程可以写成:
∵AB⊥CD(已知),
∴∠AOC=90°(垂直的定义).
如果AB⊥CD,那么所得的四个角中,必有一个是直角.这个推理过程可以写成:
垂线的性质1:过一点有且只有一条直线与已知直线垂直.
问题3:
(1)“过一点”包括几种情况?(两种)
(2)“有且只有”是什么意思?(唯一性)
垂线的性质
a
过P点可做直线
a
的垂线有几条(1条)
直线有几条?(无数条)那条最短?
1
(1)如图1,若直线m、n相交于点O,∠1=90°,则
;
(2)若直线AB、CD相交于点O,且AB⊥CD,则
∠BOD
=______;
(3)如图2,BO⊥AO,∠BOC与∠BOA的度数之比
为1∶5,那么∠COA=____,∠BOC的补角为
.
m⊥n
90°
72°
162°
例题
图1
图2
2.如图,下列说法正确的是(
)
A.线段AB叫做点B到直线AC的距离
B.线段AB的长度叫作点A到直线AC的距离
C.线段BD的长度叫作点D到直线BC的距离
D.线段BD的长度叫作点B到直线AC的距离
3.两条直线相交所成的四个角中,下列条件中能
判定两条直线垂直的是(
)
A.
有两个角相等
B.有两对角相等
C.
有三个角相等
D.有四对邻补角
4.如图,
AC⊥BC,
∠C=90°
,线段AC、BC、CD中最短的是
(
)
A.
AC
B.
BC
C.
CD
D.
不能确定
5.如图,直线AB、CD相交于点E,EF⊥AB于E,若∠CEF=58°,则∠BED的度数为
.
6.如图,AO⊥FD,OD为∠BOC的平分线,OE为射线OB的反向延长线,若∠AOB=40°,求∠EOF、∠COE的度数.
解:∵AO⊥OD且∠AOB=40°,
∴∠BOD=90°-40°=50°,
∴∠EOF=50°.
又∵OD平分∠BOC,
∴∠DOC=∠BOD=50°,
∴∠COE=180°-50°-50°=80°.
(1)
垂直的定义、画法及判定.
(2)
垂线的性质.
(3)点到直线的距离
