人教版高一物理必修2第7章 机械能守恒定律——复习学案word版含答案
文档属性
| 名称 | 人教版高一物理必修2第7章 机械能守恒定律——复习学案word版含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 105.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-05-26 18:05:12 | ||
图片预览




文档简介
必修二第七章
机械能守恒定律复习(一)
2019--2020学年第二学期第
号
备课组长签字
教研组长签字:
编写人:李俊杰
班级:
第
组
姓名:
知识点复习
一、功
1.做功的两个必要条件:力和物体在力的方向上发生的位移.
2.公式:W=
适用于恒力做功.其中α为F、l方向间夹角,l为物体对地的位移.
二、功率
1.定义:功与完成这些功所用时间的比值.
2.物理意义:描述力对物体做功的快慢.
3.公式:
(1)定义式:P=
,P为时间t内的平均功率.
(2)推论式:P=
.(α为F与v的夹角)
三、动能
1.定义:物体由于运动而具有的能.
2.表达式:Ek=
.
四、动能定理
1.内容:力在一个过程中对物体做的功,等于物体在这个过程中动能的变化.
2.表达式:W=Ek2-Ek1=
.
3.适用范围:
(1)动能定理既适用于直线运动,也适用于曲线运动.
(2)既适用于恒力做功,也适用于变力做功.
(3)力可以是各种性质的力,既可以同时作用,也可以不同时作用.
4.应用动能定理解题的基本思路:
(1)选取研究对象,明确它的运动过程;
(2)分析研究对象的受力情况和各力的做功情况:
(3)明确研究对象在过程的初末状态的动能Ek1和Ek2;
(4)列动能定理的方程W合=Ek2-Ek1及其他必要的解题方程,进行求解.
五、重力势能
1.定义:物体的重力势能等于它所受重力与高度的乘积.
2.公式:Ep=
.
3.特点:
(1)系统性:重力势能是地球和物体共有的.
(2)相对性:重力势能的大小与参考平面的选取有关.重力势能的变化是绝对的,与参考平面的选取无关.
5.重力做功与重力势能变化的关系:
重力做正功时,重力势能减小;
重力做负功时,重力势能增大;重力做多少正(负)功,重力势能就减小(增大)多少,即WG=
.
六、弹性势能
1.定义:物体由于发生弹性形变而具有的能.
2.大小:弹性势能的大小与形变量及劲度系数有关,弹簧的形变量越大,劲度系数越大,弹簧的弹性势能越大.
3.弹力做功与弹性势能变化的关系:弹力做正功,弹性势能减小;弹力做负功,弹性势能增大.
七、机械能守恒定律
1.内容:在只有重力或弹力做功的物体系统内,动能与势能可以相互转化,而总的机械能保持不变.
2.表达式:
(1)守恒观点:
(要选零势能参考平面).
(2)转化观点:
(不用选零势能参考平面).
(3)转移观点:
(不用选零势能参考平面).
3.机械能守恒的条件:只有重力(或弹力)做功或虽有其他外力做功但其他力做功的代数和为零.
4.应用机械能守恒定律解题的一般步骤:
(1)选取研究对象
(2)分析受力情况和各力做功情况,确定是否符合机械能守恒条件.
(3)确定初末状态的机械能或运动过程中物体机械能的转化情况.
(4)选择合适的表达式列出方程,进行求解.
(5)对计算结果进行必要的讨论和说明.
达标检测
一、选择题
1、一人乘电梯从1楼到30楼,在此过程中经历了先加速、后匀速、再减速的运动过程,则电梯支持力对人做功情况是( )
A.加速时做正功,匀速时不做功,减速时做负功
B.加速时做正功,匀速和减速时做负功
C.加速和匀速时做正功,减速时做负功
D.始终做正功
2、选择不同的水平面作为参考平面,物体在某一位置的重力势能和某一过程中重力势能的改变量( )
A.都具有不同的数值
B.都具有相同的数值
C.前者具有相同数值,后者具有不同数值
D.前者具有不同数值,后者具有相同数值
3、某同学在桌面上用一个小钢球和一个弹簧来探究弹簧的弹性势能。弹簧一端固定(如图所示),另一端用钢球压缩弹簧后释放,钢球被弹出后落地。他发现弹簧压缩得越多,钢球被弹出得越远,由此能得出的结论应是( )
A.弹性势能与形变量有关,形变量越大,弹性势能越大
B.弹性势能与形变量有关,形变量越大,弹性势能越小
C.弹性势能与劲度系数有关,劲度系数越大,弹性势能越大
D.弹性势能与劲度系数有关,劲度系数越大,弹性势能越小
4、一物体质量为1kg,速度为10m/s,它的动能是(?????
)
A.5J??????
B.10J??????
C.50J??????
D.100J
5、(双选)下列叙述中正确的是( )
A.做匀速直线运动的物体的机械能一定守恒
B.做变速直线运动的物体的机械能可能守恒
C.外力对物体做功为零,物体的机械能一定守恒
D.系统内只有重力和弹力做功时,系统的机械能一定守恒
6、(多选)质量为4kg,的物体被人由静止开始向上提升0.25m后速度达1m/s,则下列判断正确的是(
)
A.人对物体做功12J
B.合外力对物体做功2J
C.物体克服重力做功10J
D.人对物体做的功等于物体增加的动能
二、非选择题
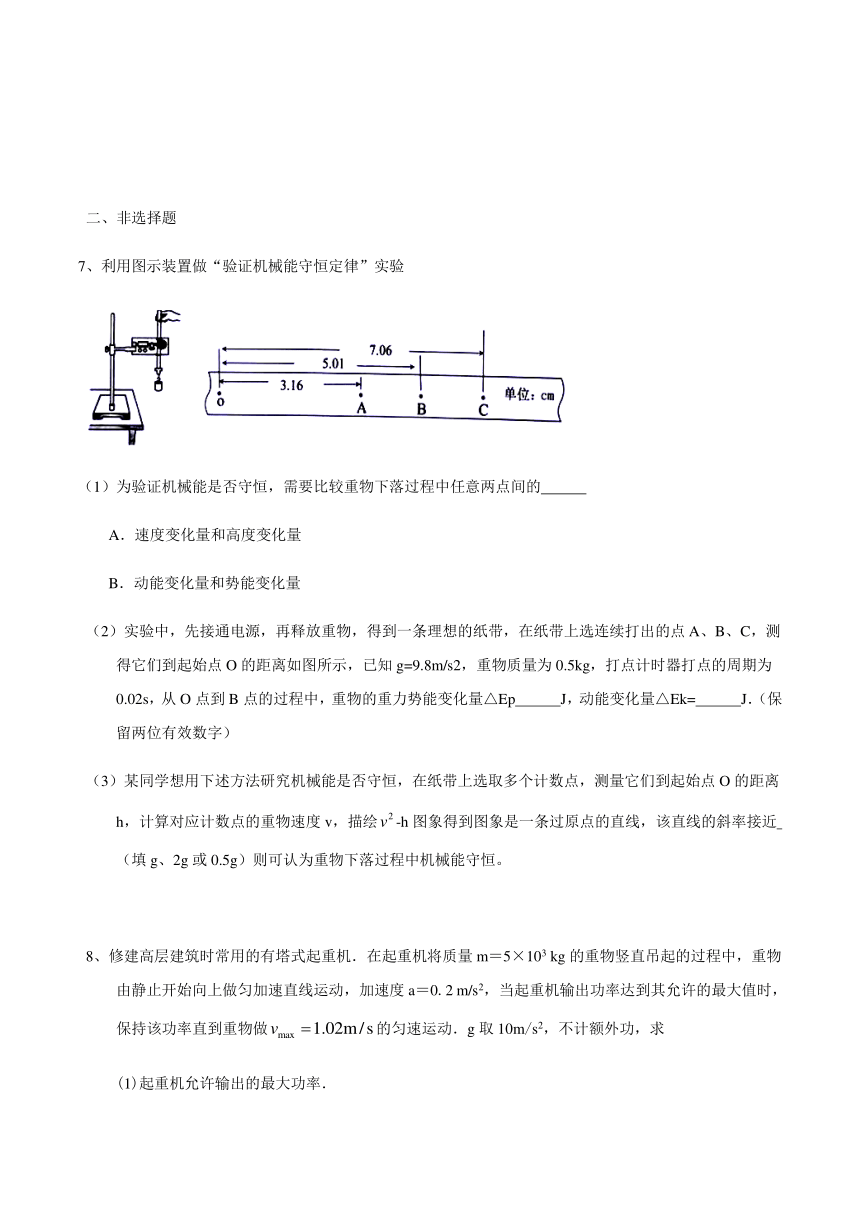
7、利用图示装置做“验证机械能守恒定律”实验
(1)为验证机械能是否守恒,需要比较重物下落过程中任意两点间的
A.速度变化量和高度变化量
B.动能变化量和势能变化量
(2)实验中,先接通电源,再释放重物,得到一条理想的纸带,在纸带上选连续打出的点A、B、C,测得它们到起始点O的距离如图所示,已知g=9.8m/s2,重物质量为0.5kg,打点计时器打点的周期为0.02s,从O点到B点的过程中,重物的重力势能变化量△Ep
J,动能变化量△Ek=
J.(保留两位有效数字)
(3)某同学想用下述方法研究机械能是否守恒,在纸带上选取多个计数点,测量它们到起始点O的距离h,计算对应计数点的重物速度v,描绘-h图象得到图象是一条过原点的直线,该直线的斜率接近
(填g、2g或0.5g)则可认为重物下落过程中机械能守恒。
8、修建高层建筑时常用的有塔式起重机.在起重机将质量m=5×103
kg的重物竖直吊起的过程中,重物由静止开始向上做匀加速直线运动,加速度a=0.2
m/s2,当起重机输出功率达到其允许的最大值时,保持该功率直到重物做的匀速运动.g取10m/s2,不计额外功,求
(1)起重机允许输出的最大功率.
(2)重物做匀加速直线运动所经历的时间和起重机在第2秒末的输出功率.
一、功
1.做功的两个必要条件:力和物体在力的方向上发生的位移.
2.公式:W=Flcos_α.适用于恒力做功.其中α为F、l方向间夹角,l为物体对地的位移.
二、功率
1.定义:功与完成这些功所用时间的比值.
2.物理意义:描述力对物体做功的快慢.
3.公式:
(1)定义式:P=,P为时间t内的平均功率.
(2)推论式:P=Fvcos_α.(α为F与v的夹角)
三、动能
1.定义:物体由于运动而具有的能.
2.表达式:Ek=mv2.
四、动能定理
1.内容:力在一个过程中对物体做的功,等于物体在这个过程中动能的变化.
2.表达式:W=Ek2-Ek1=mv-mv.
3.适用范围:
(1)动能定理既适用于直线运动,也适用于曲线运动.
(2)既适用于恒力做功,也适用于变力做功.
(3)力可以是各种性质的力,既可以同时作用,也可以不同时作用.
4.应用动能定理解题的基本思路:
(1)选取研究对象,明确它的运动过程;
(2)分析研究对象的受力情况和各力的做功情况:
(3)明确研究对象在过程的初末状态的动能Ek1和Ek2;
(4)列动能定理的方程W合=Ek2-Ek1及其他必要的解题方程,进行求解.
五、重力势能
1.定义:物体的重力势能等于它所受重力与高度的乘积.
2.公式:Ep=mgh.
3.特点:
(1)系统性:重力势能是地球和物体共有的.
(2)相对性:重力势能的大小与参考平面的选取有关.重力势能的变化是绝对的,与参考平面的选取无关.
5.重力做功与重力势能变化的关系:
重力做正功时,重力势能减小;
重力做负功时,重力势能增大;重力做多少正(负)功,重力势能就减小(增大)多少,即WG=Ep1-Ep2.
六、弹性势能
1.定义:物体由于发生弹性形变而具有的能.
2.大小:弹性势能的大小与形变量及劲度系数有关,弹簧的形变量越大,劲度系数越大,弹簧的弹性势能越大.
3.弹力做功与弹性势能变化的关系:弹力做正功,弹性势能减小;弹力做负功,弹性势能增大.
七、机械能守恒定律
1.内容:在只有重力或弹力做功的物体系统内,动能与势能可以相互转化,而总的机械能保持不变.
2.表达式:
(1)守恒观点:Ek1+Ep1=Ek2+Ep2(要选零势能参考平面).
(2)转化观点:ΔEk=-ΔEp(不用选零势能参考平面).
(3)转移观点:ΔEA增=ΔEB减(不用选零势能参考平面).
3.机械能守恒的条件:只有重力(或弹力)做功或虽有其他外力做功但其他力做功的代数和为零.
4.应用机械能守恒定律解题的一般步骤:
(1)选取研究对象
(2)分析受力情况和各力做功情况,确定是否符合机械能守恒条件.
(3)确定初末状态的机械能或运动过程中物体机械能的转化情况.
(4)选择合适的表达式列出方程,进行求解.
(5)对计算结果进行必要的讨论和说明.
答案:
1、D
2、D
3、A
4、C
5、BD
6、ABC
7、(1).B
;(2)
0.25;0.24
(3)2g
8、(1)设起重机允许输出的最大功率为P0,重物达到最大速度时,拉力F0等于重力.
①
②
代入数据,有:
③
(2)匀加速运动结束时,起重机达到允许输出的最大功率,设此时重物受到的拉力为F,速度为v1,匀加速运动经历时间为t1,有:
④
⑤
⑥
由③④⑤⑥得:
⑦
t=2
s时,重物处于匀加速运动阶段,设此时速度为v2,输出功率为P,则
⑧
⑨
由⑤⑧⑨,得:P=m(g+a)at=2.04×104
W
⑩
机械能守恒定律复习(一)
2019--2020学年第二学期第
号
备课组长签字
教研组长签字:
编写人:李俊杰
班级:
第
组
姓名:
知识点复习
一、功
1.做功的两个必要条件:力和物体在力的方向上发生的位移.
2.公式:W=
适用于恒力做功.其中α为F、l方向间夹角,l为物体对地的位移.
二、功率
1.定义:功与完成这些功所用时间的比值.
2.物理意义:描述力对物体做功的快慢.
3.公式:
(1)定义式:P=
,P为时间t内的平均功率.
(2)推论式:P=
.(α为F与v的夹角)
三、动能
1.定义:物体由于运动而具有的能.
2.表达式:Ek=
.
四、动能定理
1.内容:力在一个过程中对物体做的功,等于物体在这个过程中动能的变化.
2.表达式:W=Ek2-Ek1=
.
3.适用范围:
(1)动能定理既适用于直线运动,也适用于曲线运动.
(2)既适用于恒力做功,也适用于变力做功.
(3)力可以是各种性质的力,既可以同时作用,也可以不同时作用.
4.应用动能定理解题的基本思路:
(1)选取研究对象,明确它的运动过程;
(2)分析研究对象的受力情况和各力的做功情况:
(3)明确研究对象在过程的初末状态的动能Ek1和Ek2;
(4)列动能定理的方程W合=Ek2-Ek1及其他必要的解题方程,进行求解.
五、重力势能
1.定义:物体的重力势能等于它所受重力与高度的乘积.
2.公式:Ep=
.
3.特点:
(1)系统性:重力势能是地球和物体共有的.
(2)相对性:重力势能的大小与参考平面的选取有关.重力势能的变化是绝对的,与参考平面的选取无关.
5.重力做功与重力势能变化的关系:
重力做正功时,重力势能减小;
重力做负功时,重力势能增大;重力做多少正(负)功,重力势能就减小(增大)多少,即WG=
.
六、弹性势能
1.定义:物体由于发生弹性形变而具有的能.
2.大小:弹性势能的大小与形变量及劲度系数有关,弹簧的形变量越大,劲度系数越大,弹簧的弹性势能越大.
3.弹力做功与弹性势能变化的关系:弹力做正功,弹性势能减小;弹力做负功,弹性势能增大.
七、机械能守恒定律
1.内容:在只有重力或弹力做功的物体系统内,动能与势能可以相互转化,而总的机械能保持不变.
2.表达式:
(1)守恒观点:
(要选零势能参考平面).
(2)转化观点:
(不用选零势能参考平面).
(3)转移观点:
(不用选零势能参考平面).
3.机械能守恒的条件:只有重力(或弹力)做功或虽有其他外力做功但其他力做功的代数和为零.
4.应用机械能守恒定律解题的一般步骤:
(1)选取研究对象
(2)分析受力情况和各力做功情况,确定是否符合机械能守恒条件.
(3)确定初末状态的机械能或运动过程中物体机械能的转化情况.
(4)选择合适的表达式列出方程,进行求解.
(5)对计算结果进行必要的讨论和说明.
达标检测
一、选择题
1、一人乘电梯从1楼到30楼,在此过程中经历了先加速、后匀速、再减速的运动过程,则电梯支持力对人做功情况是( )
A.加速时做正功,匀速时不做功,减速时做负功
B.加速时做正功,匀速和减速时做负功
C.加速和匀速时做正功,减速时做负功
D.始终做正功
2、选择不同的水平面作为参考平面,物体在某一位置的重力势能和某一过程中重力势能的改变量( )
A.都具有不同的数值
B.都具有相同的数值
C.前者具有相同数值,后者具有不同数值
D.前者具有不同数值,后者具有相同数值
3、某同学在桌面上用一个小钢球和一个弹簧来探究弹簧的弹性势能。弹簧一端固定(如图所示),另一端用钢球压缩弹簧后释放,钢球被弹出后落地。他发现弹簧压缩得越多,钢球被弹出得越远,由此能得出的结论应是( )
A.弹性势能与形变量有关,形变量越大,弹性势能越大
B.弹性势能与形变量有关,形变量越大,弹性势能越小
C.弹性势能与劲度系数有关,劲度系数越大,弹性势能越大
D.弹性势能与劲度系数有关,劲度系数越大,弹性势能越小
4、一物体质量为1kg,速度为10m/s,它的动能是(?????
)
A.5J??????
B.10J??????
C.50J??????
D.100J
5、(双选)下列叙述中正确的是( )
A.做匀速直线运动的物体的机械能一定守恒
B.做变速直线运动的物体的机械能可能守恒
C.外力对物体做功为零,物体的机械能一定守恒
D.系统内只有重力和弹力做功时,系统的机械能一定守恒
6、(多选)质量为4kg,的物体被人由静止开始向上提升0.25m后速度达1m/s,则下列判断正确的是(
)
A.人对物体做功12J
B.合外力对物体做功2J
C.物体克服重力做功10J
D.人对物体做的功等于物体增加的动能
二、非选择题
7、利用图示装置做“验证机械能守恒定律”实验
(1)为验证机械能是否守恒,需要比较重物下落过程中任意两点间的
A.速度变化量和高度变化量
B.动能变化量和势能变化量
(2)实验中,先接通电源,再释放重物,得到一条理想的纸带,在纸带上选连续打出的点A、B、C,测得它们到起始点O的距离如图所示,已知g=9.8m/s2,重物质量为0.5kg,打点计时器打点的周期为0.02s,从O点到B点的过程中,重物的重力势能变化量△Ep
J,动能变化量△Ek=
J.(保留两位有效数字)
(3)某同学想用下述方法研究机械能是否守恒,在纸带上选取多个计数点,测量它们到起始点O的距离h,计算对应计数点的重物速度v,描绘-h图象得到图象是一条过原点的直线,该直线的斜率接近
(填g、2g或0.5g)则可认为重物下落过程中机械能守恒。
8、修建高层建筑时常用的有塔式起重机.在起重机将质量m=5×103
kg的重物竖直吊起的过程中,重物由静止开始向上做匀加速直线运动,加速度a=0.2
m/s2,当起重机输出功率达到其允许的最大值时,保持该功率直到重物做的匀速运动.g取10m/s2,不计额外功,求
(1)起重机允许输出的最大功率.
(2)重物做匀加速直线运动所经历的时间和起重机在第2秒末的输出功率.
一、功
1.做功的两个必要条件:力和物体在力的方向上发生的位移.
2.公式:W=Flcos_α.适用于恒力做功.其中α为F、l方向间夹角,l为物体对地的位移.
二、功率
1.定义:功与完成这些功所用时间的比值.
2.物理意义:描述力对物体做功的快慢.
3.公式:
(1)定义式:P=,P为时间t内的平均功率.
(2)推论式:P=Fvcos_α.(α为F与v的夹角)
三、动能
1.定义:物体由于运动而具有的能.
2.表达式:Ek=mv2.
四、动能定理
1.内容:力在一个过程中对物体做的功,等于物体在这个过程中动能的变化.
2.表达式:W=Ek2-Ek1=mv-mv.
3.适用范围:
(1)动能定理既适用于直线运动,也适用于曲线运动.
(2)既适用于恒力做功,也适用于变力做功.
(3)力可以是各种性质的力,既可以同时作用,也可以不同时作用.
4.应用动能定理解题的基本思路:
(1)选取研究对象,明确它的运动过程;
(2)分析研究对象的受力情况和各力的做功情况:
(3)明确研究对象在过程的初末状态的动能Ek1和Ek2;
(4)列动能定理的方程W合=Ek2-Ek1及其他必要的解题方程,进行求解.
五、重力势能
1.定义:物体的重力势能等于它所受重力与高度的乘积.
2.公式:Ep=mgh.
3.特点:
(1)系统性:重力势能是地球和物体共有的.
(2)相对性:重力势能的大小与参考平面的选取有关.重力势能的变化是绝对的,与参考平面的选取无关.
5.重力做功与重力势能变化的关系:
重力做正功时,重力势能减小;
重力做负功时,重力势能增大;重力做多少正(负)功,重力势能就减小(增大)多少,即WG=Ep1-Ep2.
六、弹性势能
1.定义:物体由于发生弹性形变而具有的能.
2.大小:弹性势能的大小与形变量及劲度系数有关,弹簧的形变量越大,劲度系数越大,弹簧的弹性势能越大.
3.弹力做功与弹性势能变化的关系:弹力做正功,弹性势能减小;弹力做负功,弹性势能增大.
七、机械能守恒定律
1.内容:在只有重力或弹力做功的物体系统内,动能与势能可以相互转化,而总的机械能保持不变.
2.表达式:
(1)守恒观点:Ek1+Ep1=Ek2+Ep2(要选零势能参考平面).
(2)转化观点:ΔEk=-ΔEp(不用选零势能参考平面).
(3)转移观点:ΔEA增=ΔEB减(不用选零势能参考平面).
3.机械能守恒的条件:只有重力(或弹力)做功或虽有其他外力做功但其他力做功的代数和为零.
4.应用机械能守恒定律解题的一般步骤:
(1)选取研究对象
(2)分析受力情况和各力做功情况,确定是否符合机械能守恒条件.
(3)确定初末状态的机械能或运动过程中物体机械能的转化情况.
(4)选择合适的表达式列出方程,进行求解.
(5)对计算结果进行必要的讨论和说明.
答案:
1、D
2、D
3、A
4、C
5、BD
6、ABC
7、(1).B
;(2)
0.25;0.24
(3)2g
8、(1)设起重机允许输出的最大功率为P0,重物达到最大速度时,拉力F0等于重力.
①
②
代入数据,有:
③
(2)匀加速运动结束时,起重机达到允许输出的最大功率,设此时重物受到的拉力为F,速度为v1,匀加速运动经历时间为t1,有:
④
⑤
⑥
由③④⑤⑥得:
⑦
t=2
s时,重物处于匀加速运动阶段,设此时速度为v2,输出功率为P,则
⑧
⑨
由⑤⑧⑨,得:P=m(g+a)at=2.04×104
W
⑩
