人教版数学七年级下册 7.1.2 平面直角坐标系(3) 课件 (共27张PPT)
文档属性
| 名称 | 人教版数学七年级下册 7.1.2 平面直角坐标系(3) 课件 (共27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 608.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-27 22:57:47 | ||
图片预览








文档简介
(共27张PPT)
7.1.2平面直角坐标系
学习目标:
1、认识平面直角坐标系,了解点与坐标的对应关系
2、在给定的直角坐标系中,能根据坐标描出点的位置,能由点的位置写出点的坐标
你知道吗?
几何图形是直观地,而代数方程则比较抽象,能不能用几何图形来表示方程呢?
笛卡尔
1596—1650
法国哲学家、数学家、物理学家
坐标的思想是法国数学家笛卡尔所创立的。
笛卡尔
1596—1650
法国哲学家、数学家、物理学家
坐标的思想是法国数学家笛卡尔所创立的。
这个问题的关键是如何把组成几何图形的点和满足方程的每一组数挂上钩。他就拼命地琢磨,通过什么样的办法才能把“点”和“数”联系起来呢?
突然,他看见屋顶角上的一只蜘蛛拉着丝垂了下来,一会儿蜘蛛又顺着丝爬上去,在上面左右拉丝。蜘蛛的表演,使得笛卡尔的思路豁然开朗,他想,可以把蜘蛛看做一个点,它在屋子里可以上、下、左、右运动,能不能把蜘蛛的每一个位置有一组数确定下来呢?。
平面直角坐标系
数形结合的思想
知识点一:认识平面直角坐标系
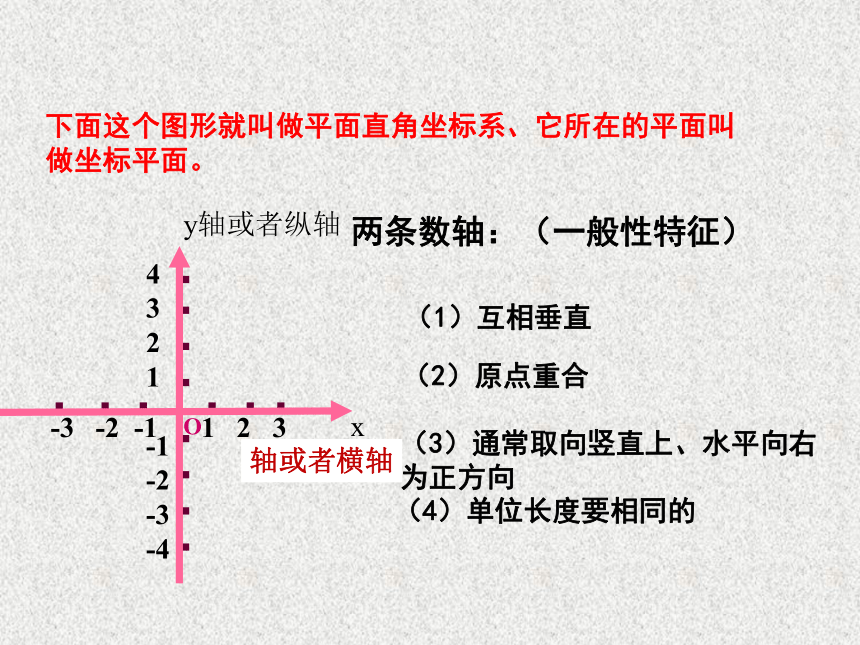
两条数轴:(一般性特征)
(1)互相垂直
(2)原点重合
(3)通常取向竖直上、水平向右
为正方向
(4)单位长度要相同的
下面这个图形就叫做平面直角坐标系、它所在的平面叫做坐标平面。
O
x
y轴或者纵轴
-3
-2
-1
1
2
3
4
3
2
1
-1
-2
-3
-4
轴或者横轴
1:概念
平面内,
组成
,水平方向的数轴称为
,习惯取向右的方向为正方向,竖直方向上的数轴称为
,习惯取向上的方向为正方向;两坐标轴的交点是平面直角坐标系的
.
2、动手画一画吧
两条互相垂直、原点重合的数轴
平面直角坐标系
x轴或横轴
y轴或纵轴
原点
X
O
练习1:下面四个图形中,是平面直角坐标系的是(
)
-3
-2
-1
1
2
3
3
2
1
-1
-2
-3
Y
X
X
Y
(A)
3
2
1
-1
-2
-3
X
Y
(B)
2
1
-1
-2
O
-3
-2
-1
1
2
3
3
2
1
-1
-2
-3
(C)
O
-3
-2
-1
1
2
3
3
2
1
-1
-2
-3
Y
(D)
O
D
探究1:点的坐标
(3,2)
p
y
3叫做点P的横坐标,
2叫做点P的纵坐标,
X
记作:P(3,2)
·
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
.Q
(2,3)
发现:
(a,b)是一对有序数对,横坐标在前,纵
坐标在后,中间用逗号隔开,不能颠倒。
N
M
知识点二:坐标平面上点的
坐标表示。
.
P
平面内任意一点P,过P点分别
向x、y轴作垂线,垂足在x轴、
y轴上对应的数a、b分别叫做
点p的横坐标、纵坐标,
则有序数对(a,b)叫做点P的坐标。
a
b
记为P(a,b)
O
X
Y
注意:横坐标写在前,纵坐标写在后,
中间用逗号隔开.
(a,b)
·
B
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
C
·
A
·
E
·
D
(
2,3
)
(
3,2
)
(
-2,1
)
(
-4,-
3
)
(
1,-
2
)
坐标是有序
数对。
练习:写出图中A、B、C、D、E各点的坐标。
·
结论:对于坐标
平面内的任意一
点都有唯一的一
对有序数对和
它对应
探究2:已知点的坐标描点
在平面直角坐标系中描出下列各点:
A(-2,3),B(2,1),C(0,4),D(3,0)
A(-2,3)
(2,-3)
练习:在平面直角坐标系中描出下列各点,
A(5,2)
、B(0,5)、C(2,-3)、
D(-2,-3)、
A
·
B
·
D
·
(0,5)
0
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
y
纵轴
x
横轴
C
·
(5,2)
(-2,-3)
结论:对与任意
一对有序数对在
坐标平面内都
有唯一的一点
和它对应。
探究3:平面直角坐标系的特点
第一象限Ⅰ
(+,+)
(-,+)
(-,-)
(+,-)
x
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
A
B
C
D
E
(-2,3)
(5,3)
(3,2)
(5,-4)
(-7,-5)
F
G
H
(-7,2)
(-5,-4)
(3,-5)
第二象限Ⅱ
探究3:平面直角坐标系的特点
第三象限Ⅲ
第四象限Ⅳ
(3,0)
(-5,0)
(0,4)
(0,-2)
知识点三:坐标平面内点的坐标符号特点
第一象限:(+,+)
第二象限:(-,+)
第三象限:(-,-)
第四象限:(+,-)
x轴上的点的纵坐标为0,表示为(x,0)
y轴上的点的横坐标为0,表示为(0,y)
直角坐标系中点的坐标的特点(在课本P44页第2题)
—
+
—
—
+
—
—
—
+
+
0
0
0
0
0
0
练一练
1.(2009年大连)在平面直角坐标系内,下列各点在第四象限的是(
)
A.(2,1)
B.(-2,1)
C.(-3,-5)
D.(3,-5)
2.已知坐标平面内点A(m,n)在第四象限,那么点B(n,m)在(
)
A.第一象限
B.第二象限.
C.第三象限
D.第四象限
D
B
O
1
1
(-3,4)
(-5,-2)
(3,-2)
(5,4)
A
C
B
D
A与D、B与C的纵坐标相同吗?为什么?A与B,C与D的横坐标相同吗?为什么?
x
y
3、写出平行四边形ABCD各个顶点的坐标。
特殊位置的点的符号特征:
平行于横轴的直线上的点的纵坐标相同;
平行于纵轴的直线上的点的横坐标相同;
横轴上的点纵坐标为0;纵轴上的点横坐标为0。
4.设点M(a,b)为平面直角坐标系中的点
当a>0,b<0时点M位于第几象限?
当ab>0时,点M位于第几象限?
当a为任意数时,且b<0时,点M直角坐标系中的位置是什么?
小结:这节课主要学习了平面直角坐标系的有
关概念和一个最基本的问题,坐标平面内的点
与有序数对是一一对应的。
1.
会根据坐标找点,会由坐标系内的点写坐标
2.掌握x轴,y轴上点的坐标的特点:
x轴上的点的纵坐标为0,表示为(x,0)
y轴上的点的横坐标为0,表示为(0,y)
第一象限:(+,+)
第二象限:(-,+)
第三象限:(-,-)
第四象限:(+,
-)
教师寄语:
同学们,其实我们每个人的人生就是一个以时间为横轴,以人的价值为纵轴的平面直角坐标系,我相信同学们一定能用自己的勤奋和智慧在这个坐标系中画出一个个光彩夺目的点,构画出辉煌的人生。
7.1.2平面直角坐标系
学习目标:
1、认识平面直角坐标系,了解点与坐标的对应关系
2、在给定的直角坐标系中,能根据坐标描出点的位置,能由点的位置写出点的坐标
你知道吗?
几何图形是直观地,而代数方程则比较抽象,能不能用几何图形来表示方程呢?
笛卡尔
1596—1650
法国哲学家、数学家、物理学家
坐标的思想是法国数学家笛卡尔所创立的。
笛卡尔
1596—1650
法国哲学家、数学家、物理学家
坐标的思想是法国数学家笛卡尔所创立的。
这个问题的关键是如何把组成几何图形的点和满足方程的每一组数挂上钩。他就拼命地琢磨,通过什么样的办法才能把“点”和“数”联系起来呢?
突然,他看见屋顶角上的一只蜘蛛拉着丝垂了下来,一会儿蜘蛛又顺着丝爬上去,在上面左右拉丝。蜘蛛的表演,使得笛卡尔的思路豁然开朗,他想,可以把蜘蛛看做一个点,它在屋子里可以上、下、左、右运动,能不能把蜘蛛的每一个位置有一组数确定下来呢?。
平面直角坐标系
数形结合的思想
知识点一:认识平面直角坐标系
两条数轴:(一般性特征)
(1)互相垂直
(2)原点重合
(3)通常取向竖直上、水平向右
为正方向
(4)单位长度要相同的
下面这个图形就叫做平面直角坐标系、它所在的平面叫做坐标平面。
O
x
y轴或者纵轴
-3
-2
-1
1
2
3
4
3
2
1
-1
-2
-3
-4
轴或者横轴
1:概念
平面内,
组成
,水平方向的数轴称为
,习惯取向右的方向为正方向,竖直方向上的数轴称为
,习惯取向上的方向为正方向;两坐标轴的交点是平面直角坐标系的
.
2、动手画一画吧
两条互相垂直、原点重合的数轴
平面直角坐标系
x轴或横轴
y轴或纵轴
原点
X
O
练习1:下面四个图形中,是平面直角坐标系的是(
)
-3
-2
-1
1
2
3
3
2
1
-1
-2
-3
Y
X
X
Y
(A)
3
2
1
-1
-2
-3
X
Y
(B)
2
1
-1
-2
O
-3
-2
-1
1
2
3
3
2
1
-1
-2
-3
(C)
O
-3
-2
-1
1
2
3
3
2
1
-1
-2
-3
Y
(D)
O
D
探究1:点的坐标
(3,2)
p
y
3叫做点P的横坐标,
2叫做点P的纵坐标,
X
记作:P(3,2)
·
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
.Q
(2,3)
发现:
(a,b)是一对有序数对,横坐标在前,纵
坐标在后,中间用逗号隔开,不能颠倒。
N
M
知识点二:坐标平面上点的
坐标表示。
.
P
平面内任意一点P,过P点分别
向x、y轴作垂线,垂足在x轴、
y轴上对应的数a、b分别叫做
点p的横坐标、纵坐标,
则有序数对(a,b)叫做点P的坐标。
a
b
记为P(a,b)
O
X
Y
注意:横坐标写在前,纵坐标写在后,
中间用逗号隔开.
(a,b)
·
B
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
C
·
A
·
E
·
D
(
2,3
)
(
3,2
)
(
-2,1
)
(
-4,-
3
)
(
1,-
2
)
坐标是有序
数对。
练习:写出图中A、B、C、D、E各点的坐标。
·
结论:对于坐标
平面内的任意一
点都有唯一的一
对有序数对和
它对应
探究2:已知点的坐标描点
在平面直角坐标系中描出下列各点:
A(-2,3),B(2,1),C(0,4),D(3,0)
A(-2,3)
(2,-3)
练习:在平面直角坐标系中描出下列各点,
A(5,2)
、B(0,5)、C(2,-3)、
D(-2,-3)、
A
·
B
·
D
·
(0,5)
0
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
y
纵轴
x
横轴
C
·
(5,2)
(-2,-3)
结论:对与任意
一对有序数对在
坐标平面内都
有唯一的一点
和它对应。
探究3:平面直角坐标系的特点
第一象限Ⅰ
(+,+)
(-,+)
(-,-)
(+,-)
x
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
A
B
C
D
E
(-2,3)
(5,3)
(3,2)
(5,-4)
(-7,-5)
F
G
H
(-7,2)
(-5,-4)
(3,-5)
第二象限Ⅱ
探究3:平面直角坐标系的特点
第三象限Ⅲ
第四象限Ⅳ
(3,0)
(-5,0)
(0,4)
(0,-2)
知识点三:坐标平面内点的坐标符号特点
第一象限:(+,+)
第二象限:(-,+)
第三象限:(-,-)
第四象限:(+,-)
x轴上的点的纵坐标为0,表示为(x,0)
y轴上的点的横坐标为0,表示为(0,y)
直角坐标系中点的坐标的特点(在课本P44页第2题)
—
+
—
—
+
—
—
—
+
+
0
0
0
0
0
0
练一练
1.(2009年大连)在平面直角坐标系内,下列各点在第四象限的是(
)
A.(2,1)
B.(-2,1)
C.(-3,-5)
D.(3,-5)
2.已知坐标平面内点A(m,n)在第四象限,那么点B(n,m)在(
)
A.第一象限
B.第二象限.
C.第三象限
D.第四象限
D
B
O
1
1
(-3,4)
(-5,-2)
(3,-2)
(5,4)
A
C
B
D
A与D、B与C的纵坐标相同吗?为什么?A与B,C与D的横坐标相同吗?为什么?
x
y
3、写出平行四边形ABCD各个顶点的坐标。
特殊位置的点的符号特征:
平行于横轴的直线上的点的纵坐标相同;
平行于纵轴的直线上的点的横坐标相同;
横轴上的点纵坐标为0;纵轴上的点横坐标为0。
4.设点M(a,b)为平面直角坐标系中的点
当a>0,b<0时点M位于第几象限?
当ab>0时,点M位于第几象限?
当a为任意数时,且b<0时,点M直角坐标系中的位置是什么?
小结:这节课主要学习了平面直角坐标系的有
关概念和一个最基本的问题,坐标平面内的点
与有序数对是一一对应的。
1.
会根据坐标找点,会由坐标系内的点写坐标
2.掌握x轴,y轴上点的坐标的特点:
x轴上的点的纵坐标为0,表示为(x,0)
y轴上的点的横坐标为0,表示为(0,y)
第一象限:(+,+)
第二象限:(-,+)
第三象限:(-,-)
第四象限:(+,
-)
教师寄语:
同学们,其实我们每个人的人生就是一个以时间为横轴,以人的价值为纵轴的平面直角坐标系,我相信同学们一定能用自己的勤奋和智慧在这个坐标系中画出一个个光彩夺目的点,构画出辉煌的人生。
