冀教版七年级数学上册2.8平面图形的旋转课件(35张)
文档属性
| 名称 | 冀教版七年级数学上册2.8平面图形的旋转课件(35张) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-27 00:00:00 | ||
图片预览









文档简介
(共35张PPT)
第二章
几何图形的初步认识
2.8
平面图形的旋转
1
课堂讲解
图形的旋转
旋转中心、旋转角
旋转的性质
2
课时流程
逐点
导讲练
课堂小结
作业提升
看左图,飞机的螺
旋桨,汽车的轮子,
放映机的胶片带动
轮,水龙头的开关
的运动,有什么共
同特点呢?
1
知识点
图形的旋转
钟表的指针及风力发电机的叶片在做什么样的运动?
知1-导
知1-导
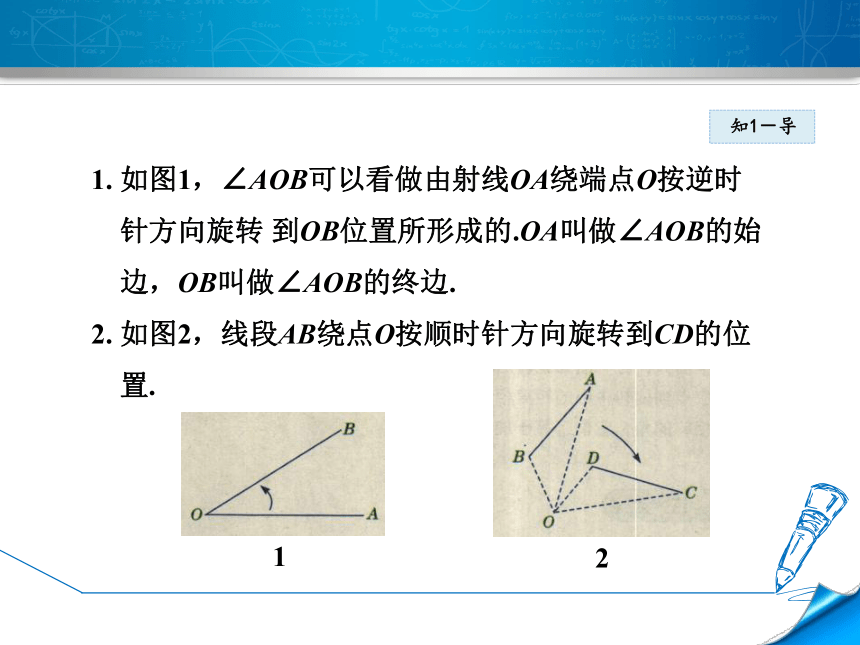
1.
如图1,∠AOB可以看做由射线OA绕端点O按逆时
针方向旋转
到OB位置所形成的.OA叫做∠AOB的始
边,OB叫做∠AOB的终边.
2.
如图2,线段AB绕点O按顺时针方向旋转到CD的位
置.
知1-讲
在平面内,一个图形绕一个定点沿某个方向转过一个角度,这
样的图形运动叫做旋转.
这个定点叫做旋转中心,转过的这个角叫做旋转角.
定义
知1-讲
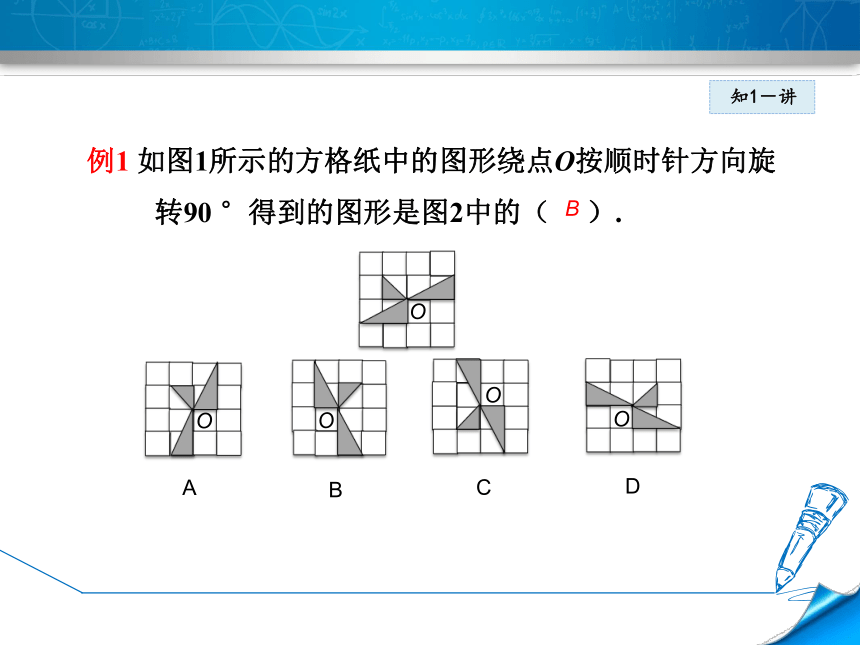
例1
如图1所示的方格纸中的图形绕点O按顺时针方向旋转90
°得到的图形是图2中的(
).
O
O
O
0
O
O
A
D
C
B
B
知1-讲
导引:
观察可知原图形是由三个直角三角形构成的,将该图形绕点O按顺时针方向旋转90°,即每个直角三角形都要按顺时针方向旋转90°,再观察A、B、C、D四个选项,与已知图形中三角形的位置对照可知,顺时针旋转90°后的图形应为B.
知1-讲
图形旋转9
0
°后的对应线段与原线段垂直,由此可得到旋转后的图形.
下列现象中,是旋转的是( )
A.车轮在水平地面上滚动
B.火车车厢的直线运动
C.电梯的上下移动
D.汽车方向盘的转动
下列现象中,属于旋转的是( )
A.钟摆的摆动
B.飞机在飞行
C.汽车在奔驰
D.小鸟飞翔
知1-练
D
1
2
A
2
知识点
旋转中心、旋转角
知2-导
如图,用一张半透明的薄纸,覆盖在画有任意
△AOB的纸上,在薄纸上画出与△AOB重合的一个三
角形.
然后用一枚图钉在点O处固定,
将薄纸绕着图钉(即点O)逆时针旋转
45°,薄纸上的三角形就旋转到了
新的位置,标上A′、B′,我们可以
认为△AOB逆时针旋转45°后变成
△A′OB′.
知2-讲
在这样的旋转过程中,你发现了什么?
从图中,可以看到点A旋转到点A′,OA旋转到
OA′,∠AOB旋转到∠A′OB′,这些都是互相对应的
点、线段与角.
此时:
点B的对应点是点______;
线段OB的对应线段是线段______;
线段AB的对应线段是线段______;
∠A的对应角是______;∠B的对应角是______;
旋转中心是点______;旋转的角度是______.
知2-讲
1.
旋转的三要素:旋转中心,旋转角,旋转方向.
要点精析:
(1)图形的旋转是由旋转中心、旋转角度及旋转的方
向决定的.
(2)旋转中心在整个旋转过程中保持不动.
(3)图形在旋转的过程中,其形状和大小不发生变化,
只是位置发生了改变.
知2-讲
(4)在旋转的过程中,图形上的每一个点同时按相同
的方向旋转相同的角度.
(5)旋转角是大于0°而小于360°的角,旋转的方向
通常说顺时针或逆时针,一组对应点与旋转中心
的连线所成的角即为旋转角.
(6)旋转中心可以是平面内的任一点.
2.
相关概念:旋转得到的图形能与原图形重合,我们
把能够重合的点叫做对应点,能够重合的线段叫做
对应线段,能够重合的角叫做对应角.
知2-讲
如图,正方形ABCD绕顶点B按顺时针方向旋转得到正方形A′BC′D′.
(1)在这个旋转过程中,旋转中心是什么?旋转角是什么?
(2)请找出图形中的对应点、对应角、对应线段.
例2
A
B
D
C
A′
D′
C′
知2-讲
导引:
一个图形经过旋转后得到一个新图形,这个新图形跟原图形能互相重合,只是位置发生了变化,但是每个点旋转前后与旋转中心的距离不变.
知2-讲
解:
(1)旋转中心是点B,∠ABA′,∠CBC′都是旋转角.
(2)对应点:点A与点A′,点C与点C′,点D与点D′,点B与点B;对应角:∠A与∠A′,∠C与∠C′,∠D与∠D′,∠ABC与∠A′BC′;对应线段:AB与A′B,AD与A′D′,CD与C′D′,BC与BC′.
知2-讲
旋转由旋转中心、旋转角和旋转方向决定,反过来,每一个旋转都有一个确定的旋转中心、旋转角和旋转方向.
1
知2-练
如图所示,AC是正方形ABCD的对角线,△ABC经过旋转后到达△AEF的位置,则旋转中心是____,旋转方向是____________,旋转角度是____,点B的对应点是____.
点A
逆时针方向
45°
点E
2
知2-练
如图,三角形AOB绕着点O旋转至三角形A′OB′,此时:
(1)点B的对应点是________;
(2)旋转中心是________,旋转
角为___________________;
(3)∠A的对应角是_______,线段OB的对应线段是__________.
点B′
点O
∠AOA′(或∠BOB
′)
∠A′
线段OB′
3
知2-练
如图,三角形ABC按顺时针方向旋转到三角形ADE的位置,以下关于旋转中心和对应点的说法中,正确的是( )
A.点A是旋转中心,点B和点E
是对应点
B.点C是旋转中心,点B和点D是对应点
C.点A是旋转中心,点C和点E是对应点
D.点D是旋转中心,点A和点D是对应点
C
知2-练
4
如图,P是正△ABC内的一点,若将△PBC绕点B旋转到△P′BA,则∠PBP′的度数是
(
)
?A.45°
B.60°
C.90°
D.120°
B
知2-讲
如图(1),点M是线段AB上一点,将线段AB绕着点M顺时针旋转90°,旋转后的线段与原线段的位置有何关系?如果逆时针旋转90°呢?
5
知2-讲
解:
如图(2),顺时针旋转90°,A′B′与AB互相垂直.
如图(3),逆时针旋转90°,A′′B′′与AB互相垂直.
知2-讲
在旋转中找出旋转中心、旋转角度及方向是研
究旋转的基础,在找角度时,也可以采取测量或计
算的方法.
3
知识点
旋转的性质
知3-导
1.
如图,已知A,B是射线OM上的两点,且OA=1
cm,
OB=2.5
cm.
(1)当OM旋转到ON位置时,点A,B分别旋转到点A',
B'的位置,请画出点A',
B'.
(2)OA和OA'
,OB和OB'
分别
有怎样的数量关系?
知2-讲
2.
如图,三角形AOB绕点O按顺时针方向旋转后得到
三角形COD,E是线段BA上一点.
(1)对应线段OB与OD,OA与OC,AB与CD分别
相等吗?
(2)∠BOD与∠AOC相等吗?
(3)画出点E的对应点F.
知3-讲
在平面内,一个图形旋转后得到的图形与原来的图形之间有如下结果:对应点到旋转中心的距离相等;每对对应点与旋转中心连线所成的角都是相等的角,它们都等于旋转角.
知3-讲
如图,在等腰直角三角形ABC中,∠B=90°,将三角形ABC绕顶点A按逆时针方向旋转60°后得到三角形AB′C′,则∠BAC′等于( )
A.60° B.105°
C.120°
D.135°
例3
B
导引:
由题意易知,∠CAC′是旋转角,故∠CAC′
=60°,所以∠BAC′=∠BAC+∠CAC′
=45°+60°=105°.
知3-讲
旋转前后的两个图形的形状、大小未发生改变,
利用旋转来解决问题时可抓住以下几点:(1)旋转中
的变(图形的位置)与不变(图形的形状、大小);(2)旋
转前后的对应关系(顶点、边、角);(3)旋转过程中的
相等关系.
如图,将三角形ABC绕点C按逆时针方向旋转25°得到三角形DEC,已知∠A=25°,∠ACE=80°,则∠B=________.
知3-练
50°
1
【中考·邵阳】将等边三角形CBA绕点C顺时针旋转∠α得到三角形CB′A′,使得B,C,A′三点在同一直线上,如图所示,则∠α的大小是___________.
知3-练
2
120°
如图,把三角形ABC绕点O按顺时针方向旋转一定角度后成为三角形A′B′C′,则下列各式:①AB=A′B′;②OB=OB′;③∠AOA′=∠COC′;④∠COB=∠A′OC′;⑤∠COA′=∠BOC′,其中成立的有( )
A.2个
B.3个
C.4个
D.5个
知3-练
3
B
1.
旋转的“三要素”:旋转中心、旋转方向、旋转角,
图形的旋转由旋转中心、旋转方向和旋转角度决定;
2.
找旋转角的方法:
(1)找出对应点;
(2)连接对应点和旋转中心;
(3)旋转中心和对应点连线的夹角即为旋转角.
必做:
完成教材P86练习T1-T2,完成教
材P87习题A组T1-T2,B组T1-T2
第二章
几何图形的初步认识
2.8
平面图形的旋转
1
课堂讲解
图形的旋转
旋转中心、旋转角
旋转的性质
2
课时流程
逐点
导讲练
课堂小结
作业提升
看左图,飞机的螺
旋桨,汽车的轮子,
放映机的胶片带动
轮,水龙头的开关
的运动,有什么共
同特点呢?
1
知识点
图形的旋转
钟表的指针及风力发电机的叶片在做什么样的运动?
知1-导
知1-导
1.
如图1,∠AOB可以看做由射线OA绕端点O按逆时
针方向旋转
到OB位置所形成的.OA叫做∠AOB的始
边,OB叫做∠AOB的终边.
2.
如图2,线段AB绕点O按顺时针方向旋转到CD的位
置.
知1-讲
在平面内,一个图形绕一个定点沿某个方向转过一个角度,这
样的图形运动叫做旋转.
这个定点叫做旋转中心,转过的这个角叫做旋转角.
定义
知1-讲
例1
如图1所示的方格纸中的图形绕点O按顺时针方向旋转90
°得到的图形是图2中的(
).
O
O
O
0
O
O
A
D
C
B
B
知1-讲
导引:
观察可知原图形是由三个直角三角形构成的,将该图形绕点O按顺时针方向旋转90°,即每个直角三角形都要按顺时针方向旋转90°,再观察A、B、C、D四个选项,与已知图形中三角形的位置对照可知,顺时针旋转90°后的图形应为B.
知1-讲
图形旋转9
0
°后的对应线段与原线段垂直,由此可得到旋转后的图形.
下列现象中,是旋转的是( )
A.车轮在水平地面上滚动
B.火车车厢的直线运动
C.电梯的上下移动
D.汽车方向盘的转动
下列现象中,属于旋转的是( )
A.钟摆的摆动
B.飞机在飞行
C.汽车在奔驰
D.小鸟飞翔
知1-练
D
1
2
A
2
知识点
旋转中心、旋转角
知2-导
如图,用一张半透明的薄纸,覆盖在画有任意
△AOB的纸上,在薄纸上画出与△AOB重合的一个三
角形.
然后用一枚图钉在点O处固定,
将薄纸绕着图钉(即点O)逆时针旋转
45°,薄纸上的三角形就旋转到了
新的位置,标上A′、B′,我们可以
认为△AOB逆时针旋转45°后变成
△A′OB′.
知2-讲
在这样的旋转过程中,你发现了什么?
从图中,可以看到点A旋转到点A′,OA旋转到
OA′,∠AOB旋转到∠A′OB′,这些都是互相对应的
点、线段与角.
此时:
点B的对应点是点______;
线段OB的对应线段是线段______;
线段AB的对应线段是线段______;
∠A的对应角是______;∠B的对应角是______;
旋转中心是点______;旋转的角度是______.
知2-讲
1.
旋转的三要素:旋转中心,旋转角,旋转方向.
要点精析:
(1)图形的旋转是由旋转中心、旋转角度及旋转的方
向决定的.
(2)旋转中心在整个旋转过程中保持不动.
(3)图形在旋转的过程中,其形状和大小不发生变化,
只是位置发生了改变.
知2-讲
(4)在旋转的过程中,图形上的每一个点同时按相同
的方向旋转相同的角度.
(5)旋转角是大于0°而小于360°的角,旋转的方向
通常说顺时针或逆时针,一组对应点与旋转中心
的连线所成的角即为旋转角.
(6)旋转中心可以是平面内的任一点.
2.
相关概念:旋转得到的图形能与原图形重合,我们
把能够重合的点叫做对应点,能够重合的线段叫做
对应线段,能够重合的角叫做对应角.
知2-讲
如图,正方形ABCD绕顶点B按顺时针方向旋转得到正方形A′BC′D′.
(1)在这个旋转过程中,旋转中心是什么?旋转角是什么?
(2)请找出图形中的对应点、对应角、对应线段.
例2
A
B
D
C
A′
D′
C′
知2-讲
导引:
一个图形经过旋转后得到一个新图形,这个新图形跟原图形能互相重合,只是位置发生了变化,但是每个点旋转前后与旋转中心的距离不变.
知2-讲
解:
(1)旋转中心是点B,∠ABA′,∠CBC′都是旋转角.
(2)对应点:点A与点A′,点C与点C′,点D与点D′,点B与点B;对应角:∠A与∠A′,∠C与∠C′,∠D与∠D′,∠ABC与∠A′BC′;对应线段:AB与A′B,AD与A′D′,CD与C′D′,BC与BC′.
知2-讲
旋转由旋转中心、旋转角和旋转方向决定,反过来,每一个旋转都有一个确定的旋转中心、旋转角和旋转方向.
1
知2-练
如图所示,AC是正方形ABCD的对角线,△ABC经过旋转后到达△AEF的位置,则旋转中心是____,旋转方向是____________,旋转角度是____,点B的对应点是____.
点A
逆时针方向
45°
点E
2
知2-练
如图,三角形AOB绕着点O旋转至三角形A′OB′,此时:
(1)点B的对应点是________;
(2)旋转中心是________,旋转
角为___________________;
(3)∠A的对应角是_______,线段OB的对应线段是__________.
点B′
点O
∠AOA′(或∠BOB
′)
∠A′
线段OB′
3
知2-练
如图,三角形ABC按顺时针方向旋转到三角形ADE的位置,以下关于旋转中心和对应点的说法中,正确的是( )
A.点A是旋转中心,点B和点E
是对应点
B.点C是旋转中心,点B和点D是对应点
C.点A是旋转中心,点C和点E是对应点
D.点D是旋转中心,点A和点D是对应点
C
知2-练
4
如图,P是正△ABC内的一点,若将△PBC绕点B旋转到△P′BA,则∠PBP′的度数是
(
)
?A.45°
B.60°
C.90°
D.120°
B
知2-讲
如图(1),点M是线段AB上一点,将线段AB绕着点M顺时针旋转90°,旋转后的线段与原线段的位置有何关系?如果逆时针旋转90°呢?
5
知2-讲
解:
如图(2),顺时针旋转90°,A′B′与AB互相垂直.
如图(3),逆时针旋转90°,A′′B′′与AB互相垂直.
知2-讲
在旋转中找出旋转中心、旋转角度及方向是研
究旋转的基础,在找角度时,也可以采取测量或计
算的方法.
3
知识点
旋转的性质
知3-导
1.
如图,已知A,B是射线OM上的两点,且OA=1
cm,
OB=2.5
cm.
(1)当OM旋转到ON位置时,点A,B分别旋转到点A',
B'的位置,请画出点A',
B'.
(2)OA和OA'
,OB和OB'
分别
有怎样的数量关系?
知2-讲
2.
如图,三角形AOB绕点O按顺时针方向旋转后得到
三角形COD,E是线段BA上一点.
(1)对应线段OB与OD,OA与OC,AB与CD分别
相等吗?
(2)∠BOD与∠AOC相等吗?
(3)画出点E的对应点F.
知3-讲
在平面内,一个图形旋转后得到的图形与原来的图形之间有如下结果:对应点到旋转中心的距离相等;每对对应点与旋转中心连线所成的角都是相等的角,它们都等于旋转角.
知3-讲
如图,在等腰直角三角形ABC中,∠B=90°,将三角形ABC绕顶点A按逆时针方向旋转60°后得到三角形AB′C′,则∠BAC′等于( )
A.60° B.105°
C.120°
D.135°
例3
B
导引:
由题意易知,∠CAC′是旋转角,故∠CAC′
=60°,所以∠BAC′=∠BAC+∠CAC′
=45°+60°=105°.
知3-讲
旋转前后的两个图形的形状、大小未发生改变,
利用旋转来解决问题时可抓住以下几点:(1)旋转中
的变(图形的位置)与不变(图形的形状、大小);(2)旋
转前后的对应关系(顶点、边、角);(3)旋转过程中的
相等关系.
如图,将三角形ABC绕点C按逆时针方向旋转25°得到三角形DEC,已知∠A=25°,∠ACE=80°,则∠B=________.
知3-练
50°
1
【中考·邵阳】将等边三角形CBA绕点C顺时针旋转∠α得到三角形CB′A′,使得B,C,A′三点在同一直线上,如图所示,则∠α的大小是___________.
知3-练
2
120°
如图,把三角形ABC绕点O按顺时针方向旋转一定角度后成为三角形A′B′C′,则下列各式:①AB=A′B′;②OB=OB′;③∠AOA′=∠COC′;④∠COB=∠A′OC′;⑤∠COA′=∠BOC′,其中成立的有( )
A.2个
B.3个
C.4个
D.5个
知3-练
3
B
1.
旋转的“三要素”:旋转中心、旋转方向、旋转角,
图形的旋转由旋转中心、旋转方向和旋转角度决定;
2.
找旋转角的方法:
(1)找出对应点;
(2)连接对应点和旋转中心;
(3)旋转中心和对应点连线的夹角即为旋转角.
必做:
完成教材P86练习T1-T2,完成教
材P87习题A组T1-T2,B组T1-T2
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
