冀教版数学七年级上册2.2点和线课件(23张)
文档属性
| 名称 | 冀教版数学七年级上册2.2点和线课件(23张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-27 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
第二章
几何图形的初步认识
1
课堂讲解
点和线段、射线、直线
直线的基本事实(性质)
2
课时流程
逐点
导讲练
课堂小结
作业提升
点和线是两种最基本的几何图形,又是构成
其他几何图形的基本
要素.
1
知识点
点和线段、射线、直线
1.
如图是某城区公园的示意
图,请在图上找出表示石刻园、展览中
心、花卉园、茶餐厅和健身区的点,并
用笔加重描出这个公
园的边界线.
知1-导
知1-导
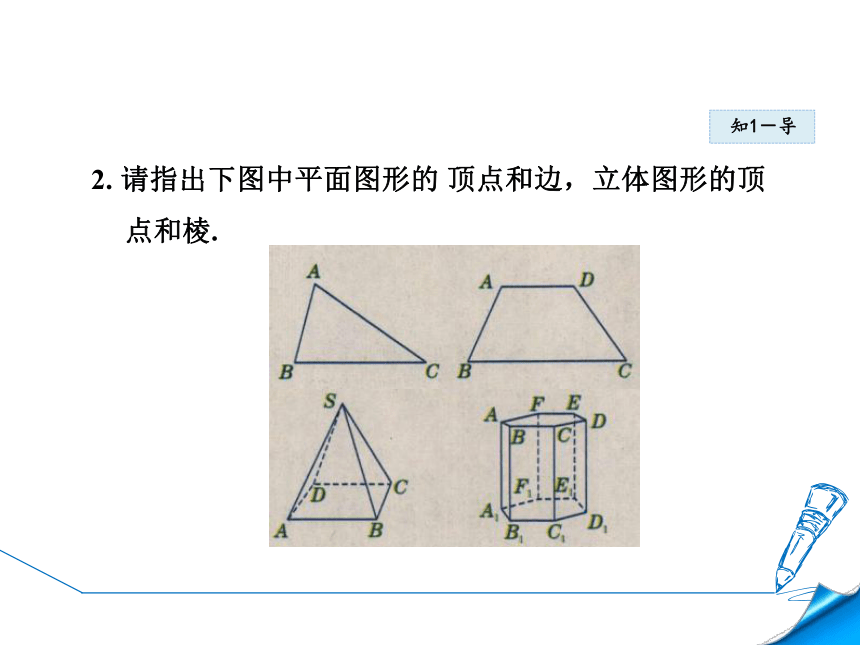
2.
请指出下图中平面图形的
顶点和边,立体图形的顶点和棱.
知1-讲
线段的直观形象是拉直的一段线.如跳高的横杆、
直尺的边沿、一段铁轨等,都给我们以线段的
形象.
点和线段的表示方法如图所示.
位于线段两端的点A,B,叫做这条线段的端点.
定义
知1-讲
如图,将线段AB沿AB方向(或BA方向)无限
延伸所形成的图形叫做射线.点A(或点B)叫做射
线的端点.
如图,将线段沿这条线段向两方无限延伸所形
成的图形,叫做直线.
定义
线段、射线各有几个端点?直线呢?
知1-讲
直线没有端点,射线有一个端点,线段有两个端点,将三者对比列表如下:
例1
如图所示,A,B,C是同一直线上的三点,下列说法正确的是( )
A
B
C
A.射线AB与射线BA是同一条射线
B.射线AB与射线BC是同一条射线
C.射线AB与射线AC是同一条射线
D.射线BA与射线BC是同一条射线
知1-讲
C
知1-讲
一条射线可用表示它的端点和射线上另一点的两个大写字母来表示,表示端点的字母必须写在前面,所以只有端点相同,并且延伸方向也相同的射线才是同一条射线.选项A、B中的两条射线端点不同,所以A、B不正确;选项D中射线BA与射线BC的延伸方向不同,所以D不正确;选项C中的两条射线的端点和延伸方向都相同,所以C正确.
如图,下列说法正确的是( )
A.直线AC与直线AD是不同的直线
B.射线AB与射线BA是同一条射线
C.线段AB与线段BA是同一条线段
D.直线AD=AB+BC+CD
知1-练
C
1
下列说法正确的是( )
A.延长直线AB
B.延长射线OA
C.延长线段AB
D.射线OA=射线AO
2
C
下列选项中,几何语言描述正确的是( )
A.直线mn与直线ab相交于点D
B.点A在直线M上
C.点A在直线AB上
D.延长直线AB
知1-练
3
C
如图,直线的表示方法( )
A.都正确
B.都错误
C.只有一个错误
D.只有一个正确
知1-练
4
D
2
知识点
直线的基本事实(性质)
知2-导
1.
用一个钉子把一根木条钉在墙上,木条能绕着钉子
转动吗?
2.用两个钉子在不同位置把木条钉在墙上,木条还能
转动吗?这种现象说明了什么?
将钉子看做一点,木条看做一条直线,我们
从上面的第一种情况可以得到:经过一点,有无
数条直线.从第二种情况可以得到:
基本事实
经过两点有一条直线,并且只有一条
直线.
知2-导
结论
知2-讲
例2
已知同一平面内有M,N,O,P四个点,请画图并回答:经过四个点中的任意两个点共能画多少条直线?
导引:M,N,O,P四个点在同一平面内的位置的情形共有三种:(1)四个点都在同一直线上;(2)有三个点在同一直线上;(3)任意三个点都不在同一直线上.因此需分类讨论.
知2-讲
解:
(1)如图①,这种情况下只能画1条直线.
(2)如图②,这种情况下能画4条直线.
(3)如图③
,这种情况下能画6条直线.
M
N
O
P
M
N
O
P
M
O
①
②
③
知2-讲
本例中M,N,O,P四个点的位置不确定,我们解题时,必须将这四个点的位置的各种情形进行分类讨论,分类时要切记不重复、不遗漏.
1
平面内有A,B,C
3个点,经过其中2个点作直线,可以作几条?
知2-练
应分为两种情况:
(1)当3个点在同一直线上时,可以作1条直线;
(2)当3个点不在同一直线上时,可以作3条直线.所以可以作1条直线或3条直线,如图所示.
解:
知2-练
2
经过同一平面内任意三点中的两点共可以画
出( )
A.一条直线
B.两条直线
C.一条或三条直线
D.三条直线
C
知2-练
3
下列说法中,错误的是( )
A.直线AB和直线BA是同一条直线
B.三条直线两两相交必有三个交点
C.线段MN是直线MN的一部分
D.三条直线两两相交,可能只有一个交点
B
几种常见几何画图语言的意义:
(1)连接AB:就是画线段AB.
(2)延长线段AB:从端点A向点B的方向延长;反向
延长线段AB:从端点B向点A的方向延长.
(3)直线过点A:先画点A,再过点A画直线;点A在
直线上:先画直线,再在直线上画点A.
(4)直线过点A,B:先画点A、点B,再过点A、点B
画直线.
1.必做:
完成教材P68练习,完成教材P68
习题A组T1-T3,B组T1-T2
2.补充:
请完成《点拨》剩余部分习题
第二章
几何图形的初步认识
1
课堂讲解
点和线段、射线、直线
直线的基本事实(性质)
2
课时流程
逐点
导讲练
课堂小结
作业提升
点和线是两种最基本的几何图形,又是构成
其他几何图形的基本
要素.
1
知识点
点和线段、射线、直线
1.
如图是某城区公园的示意
图,请在图上找出表示石刻园、展览中
心、花卉园、茶餐厅和健身区的点,并
用笔加重描出这个公
园的边界线.
知1-导
知1-导
2.
请指出下图中平面图形的
顶点和边,立体图形的顶点和棱.
知1-讲
线段的直观形象是拉直的一段线.如跳高的横杆、
直尺的边沿、一段铁轨等,都给我们以线段的
形象.
点和线段的表示方法如图所示.
位于线段两端的点A,B,叫做这条线段的端点.
定义
知1-讲
如图,将线段AB沿AB方向(或BA方向)无限
延伸所形成的图形叫做射线.点A(或点B)叫做射
线的端点.
如图,将线段沿这条线段向两方无限延伸所形
成的图形,叫做直线.
定义
线段、射线各有几个端点?直线呢?
知1-讲
直线没有端点,射线有一个端点,线段有两个端点,将三者对比列表如下:
例1
如图所示,A,B,C是同一直线上的三点,下列说法正确的是( )
A
B
C
A.射线AB与射线BA是同一条射线
B.射线AB与射线BC是同一条射线
C.射线AB与射线AC是同一条射线
D.射线BA与射线BC是同一条射线
知1-讲
C
知1-讲
一条射线可用表示它的端点和射线上另一点的两个大写字母来表示,表示端点的字母必须写在前面,所以只有端点相同,并且延伸方向也相同的射线才是同一条射线.选项A、B中的两条射线端点不同,所以A、B不正确;选项D中射线BA与射线BC的延伸方向不同,所以D不正确;选项C中的两条射线的端点和延伸方向都相同,所以C正确.
如图,下列说法正确的是( )
A.直线AC与直线AD是不同的直线
B.射线AB与射线BA是同一条射线
C.线段AB与线段BA是同一条线段
D.直线AD=AB+BC+CD
知1-练
C
1
下列说法正确的是( )
A.延长直线AB
B.延长射线OA
C.延长线段AB
D.射线OA=射线AO
2
C
下列选项中,几何语言描述正确的是( )
A.直线mn与直线ab相交于点D
B.点A在直线M上
C.点A在直线AB上
D.延长直线AB
知1-练
3
C
如图,直线的表示方法( )
A.都正确
B.都错误
C.只有一个错误
D.只有一个正确
知1-练
4
D
2
知识点
直线的基本事实(性质)
知2-导
1.
用一个钉子把一根木条钉在墙上,木条能绕着钉子
转动吗?
2.用两个钉子在不同位置把木条钉在墙上,木条还能
转动吗?这种现象说明了什么?
将钉子看做一点,木条看做一条直线,我们
从上面的第一种情况可以得到:经过一点,有无
数条直线.从第二种情况可以得到:
基本事实
经过两点有一条直线,并且只有一条
直线.
知2-导
结论
知2-讲
例2
已知同一平面内有M,N,O,P四个点,请画图并回答:经过四个点中的任意两个点共能画多少条直线?
导引:M,N,O,P四个点在同一平面内的位置的情形共有三种:(1)四个点都在同一直线上;(2)有三个点在同一直线上;(3)任意三个点都不在同一直线上.因此需分类讨论.
知2-讲
解:
(1)如图①,这种情况下只能画1条直线.
(2)如图②,这种情况下能画4条直线.
(3)如图③
,这种情况下能画6条直线.
M
N
O
P
M
N
O
P
M
O
①
②
③
知2-讲
本例中M,N,O,P四个点的位置不确定,我们解题时,必须将这四个点的位置的各种情形进行分类讨论,分类时要切记不重复、不遗漏.
1
平面内有A,B,C
3个点,经过其中2个点作直线,可以作几条?
知2-练
应分为两种情况:
(1)当3个点在同一直线上时,可以作1条直线;
(2)当3个点不在同一直线上时,可以作3条直线.所以可以作1条直线或3条直线,如图所示.
解:
知2-练
2
经过同一平面内任意三点中的两点共可以画
出( )
A.一条直线
B.两条直线
C.一条或三条直线
D.三条直线
C
知2-练
3
下列说法中,错误的是( )
A.直线AB和直线BA是同一条直线
B.三条直线两两相交必有三个交点
C.线段MN是直线MN的一部分
D.三条直线两两相交,可能只有一个交点
B
几种常见几何画图语言的意义:
(1)连接AB:就是画线段AB.
(2)延长线段AB:从端点A向点B的方向延长;反向
延长线段AB:从端点B向点A的方向延长.
(3)直线过点A:先画点A,再过点A画直线;点A在
直线上:先画直线,再在直线上画点A.
(4)直线过点A,B:先画点A、点B,再过点A、点B
画直线.
1.必做:
完成教材P68练习,完成教材P68
习题A组T1-T3,B组T1-T2
2.补充:
请完成《点拨》剩余部分习题
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
