1.1.2变化率与导数-浙江省桐庐分水高级中学高中数学人教A版选修2-2课件 (共65张PPT)
文档属性
| 名称 | 1.1.2变化率与导数-浙江省桐庐分水高级中学高中数学人教A版选修2-2课件 (共65张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-28 00:00:00 | ||
图片预览











文档简介
(共65张PPT)
1.1.2
导数的概念
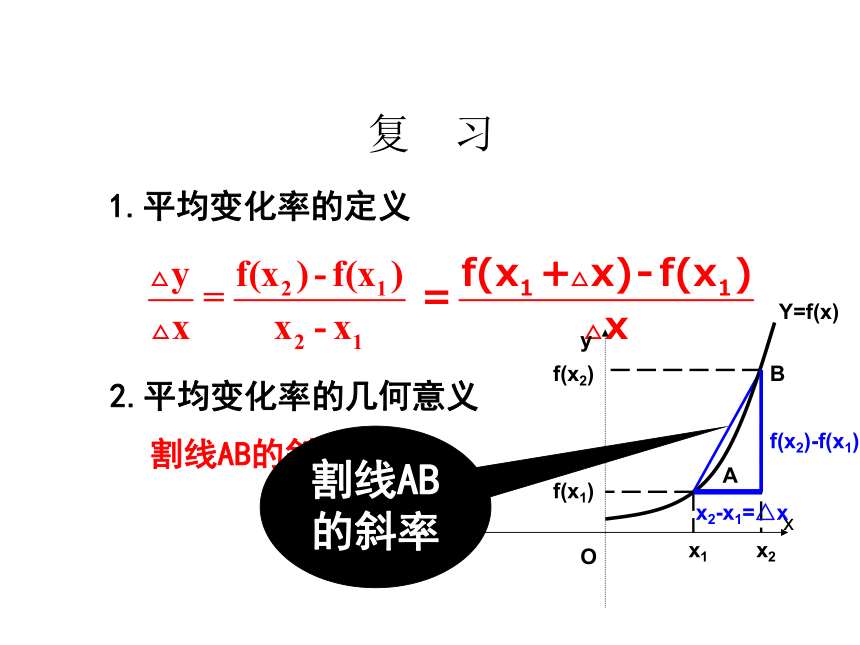
1.平均变化率的定义
复
习
2.平均变化率的几何意义
1.平均变化率的定义
复
习
2.平均变化率的几何意义
1.平均变化率的定义
复
习
2.平均变化率的几何意义
割线AB的斜率
1.平均变化率的定义
复
习
2.平均变化率的几何意义
割线AB的斜率
O
A
B
x
y
Y=f(x)
x1
x2
f(x1)
f(x2)
x2-x1=△x
f(x2)-f(x1)=△y
割线AB的斜率
3.在高台跳水运动中,运动员相对于水面的高度h(单位:米)与起跳后的时间t(单位:秒)存在函数关系
h(t)=-4.9t2+6.5t+10.
当t从2
变到2+△t
时,求运动员的平均速度,
并求△t=1,△t=0.1,△t=0.01时的平均速度。
3、在高台跳水运动中,运动员相对于水面的高度h(单位:米)与起跳后的时间t(单位:秒)存在函数关系
h(t)=-4.9t2+6.5t+10.
当t从2
变到2+△t
时,求运动员的平均速度.
3、在高台跳水运动中,运动员相对于水面的高度h(单位:米)与起跳后的时间t(单位:秒)存在函数关系
h(t)=-4.9t2+6.5t+10.
当t从2
变到2+△t
时,求运动的平均速度.
3、在高台跳水运动中,运动员相对于水面的高度h(单位:米)与起跳后的时间t(单位:秒)存在函数关系
h(t)=-4.9t2+6.5t+10.
当t从2
变到2+△t
时,求运动的平均速度.
=-4.9△t-13.1
3、在高台跳水运动中,运动员相对于水面的高度h(单位:米)与起跳后的时间t(单位:秒)存在函数关系
h(t)=-4.9t2+6.5t+10.
当t从2
变到2+△t
时,求运动的平均速度.
=-4.9△t-13.1
平均变化率近似地刻画了曲线在某一
区间上的变化趋势.
但是,
这种刻画不够精确,
有时候甚至
会相当模糊.
例如:
平均变化率近似地刻画了曲线在某一
区间上的变化趋势.
但是,
这种刻画不够精确,
有时候甚至
会相当模糊.
例如:
平均变化率近似地刻画了曲线在某一
区间上的变化趋势.
但是,
这种刻画不够精确,
有时候甚至
会相当模糊.
例如:
如何精确地刻画曲线在一点处的变化趋势呢?
3、在高台跳水运动中,运动员相对于水面的高度h(单位:米)与起跳后的时间t(单位:秒)存在函数关系
h(t)=-4.9t2+6.5t+10.
当t从2
变到2+△t
时,求运动的平均速度.
=-4.9△t-13.1
△t
=
–
0.01,
△t
=
0.01,
△t
=
–
0.001,
△t
=0.001,
△t
=
–0.0001,
△t
=0.0001,
△t
=
–
0.00001,
△t
=
0.00001,
△t
=
–
0.000001,
△t
=0.000001,
……
……
△t<0时,
在[
2+△t,
2
]这段时
间内
△t>0时,
在[2,
2
+△t
]这段时间内
为了表述方便,我们引入符号
为了表述方便,我们引入符号
为了表述方便,我们引入符号
为了表述方便,我们引入符号
1.运动员在时刻t0
的瞬时速度怎样表示?
探究
1.运动员在时刻t0
的瞬时速度怎样表示?
探究
2.
函数在
x
=
x0
处的瞬时变化率怎样表示?
探究
2.
函数在
x
=
x0
处的瞬时变化率怎样表示?
探究
4.
导数的定义:
函数
y
=
f
(x)
在
x
=
x0
处的瞬时变化率是
我们称它为函数
y
=
f
(x)
在
x
=
x0
处的导数,
即
4.
导数的定义:
注意
4.瞬时变化率与导数是同一概念的两个名称。
P
Q
导数的几何意义:
P
Q
导数的几何意义:
P
Q
导数的几何意义:
P
Q
导数的几何意义:
P
Q
切线
T
导数的几何意义:
P
Q
切线
T
导数的几何意义:
我们发现,当点Q沿着曲线无限接近点P即Δx→0时,割线PQ如果有一个极限位置PT.则我们把直线PT称为曲线在点P处的切线.
友情提示:
重点哦!
解:
解:
解:
解:
解:
解:
解:
解:
解:
解:
解:
解:
思考1:函数f(x)=x2在x=3处的切线的斜率是多少?
解:
思考1:函数f(x)=x2在x=3处的切线的斜率是多少?
解:
思考1:函数f(x)=x2在x=3处的切线的斜率是多少?
思考2:函数f(x)=x2在x=3处的切线方程式多少?
解:
思考1:函数f(x)=x2在x=3处的切线的斜率是多少?
思考2:函数f(x)=x2在x=3处的切线方程式多少?
解:
思考1:函数f(x)=x2在x=3处的切线的斜率是多少?
思考2:函数f(x)=x2在x=3处的切线方程式多少?
2.求函数在某点的导数的过程
4.求函数在某点的切线方程的过程
3.求函数在某点的导数的几何意义
1.1.2
导数的概念
1.平均变化率的定义
复
习
2.平均变化率的几何意义
1.平均变化率的定义
复
习
2.平均变化率的几何意义
1.平均变化率的定义
复
习
2.平均变化率的几何意义
割线AB的斜率
1.平均变化率的定义
复
习
2.平均变化率的几何意义
割线AB的斜率
O
A
B
x
y
Y=f(x)
x1
x2
f(x1)
f(x2)
x2-x1=△x
f(x2)-f(x1)=△y
割线AB的斜率
3.在高台跳水运动中,运动员相对于水面的高度h(单位:米)与起跳后的时间t(单位:秒)存在函数关系
h(t)=-4.9t2+6.5t+10.
当t从2
变到2+△t
时,求运动员的平均速度,
并求△t=1,△t=0.1,△t=0.01时的平均速度。
3、在高台跳水运动中,运动员相对于水面的高度h(单位:米)与起跳后的时间t(单位:秒)存在函数关系
h(t)=-4.9t2+6.5t+10.
当t从2
变到2+△t
时,求运动员的平均速度.
3、在高台跳水运动中,运动员相对于水面的高度h(单位:米)与起跳后的时间t(单位:秒)存在函数关系
h(t)=-4.9t2+6.5t+10.
当t从2
变到2+△t
时,求运动的平均速度.
3、在高台跳水运动中,运动员相对于水面的高度h(单位:米)与起跳后的时间t(单位:秒)存在函数关系
h(t)=-4.9t2+6.5t+10.
当t从2
变到2+△t
时,求运动的平均速度.
=-4.9△t-13.1
3、在高台跳水运动中,运动员相对于水面的高度h(单位:米)与起跳后的时间t(单位:秒)存在函数关系
h(t)=-4.9t2+6.5t+10.
当t从2
变到2+△t
时,求运动的平均速度.
=-4.9△t-13.1
平均变化率近似地刻画了曲线在某一
区间上的变化趋势.
但是,
这种刻画不够精确,
有时候甚至
会相当模糊.
例如:
平均变化率近似地刻画了曲线在某一
区间上的变化趋势.
但是,
这种刻画不够精确,
有时候甚至
会相当模糊.
例如:
平均变化率近似地刻画了曲线在某一
区间上的变化趋势.
但是,
这种刻画不够精确,
有时候甚至
会相当模糊.
例如:
如何精确地刻画曲线在一点处的变化趋势呢?
3、在高台跳水运动中,运动员相对于水面的高度h(单位:米)与起跳后的时间t(单位:秒)存在函数关系
h(t)=-4.9t2+6.5t+10.
当t从2
变到2+△t
时,求运动的平均速度.
=-4.9△t-13.1
△t
=
–
0.01,
△t
=
0.01,
△t
=
–
0.001,
△t
=0.001,
△t
=
–0.0001,
△t
=0.0001,
△t
=
–
0.00001,
△t
=
0.00001,
△t
=
–
0.000001,
△t
=0.000001,
……
……
△t<0时,
在[
2+△t,
2
]这段时
间内
△t>0时,
在[2,
2
+△t
]这段时间内
为了表述方便,我们引入符号
为了表述方便,我们引入符号
为了表述方便,我们引入符号
为了表述方便,我们引入符号
1.运动员在时刻t0
的瞬时速度怎样表示?
探究
1.运动员在时刻t0
的瞬时速度怎样表示?
探究
2.
函数在
x
=
x0
处的瞬时变化率怎样表示?
探究
2.
函数在
x
=
x0
处的瞬时变化率怎样表示?
探究
4.
导数的定义:
函数
y
=
f
(x)
在
x
=
x0
处的瞬时变化率是
我们称它为函数
y
=
f
(x)
在
x
=
x0
处的导数,
即
4.
导数的定义:
注意
4.瞬时变化率与导数是同一概念的两个名称。
P
Q
导数的几何意义:
P
Q
导数的几何意义:
P
Q
导数的几何意义:
P
Q
导数的几何意义:
P
Q
切线
T
导数的几何意义:
P
Q
切线
T
导数的几何意义:
我们发现,当点Q沿着曲线无限接近点P即Δx→0时,割线PQ如果有一个极限位置PT.则我们把直线PT称为曲线在点P处的切线.
友情提示:
重点哦!
解:
解:
解:
解:
解:
解:
解:
解:
解:
解:
解:
解:
思考1:函数f(x)=x2在x=3处的切线的斜率是多少?
解:
思考1:函数f(x)=x2在x=3处的切线的斜率是多少?
解:
思考1:函数f(x)=x2在x=3处的切线的斜率是多少?
思考2:函数f(x)=x2在x=3处的切线方程式多少?
解:
思考1:函数f(x)=x2在x=3处的切线的斜率是多少?
思考2:函数f(x)=x2在x=3处的切线方程式多少?
解:
思考1:函数f(x)=x2在x=3处的切线的斜率是多少?
思考2:函数f(x)=x2在x=3处的切线方程式多少?
2.求函数在某点的导数的过程
4.求函数在某点的切线方程的过程
3.求函数在某点的导数的几何意义
