1.4.2正弦、余弦函数的性质-浙江省桐庐分水高级中学高中数学人教A版必修4课件 (共24张PPT)
文档属性
| 名称 | 1.4.2正弦、余弦函数的性质-浙江省桐庐分水高级中学高中数学人教A版必修4课件 (共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 695.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-28 00:00:00 | ||
图片预览






文档简介
(共24张PPT)
正弦、余弦函数的性质(二)
任务一:
数学大咖波利亚认为:你若不能解决这问题,试先解一个有关的问题。
任务二:
它的单调性与基本初等函数的单调性有何不同?
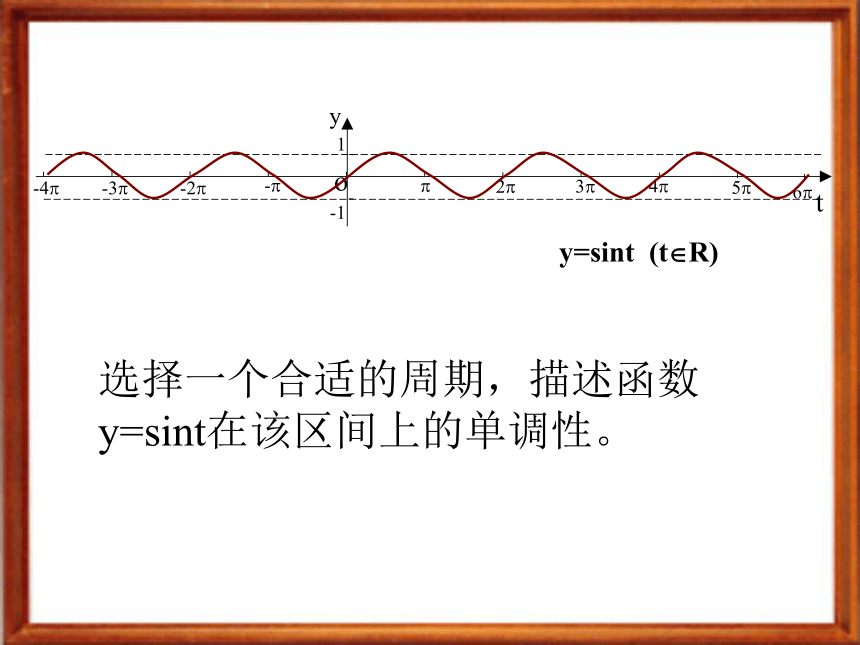
y=sint
(t?R)
选择一个合适的周期,描述函数y=sint在该区间上的单调性。
任务三:
t
y
o
-?
-1
2?
3?
4?
-2?
-3?
1
?
y=sint
-1
0
1
0
-1
t
sint
t
y
o
-?
-1
2?
3?
4?
-2?
-3?
1
?
y=sint
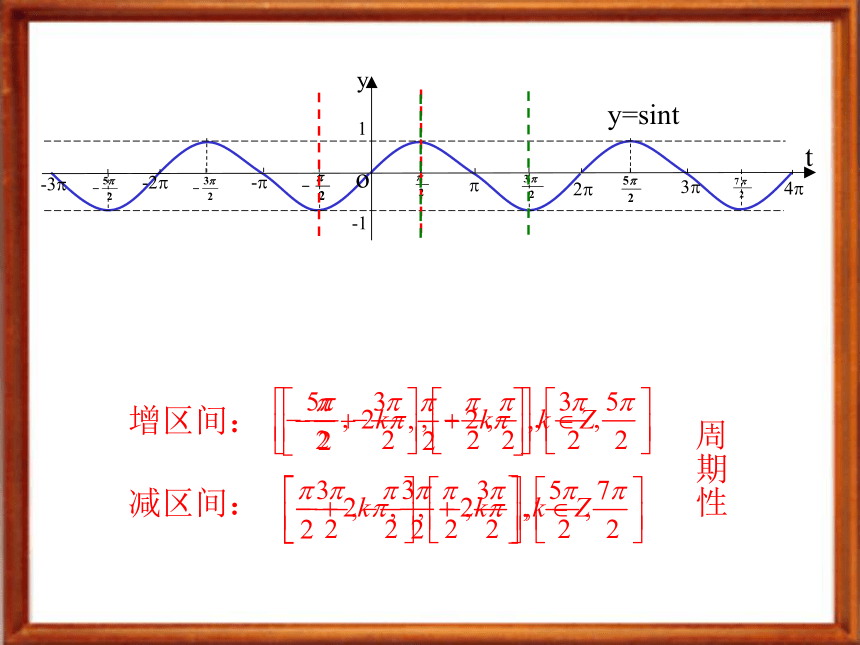
增区间:
减区间:
周期性
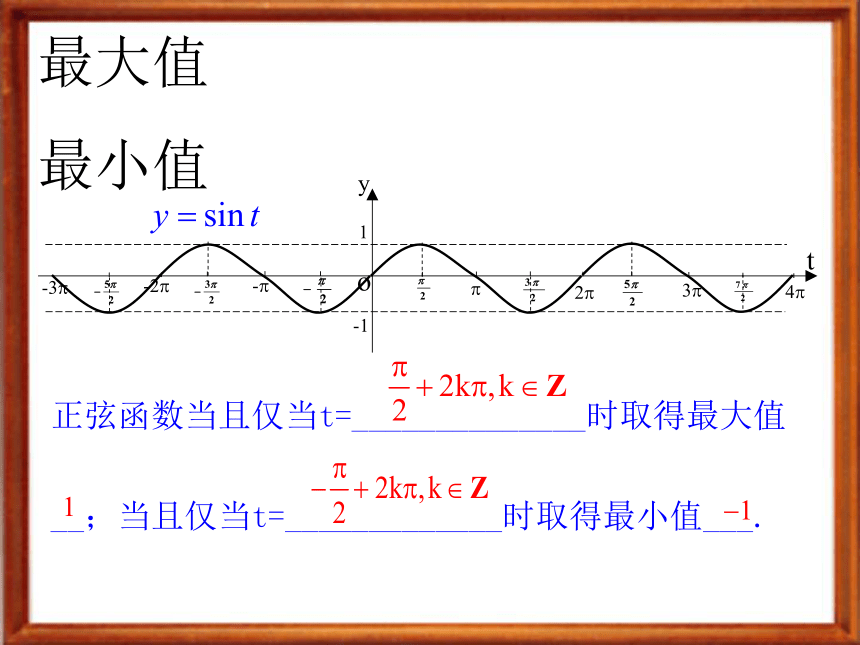
正弦函数当且仅当t=______________时取得最大值
__;当且仅当t=_____________时取得最小值___.
最大值
最小值
你有哪些方法可以求出余弦函数的单调区间?
在每个闭区间____________________上都是减函数,
y
x
o
-?
-1
2?
3?
4?
-2?
-3?
1
?
余弦函数在每个闭区间____________________上都是增函数,
其值从____增大到____;
其值从____减小到____.
提示:
例3.下列函数有最大值、最小值吗?如果有,请写出取最大值、最小值时的自变量x的集合,并说出最大值、最小值分别是什么.
解:这两个函数都有最大值、最小值.
最大值为
最小值为
使函数
取得最大值的
的集合是
(2)令
,
最大值为3.
最小值为-3.
例2.不求函数值,比较下列各组数的大小:
(1)
sin(
)
与
sin(
).
(2)
cos(
)
与cos(
).
(3)
(4)
直接单调
诱导公式:转化同一单调区间
注意符号
诱导公式:化为同名,转化同一单调区间
任务四:
?
基于这个结果你能猜一猜该函数的单调递增区间吗?如何求该函数的单调增区间?
函数
的单调递增区间是
拓展:
我们的收获:
一点知识:正余弦函数的单调性
一种本质:复合函数
一类思想:化归思想
正弦、余弦函数的性质(二)
任务一:
数学大咖波利亚认为:你若不能解决这问题,试先解一个有关的问题。
任务二:
它的单调性与基本初等函数的单调性有何不同?
y=sint
(t?R)
选择一个合适的周期,描述函数y=sint在该区间上的单调性。
任务三:
t
y
o
-?
-1
2?
3?
4?
-2?
-3?
1
?
y=sint
-1
0
1
0
-1
t
sint
t
y
o
-?
-1
2?
3?
4?
-2?
-3?
1
?
y=sint
增区间:
减区间:
周期性
正弦函数当且仅当t=______________时取得最大值
__;当且仅当t=_____________时取得最小值___.
最大值
最小值
你有哪些方法可以求出余弦函数的单调区间?
在每个闭区间____________________上都是减函数,
y
x
o
-?
-1
2?
3?
4?
-2?
-3?
1
?
余弦函数在每个闭区间____________________上都是增函数,
其值从____增大到____;
其值从____减小到____.
提示:
例3.下列函数有最大值、最小值吗?如果有,请写出取最大值、最小值时的自变量x的集合,并说出最大值、最小值分别是什么.
解:这两个函数都有最大值、最小值.
最大值为
最小值为
使函数
取得最大值的
的集合是
(2)令
,
最大值为3.
最小值为-3.
例2.不求函数值,比较下列各组数的大小:
(1)
sin(
)
与
sin(
).
(2)
cos(
)
与cos(
).
(3)
(4)
直接单调
诱导公式:转化同一单调区间
注意符号
诱导公式:化为同名,转化同一单调区间
任务四:
?
基于这个结果你能猜一猜该函数的单调递增区间吗?如何求该函数的单调增区间?
函数
的单调递增区间是
拓展:
我们的收获:
一点知识:正余弦函数的单调性
一种本质:复合函数
一类思想:化归思想
