湘教版七年级数学下册第1章二元一次方程组章末复习课件(共25张PPT)
文档属性
| 名称 | 湘教版七年级数学下册第1章二元一次方程组章末复习课件(共25张PPT) |  | |
| 格式 | rar | ||
| 文件大小 | 5.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-28 23:23:25 | ||
图片预览







文档简介
(共25张PPT)
第1章
二元一次方程组
章末复习
湘教版
七年级下册
1.含有____未知数,且含有未知数的项的次数都是______的方程叫_____________.
2.使二元一次方程的两边值_____的一对未知数的值,叫做________________
3.由_________组成,且含有____未知数的方程组,叫做_________________.
4.
同时满足二元一次方程组中各个方程的解,叫做______________________.
两个
二元一次方程
一次
相等
二元一次方程的解
一次方程
两个
二元一次方程组
二元一次方程组的解
复习导入
一、二元一次方程组的解法
(1)代入法:从一个方程中求出某一个未知数的表达式,再把它“代入”另一个方程,进行求解,这种方法叫做代入消元法,简称代入法.
(2)加减法:把方程的两边分别相加或相减消去一个未知数的方法,叫做加减消元法,简称加减法.
二、三元一次方程组的解法
消元法:通过消元,把一个较复杂的三元一次方程组转化为简单易解的阶梯形的方程组,从而通过回代得出其解,整个求解过程称为用消元法解三元一次方程组.
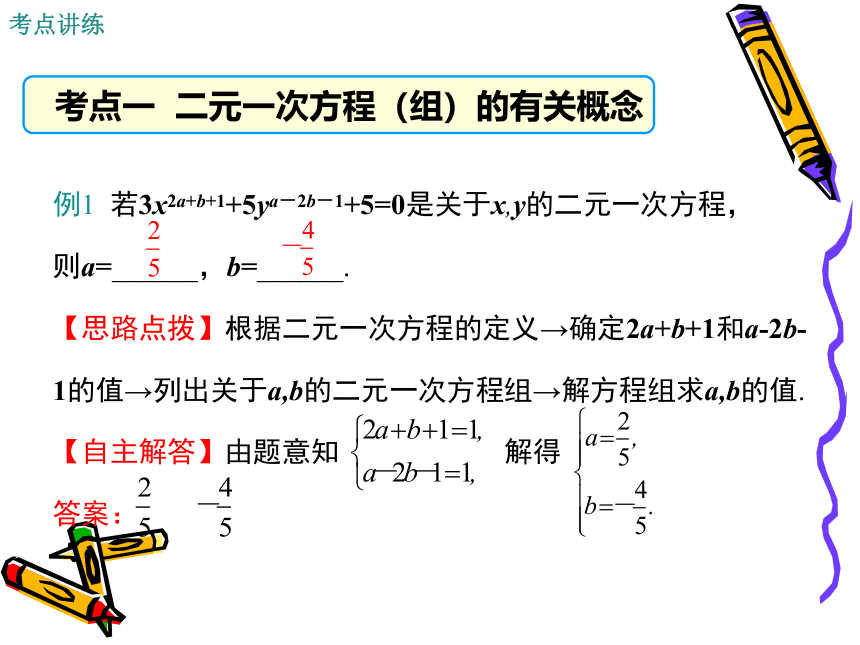
例1
若3x2a+b+1+5ya-2b-1+5=0是关于x,y的二元一次方程,
则a=______,b=______.
【思路点拨】根据二元一次方程的定义→确定2a+b+1和a-2b-1的值→列出关于a,b的二元一次方程组→解方程组求a,b的值.
【自主解答】由题意知
解得
答案:
考点讲练
考点一
二元一次方程(组)的有关概念
1.下列是二元一次方程的是
(
)
2.下列各方程组中,属于二元一次方程组的是(
)
B
C
针对训练
3.下列各对数是二元一次方程2x-5y=3的解的是
(
)
4.二元一次方程组
的解(
)
D
D
5.写出一个解为
的二元一次
方程组--------
6.已知二元一次方程:2x+3y=15
(1)用含x的代数式表示y;
(2)求出该方程的正整数解;
x=3
y=3
x=6
y=1
或者
例2
解方程组
【思路点拨】方法一:由①用y表示x,用代入消元法.
【自主解答】方法一:由①得
x=-2y.
③
把③代入②得
3×(-2y)+4y
=6.
解得
y=-3.
将y=-3代入③得
x=6,
所以原方程组的解是
考点二
等式的基本性质
考点二
解二元一次方程组
(2)
7.用适当的方法解下列方程组:
⑴
①
②
②
①
8.已知
,
①-②得:
⑴
(2)
9.已知关于x,y的方程组
的解为
求m,n的值.
解:把
代入
得
解得
例3
把一些图书分给某班学生阅读,如果每人分3本,则剩余20本;如果每人分4本,则还缺25本.这个班有多少学生?
【思路点拨】设两个未知数→找两个等量关系→列方程组→
解方程组→写答案
【自主解答】设这个班有x名学生,图书一共有y本.
答:这个班有45名学生.
解得
考点三
二元一次方程组的应用
10.某种仪器由1个A部件和1个B部件配套构成,每个工人每天可以加工A部件1
000个或者加工B部件600个,现有工人16名,应怎样安排人力,才能使每天生产的A部件和B部件配套?
解:设安排生产A部件和B部件的工人分别为x人,y人.
根据题意列方程组得
解得
答:安排生产A部件和B部件的工人分别为6人,10人.
针对训练
11.在水果店里,小李买了5
kg苹果,3
kg梨,老板少要2元,收了50元;老王买了11
kg苹果,5
kg梨,老板按九折收钱,收了90元,该店的苹果和梨的单价各是多少元?
解:设该店的苹果的单价是每千克x元,梨的单价是每千克y元.
由题意得
解得
答:该店的苹果的单价是每千克5元,梨的单价是每千克9元.
5
-1
1.已知二元一次方程组
,
则
,
。
2.已知
,
则
。
16
3.在
中,把①代入②得:
①
②
。
整体代入
复习训练
4.已知
是方程
的解,求m+n的值。
灵活应用
根据题意,灵活组建二元一次方程组
①+②得
m+n=7
①
②
5.当a为何值时,方程组
的解x、y的值互为相反数。
灵活应用
①
②
6、方程组
与方程组
的解相同,求a,b的值。
灵活应用
灵活应用
7、解关于x、y的方程组
时,
小明求得正确的解是
,
而小马因看错系数
c
解得
,
试求a,b,c的值。
拓展提高
1.已知
,则
。
6
2.已知
x
+
4y
=
0
(y≠0),求
的值.
y
–
2z
=
0
1.已知
︱4x+3y-5
︱与
︳x-3y-4
︱互为
相
反数,求x、y的值。
2.已知
3ay+5b3x与-5a2xb2-4y是同类项,
求x、y的值。
4x+3y-5=0
x-3y-4=0
y+5=2x
3x=2-4y
(X-3Y-4)2
掌握基本方法
3.已知
3ay+5b3x与-5a2xb2-4y是同类项,求x、y的值。
解:由已知得
①
②
由①得:
③
把③代入②得:
解得:
把
代入③得:
4.解方程组
(提示:x
:y=1:2可化为y=2x)
.
解:由①式得:y=2x,z=3x.
把y=2x,z=3x代入②式,得
解这个方程,得
所以原方程组的解为:
所以
y=12,z=18
解方程组:
阅读理解
①
②
解:
①+②得:
即
①-②得:
③
④
③+④得:
③-④得:
结论
正确吗?
根据方程组的特征,重构方程(组)
学有所思,感悟收获
谈谈你的收获
能说出你这节课的收获和体验
让大家与你分享吗?
谢谢,请提出宝贵意见!
第1章
二元一次方程组
章末复习
湘教版
七年级下册
1.含有____未知数,且含有未知数的项的次数都是______的方程叫_____________.
2.使二元一次方程的两边值_____的一对未知数的值,叫做________________
3.由_________组成,且含有____未知数的方程组,叫做_________________.
4.
同时满足二元一次方程组中各个方程的解,叫做______________________.
两个
二元一次方程
一次
相等
二元一次方程的解
一次方程
两个
二元一次方程组
二元一次方程组的解
复习导入
一、二元一次方程组的解法
(1)代入法:从一个方程中求出某一个未知数的表达式,再把它“代入”另一个方程,进行求解,这种方法叫做代入消元法,简称代入法.
(2)加减法:把方程的两边分别相加或相减消去一个未知数的方法,叫做加减消元法,简称加减法.
二、三元一次方程组的解法
消元法:通过消元,把一个较复杂的三元一次方程组转化为简单易解的阶梯形的方程组,从而通过回代得出其解,整个求解过程称为用消元法解三元一次方程组.
例1
若3x2a+b+1+5ya-2b-1+5=0是关于x,y的二元一次方程,
则a=______,b=______.
【思路点拨】根据二元一次方程的定义→确定2a+b+1和a-2b-1的值→列出关于a,b的二元一次方程组→解方程组求a,b的值.
【自主解答】由题意知
解得
答案:
考点讲练
考点一
二元一次方程(组)的有关概念
1.下列是二元一次方程的是
(
)
2.下列各方程组中,属于二元一次方程组的是(
)
B
C
针对训练
3.下列各对数是二元一次方程2x-5y=3的解的是
(
)
4.二元一次方程组
的解(
)
D
D
5.写出一个解为
的二元一次
方程组--------
6.已知二元一次方程:2x+3y=15
(1)用含x的代数式表示y;
(2)求出该方程的正整数解;
x=3
y=3
x=6
y=1
或者
例2
解方程组
【思路点拨】方法一:由①用y表示x,用代入消元法.
【自主解答】方法一:由①得
x=-2y.
③
把③代入②得
3×(-2y)+4y
=6.
解得
y=-3.
将y=-3代入③得
x=6,
所以原方程组的解是
考点二
等式的基本性质
考点二
解二元一次方程组
(2)
7.用适当的方法解下列方程组:
⑴
①
②
②
①
8.已知
,
①-②得:
⑴
(2)
9.已知关于x,y的方程组
的解为
求m,n的值.
解:把
代入
得
解得
例3
把一些图书分给某班学生阅读,如果每人分3本,则剩余20本;如果每人分4本,则还缺25本.这个班有多少学生?
【思路点拨】设两个未知数→找两个等量关系→列方程组→
解方程组→写答案
【自主解答】设这个班有x名学生,图书一共有y本.
答:这个班有45名学生.
解得
考点三
二元一次方程组的应用
10.某种仪器由1个A部件和1个B部件配套构成,每个工人每天可以加工A部件1
000个或者加工B部件600个,现有工人16名,应怎样安排人力,才能使每天生产的A部件和B部件配套?
解:设安排生产A部件和B部件的工人分别为x人,y人.
根据题意列方程组得
解得
答:安排生产A部件和B部件的工人分别为6人,10人.
针对训练
11.在水果店里,小李买了5
kg苹果,3
kg梨,老板少要2元,收了50元;老王买了11
kg苹果,5
kg梨,老板按九折收钱,收了90元,该店的苹果和梨的单价各是多少元?
解:设该店的苹果的单价是每千克x元,梨的单价是每千克y元.
由题意得
解得
答:该店的苹果的单价是每千克5元,梨的单价是每千克9元.
5
-1
1.已知二元一次方程组
,
则
,
。
2.已知
,
则
。
16
3.在
中,把①代入②得:
①
②
。
整体代入
复习训练
4.已知
是方程
的解,求m+n的值。
灵活应用
根据题意,灵活组建二元一次方程组
①+②得
m+n=7
①
②
5.当a为何值时,方程组
的解x、y的值互为相反数。
灵活应用
①
②
6、方程组
与方程组
的解相同,求a,b的值。
灵活应用
灵活应用
7、解关于x、y的方程组
时,
小明求得正确的解是
,
而小马因看错系数
c
解得
,
试求a,b,c的值。
拓展提高
1.已知
,则
。
6
2.已知
x
+
4y
=
0
(y≠0),求
的值.
y
–
2z
=
0
1.已知
︱4x+3y-5
︱与
︳x-3y-4
︱互为
相
反数,求x、y的值。
2.已知
3ay+5b3x与-5a2xb2-4y是同类项,
求x、y的值。
4x+3y-5=0
x-3y-4=0
y+5=2x
3x=2-4y
(X-3Y-4)2
掌握基本方法
3.已知
3ay+5b3x与-5a2xb2-4y是同类项,求x、y的值。
解:由已知得
①
②
由①得:
③
把③代入②得:
解得:
把
代入③得:
4.解方程组
(提示:x
:y=1:2可化为y=2x)
.
解:由①式得:y=2x,z=3x.
把y=2x,z=3x代入②式,得
解这个方程,得
所以原方程组的解为:
所以
y=12,z=18
解方程组:
阅读理解
①
②
解:
①+②得:
即
①-②得:
③
④
③+④得:
③-④得:
结论
正确吗?
根据方程组的特征,重构方程(组)
学有所思,感悟收获
谈谈你的收获
能说出你这节课的收获和体验
让大家与你分享吗?
谢谢,请提出宝贵意见!
