人教版八年级下册数学 18.1.2 三角形中位线定理课件(46张ppt)
文档属性
| 名称 | 人教版八年级下册数学 18.1.2 三角形中位线定理课件(46张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 7.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-27 20:29:34 | ||
图片预览

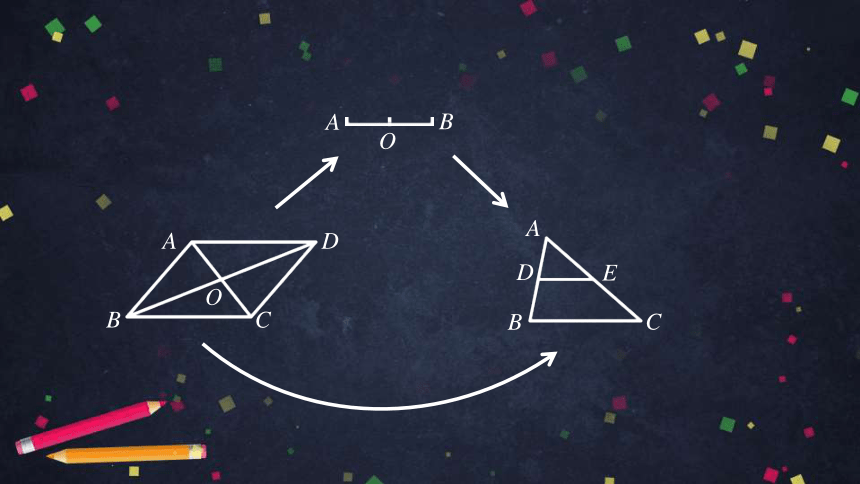




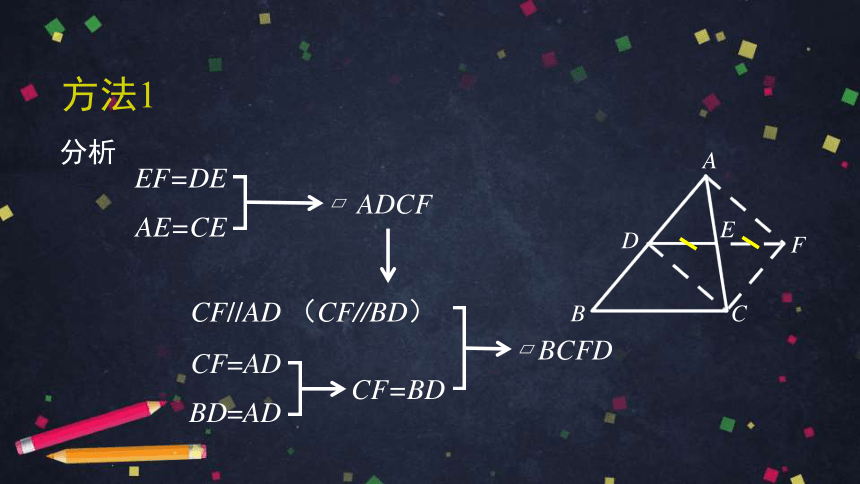
文档简介
(共46张PPT)
初二年级
数学
三角形中位线定理
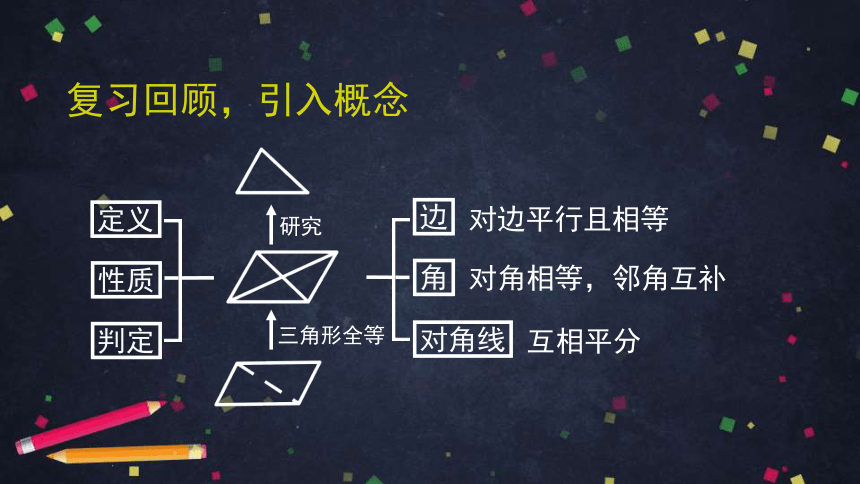
复习回顾,引入概念
三角形全等
研究
定义
性质
判定
边
角
对角线
对边平行且相等
对角相等,邻角互补
互相平分
O
A
B
C
D
A
B
O
A
B
C
D
E
如图,在△ABC中,D,E分别是AB,AC的中点,连接DE.
DE是△ABC的一条中位线.
A
B
C
D
E
三角形的中位线:
连接三角形两边中点的线段叫做三角形的中位线.
如图,在△ABC中,D,E,F分别是AB,AC,BC的中点.
连接EF,EF是△ABC的一条中位线.
连接DF,DF是△ABC的一条中位线.
F
一个三角形有三条中位线.
A
B
C
D
E
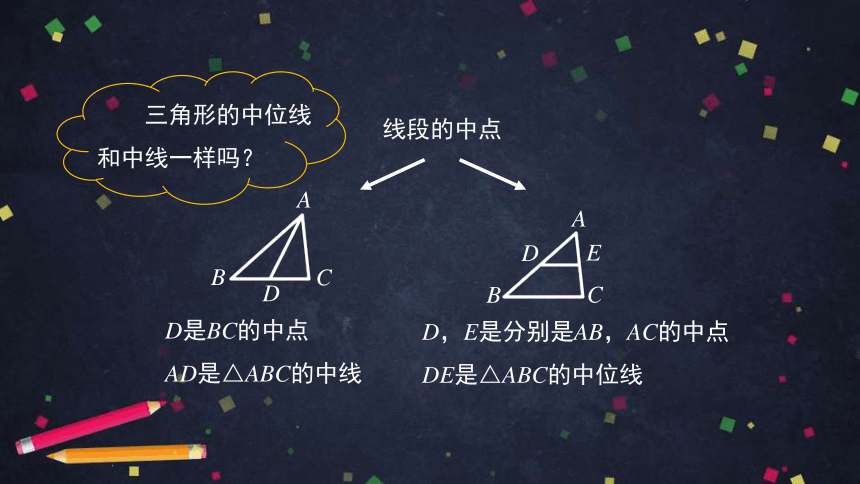
线段的中点
D是BC的中点
AD是△ABC的中线
D,E是分别是AB,AC的中点
DE是△ABC的中位线
A
B
C
D
A
B
C
D
E
三角形的中位线和中线一样吗?
提出猜想,探索定理
探究
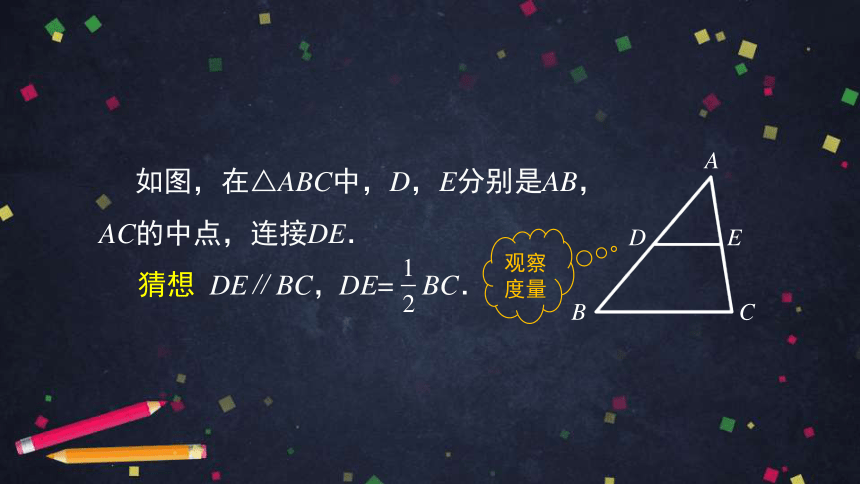
观察图形,你能发现△ABC的中位线DE与边BC的位置关系吗?
DE与BC之间有什么数量关系?
A
B
C
D
E
猜想
DE∥BC,
DE=
BC.
如图,在△ABC中,D,E分别是AB,AC的中点,连接DE.
A
B
C
D
E
观察
度量
已知:如图,D,E分别是△ABC的边AB,AC的中点.
A
B
C
D
E
求证:
DE∥BC,且DE=
BC.
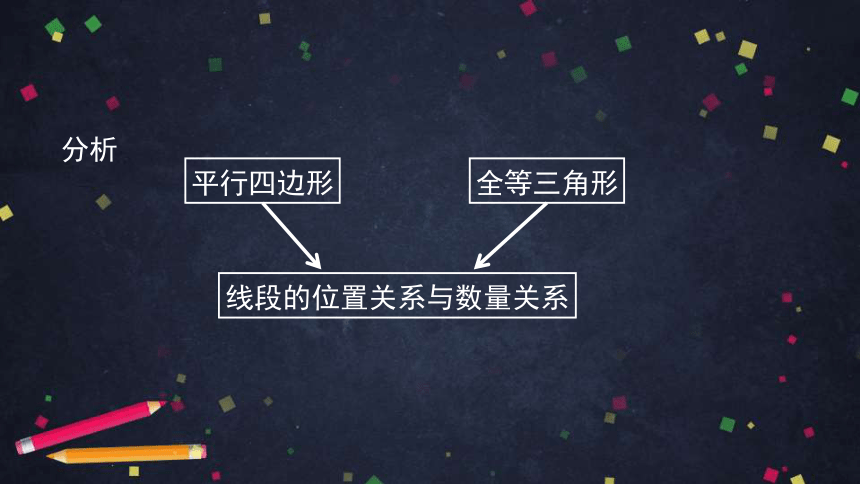
全等三角形
线段的位置关系与数量关系
平行四边形
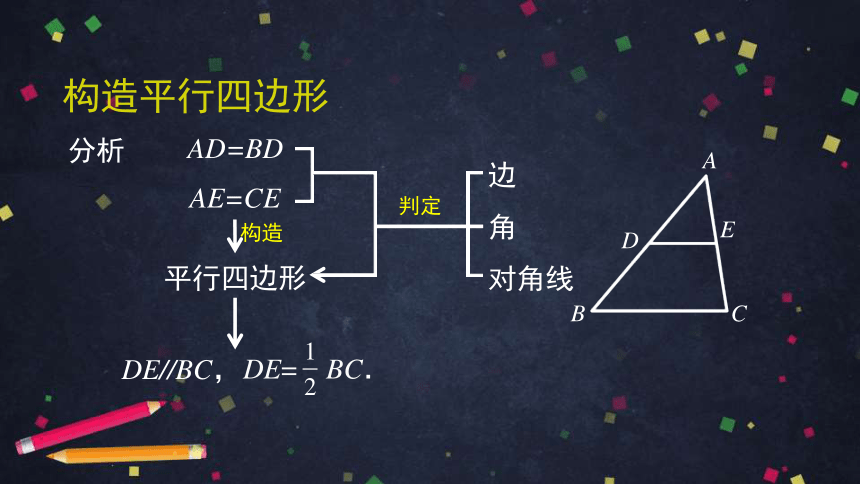
分析
分析
AD=BD
AE=CE
平行四边形
DE//BC,
构造
判定
构造平行四边形
边
角
对角线
DE=
BC.
A
B
C
D
E
F
?
ADCF
AE=CE
EF=DE
A
B
C
D
E
分析
CF//AD
(CF//BD)
CF=AD
BD=AD
CF=BD
?
BCFD
方法1
证明:延长DE到点F,使EF=DE,连接CF,DC,AF.
∵
AE=CE,EF=DE,
∴
四边形ADCF是平行四边形.
∴
CF//AD,CF=AD.
∴
CF//BD.
又
BD=AD,
∴
CF=BD.
F
A
B
C
D
E
F
A
B
C
D
E
∴
四边形BCFD是平行四边形.
∴
DF//BC,DF=BC.
又
DE=
DF,
∴
DE//BC,且DE=
BC.
F
A
B
C
D
E
如图,CF//AD,且CF=AD,
也可以表示为CF
AD.
“
”表示平行且相等.
=
=
=
=
?
BCFD
CF//BD
△ADE≌△CFE
EF=DE
∠A=∠ACF
CF=AD
AE=CE
∠AED=∠CEF
CF=BD
BD=AD
方法2
分析
F
A
B
C
D
E
延长DE到点F,使EF=DE,连接CF.
∵
AE=CE,EF=DE,
∠AED=∠CEF,
∴
△ADE≌△CFE.
∴
AD=CF,∠A=∠ECF.
∴
CF∥AB.
证明:
F
A
B
C
D
E
又
BD=AD,
∴
CF=BD.
∴
四边形BCFD是平行四边形.
∴
DF//BC,DF=BC.
又
DE=
DF,
∴
DE//BC,且DE=
BC.
F
A
B
C
D
E
A
B
C
D
E
F
F
A
B
C
D
E
?
ADCF
?
BCFD
?
BCFD
△ADE≌△CFE
F
A
B
C
D
E
?
BCFD
CF//AB(即CF//BD)
△ADE≌△CFE
CF=BD
方法3
分析
∠A=∠ECF
AE=EC
∠AED=∠CEF
CF=AD
BD=AD
过点C作CF∥BD
,与DE的延长线交于点F.
∵
CF∥BD,
∴
∠A=∠ECF.
∵
AE=CE,∠AED=∠CEF,
∴
△ADE≌△CFE.
∴
AD
=CF.
证明:
F
A
B
C
D
E
F
A
B
C
D
E
又
BD=AD,
∴
CF=BD.
∴
四边形BCFD是平行四边形.
∴
DF//BC,DF=BC.
又
DE=
DF,
∴
DE//BC,且DE=
BC.
A
B
C
D
E
三角形中位线定理:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
如图,在△ABC中,
∵
D,E分别是AB,AC的中点,
∴
DE∥BC,且DE=
BC.
过一点作已知
直线的平行线
作一条线段
等于已知线段
辅助线
构造
三角形中位线定理
平行四边形
F
A
B
C
D
E
全等三角形
F
A
B
C
D
E
分析
EF=DE
△ADE≌△CFE
△BDC≌△FCD
AE=CE
∠AED=∠CEF
∠BDC=∠FCD
CF=AD
∠A=∠ECF
CF∥AB
BD=AD
BD=CF
CD=DC
AD=BD
AE=CE
三角形中位线
定义
定理
A
B
C
D
E
DE//BC
DE=
BC
练习
如图,在△ABC中,D,E,F分别是AB,BC,AC的中点,AC=10,
BC=14,求四边形DECF的周长.
A
B
C
D
F
E
应用定理,解决问题
分析
D,E,F分别是AB,BC,AC的中点,
2(DE
+
DF)
?
DECF
A
B
C
D
F
E
DE
//AC
DF//BC
DE=
AC
DF=
BC
A
B
C
D
F
E
解:∵
D,E,F分别是AB,BC,AC的中点,
∴
DE,DF是△ABC的中位线.
∴
DE=
AC=5,DF=
BC=7,
DE//AC,DF//BC.
∴
四边形DECF是平行四边形.
∴
?
DECF的周长=2(DE+DF)
=24.
练习
如图,EF是△ABC的中位线,
BD平分∠ABC交EF于点D,ED=3,
求AB的长度.
A
B
C
D
F
E
分析
ED=BE
∠EBD=∠EDB
EF是△ABC的中位线
EF//BC
A
B
C
D
F
E
BD平分∠ABC
∠EBD=∠DBC
∠EDB=∠DBC
解:
∵
EF是△ABC的中位线,
∴
EF∥BC.
∴
∠EDB=∠DBC.
又
BD平分∠ABC,
∴
∠EBD=∠DBC.
∴
∠EBD=∠EDB.
∴
BE=ED=3.
∴
AB=2BE=6.
A
B
C
D
F
E
例
在四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.
求证:四边形EFGH是平行四边形.
A
B
C
D
F
E
H
G
A
B
C
D
F
E
H
G
分析
?
EFGH
连接对角线BD
三角形中位线
EH//FG,
EH=FG.
(AC)
(HG//EF,
HG=EF.)
证明:
连接BD.
∵
E,F,G,H分别是AB,
BC,CD,DA的中点,
∴
EH是△ABD的中位线,
FG是△CBD的中位线.
A
B
C
D
F
E
H
G
A
B
C
D
F
E
H
G
∴
EH
//BD,
FG
//BD,
EH=
BD,FG=
BD.
∴
EH
//FG,
EH=FG.
∴
四边形EFGH是平行四边形.
顺次连接四边形各边中点
平行四边形
A
B
C
D
F
E
H
G
A
B
C
D
F
E
N
M
练习
如图,在?ABCD中,E,F分别是AD,BC上的点,且DE=CF,BE和AF的交点为M,CE和DF的交点为N.
求证:MN//AD,且MN=
AD.
分析
?
EFCD,
?
ABFE
?
ABCD
MN是△AFD的中位线
A
B
C
D
F
E
N
M
MN//AD,且MN=
AD.
连接EF
.
∵
四边形ABCD是平行四边形,
∴
AD//BC,
AD=BC.
∵
DE=CF,
∴
AE=BF,
∴
四边形ABFE是平行四边形.
∴AM=FM.
A
B
C
D
F
E
N
M
证明:
A
B
C
D
F
E
N
M
又
DE=CF.
∴
四边形EFCD是平行四边形.
∴
DN=FN.
∴
MN是△AFD的中位线.
∴
MN//AD,且MN=
AD.
平行四边形
位置关系
图形构造
三角形
中位线定理
数量关系
辅助线
过一点作已知直线的垂线
过一点作已知直线的平行线
作一个角等于已知角
作一条线段等于已知线段
课堂小结
1.如图,在△ABC中,D,E,F分别是AB,BC,CA的中点.以这些点为顶点,在图中,你能画出多少个平行四边形?为什么?
课后作业
E
A
B
C
D
F
2.如图,A,B两点被池塘隔开,在AB外选一点C,连接AC和BC.怎样测出A,B两点间的距离?根据是什么?
A
B
C
A
B
C
D
F
E
G
H
O
3.如图,?ABCD的对角线AC,BD相交于点O,且E,F,G,H分别是AO,BO,CO,DO的中点.求证:四边形EFGH是平行四边形.
同学们再见!
初二年级
数学
三角形中位线定理
复习回顾,引入概念
三角形全等
研究
定义
性质
判定
边
角
对角线
对边平行且相等
对角相等,邻角互补
互相平分
O
A
B
C
D
A
B
O
A
B
C
D
E
如图,在△ABC中,D,E分别是AB,AC的中点,连接DE.
DE是△ABC的一条中位线.
A
B
C
D
E
三角形的中位线:
连接三角形两边中点的线段叫做三角形的中位线.
如图,在△ABC中,D,E,F分别是AB,AC,BC的中点.
连接EF,EF是△ABC的一条中位线.
连接DF,DF是△ABC的一条中位线.
F
一个三角形有三条中位线.
A
B
C
D
E
线段的中点
D是BC的中点
AD是△ABC的中线
D,E是分别是AB,AC的中点
DE是△ABC的中位线
A
B
C
D
A
B
C
D
E
三角形的中位线和中线一样吗?
提出猜想,探索定理
探究
观察图形,你能发现△ABC的中位线DE与边BC的位置关系吗?
DE与BC之间有什么数量关系?
A
B
C
D
E
猜想
DE∥BC,
DE=
BC.
如图,在△ABC中,D,E分别是AB,AC的中点,连接DE.
A
B
C
D
E
观察
度量
已知:如图,D,E分别是△ABC的边AB,AC的中点.
A
B
C
D
E
求证:
DE∥BC,且DE=
BC.
全等三角形
线段的位置关系与数量关系
平行四边形
分析
分析
AD=BD
AE=CE
平行四边形
DE//BC,
构造
判定
构造平行四边形
边
角
对角线
DE=
BC.
A
B
C
D
E
F
?
ADCF
AE=CE
EF=DE
A
B
C
D
E
分析
CF//AD
(CF//BD)
CF=AD
BD=AD
CF=BD
?
BCFD
方法1
证明:延长DE到点F,使EF=DE,连接CF,DC,AF.
∵
AE=CE,EF=DE,
∴
四边形ADCF是平行四边形.
∴
CF//AD,CF=AD.
∴
CF//BD.
又
BD=AD,
∴
CF=BD.
F
A
B
C
D
E
F
A
B
C
D
E
∴
四边形BCFD是平行四边形.
∴
DF//BC,DF=BC.
又
DE=
DF,
∴
DE//BC,且DE=
BC.
F
A
B
C
D
E
如图,CF//AD,且CF=AD,
也可以表示为CF
AD.
“
”表示平行且相等.
=
=
=
=
?
BCFD
CF//BD
△ADE≌△CFE
EF=DE
∠A=∠ACF
CF=AD
AE=CE
∠AED=∠CEF
CF=BD
BD=AD
方法2
分析
F
A
B
C
D
E
延长DE到点F,使EF=DE,连接CF.
∵
AE=CE,EF=DE,
∠AED=∠CEF,
∴
△ADE≌△CFE.
∴
AD=CF,∠A=∠ECF.
∴
CF∥AB.
证明:
F
A
B
C
D
E
又
BD=AD,
∴
CF=BD.
∴
四边形BCFD是平行四边形.
∴
DF//BC,DF=BC.
又
DE=
DF,
∴
DE//BC,且DE=
BC.
F
A
B
C
D
E
A
B
C
D
E
F
F
A
B
C
D
E
?
ADCF
?
BCFD
?
BCFD
△ADE≌△CFE
F
A
B
C
D
E
?
BCFD
CF//AB(即CF//BD)
△ADE≌△CFE
CF=BD
方法3
分析
∠A=∠ECF
AE=EC
∠AED=∠CEF
CF=AD
BD=AD
过点C作CF∥BD
,与DE的延长线交于点F.
∵
CF∥BD,
∴
∠A=∠ECF.
∵
AE=CE,∠AED=∠CEF,
∴
△ADE≌△CFE.
∴
AD
=CF.
证明:
F
A
B
C
D
E
F
A
B
C
D
E
又
BD=AD,
∴
CF=BD.
∴
四边形BCFD是平行四边形.
∴
DF//BC,DF=BC.
又
DE=
DF,
∴
DE//BC,且DE=
BC.
A
B
C
D
E
三角形中位线定理:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
如图,在△ABC中,
∵
D,E分别是AB,AC的中点,
∴
DE∥BC,且DE=
BC.
过一点作已知
直线的平行线
作一条线段
等于已知线段
辅助线
构造
三角形中位线定理
平行四边形
F
A
B
C
D
E
全等三角形
F
A
B
C
D
E
分析
EF=DE
△ADE≌△CFE
△BDC≌△FCD
AE=CE
∠AED=∠CEF
∠BDC=∠FCD
CF=AD
∠A=∠ECF
CF∥AB
BD=AD
BD=CF
CD=DC
AD=BD
AE=CE
三角形中位线
定义
定理
A
B
C
D
E
DE//BC
DE=
BC
练习
如图,在△ABC中,D,E,F分别是AB,BC,AC的中点,AC=10,
BC=14,求四边形DECF的周长.
A
B
C
D
F
E
应用定理,解决问题
分析
D,E,F分别是AB,BC,AC的中点,
2(DE
+
DF)
?
DECF
A
B
C
D
F
E
DE
//AC
DF//BC
DE=
AC
DF=
BC
A
B
C
D
F
E
解:∵
D,E,F分别是AB,BC,AC的中点,
∴
DE,DF是△ABC的中位线.
∴
DE=
AC=5,DF=
BC=7,
DE//AC,DF//BC.
∴
四边形DECF是平行四边形.
∴
?
DECF的周长=2(DE+DF)
=24.
练习
如图,EF是△ABC的中位线,
BD平分∠ABC交EF于点D,ED=3,
求AB的长度.
A
B
C
D
F
E
分析
ED=BE
∠EBD=∠EDB
EF是△ABC的中位线
EF//BC
A
B
C
D
F
E
BD平分∠ABC
∠EBD=∠DBC
∠EDB=∠DBC
解:
∵
EF是△ABC的中位线,
∴
EF∥BC.
∴
∠EDB=∠DBC.
又
BD平分∠ABC,
∴
∠EBD=∠DBC.
∴
∠EBD=∠EDB.
∴
BE=ED=3.
∴
AB=2BE=6.
A
B
C
D
F
E
例
在四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.
求证:四边形EFGH是平行四边形.
A
B
C
D
F
E
H
G
A
B
C
D
F
E
H
G
分析
?
EFGH
连接对角线BD
三角形中位线
EH//FG,
EH=FG.
(AC)
(HG//EF,
HG=EF.)
证明:
连接BD.
∵
E,F,G,H分别是AB,
BC,CD,DA的中点,
∴
EH是△ABD的中位线,
FG是△CBD的中位线.
A
B
C
D
F
E
H
G
A
B
C
D
F
E
H
G
∴
EH
//BD,
FG
//BD,
EH=
BD,FG=
BD.
∴
EH
//FG,
EH=FG.
∴
四边形EFGH是平行四边形.
顺次连接四边形各边中点
平行四边形
A
B
C
D
F
E
H
G
A
B
C
D
F
E
N
M
练习
如图,在?ABCD中,E,F分别是AD,BC上的点,且DE=CF,BE和AF的交点为M,CE和DF的交点为N.
求证:MN//AD,且MN=
AD.
分析
?
EFCD,
?
ABFE
?
ABCD
MN是△AFD的中位线
A
B
C
D
F
E
N
M
MN//AD,且MN=
AD.
连接EF
.
∵
四边形ABCD是平行四边形,
∴
AD//BC,
AD=BC.
∵
DE=CF,
∴
AE=BF,
∴
四边形ABFE是平行四边形.
∴AM=FM.
A
B
C
D
F
E
N
M
证明:
A
B
C
D
F
E
N
M
又
DE=CF.
∴
四边形EFCD是平行四边形.
∴
DN=FN.
∴
MN是△AFD的中位线.
∴
MN//AD,且MN=
AD.
平行四边形
位置关系
图形构造
三角形
中位线定理
数量关系
辅助线
过一点作已知直线的垂线
过一点作已知直线的平行线
作一个角等于已知角
作一条线段等于已知线段
课堂小结
1.如图,在△ABC中,D,E,F分别是AB,BC,CA的中点.以这些点为顶点,在图中,你能画出多少个平行四边形?为什么?
课后作业
E
A
B
C
D
F
2.如图,A,B两点被池塘隔开,在AB外选一点C,连接AC和BC.怎样测出A,B两点间的距离?根据是什么?
A
B
C
A
B
C
D
F
E
G
H
O
3.如图,?ABCD的对角线AC,BD相交于点O,且E,F,G,H分别是AO,BO,CO,DO的中点.求证:四边形EFGH是平行四边形.
同学们再见!
