六年级上册数学课件-第3课时 比的意义和性质西师大版(共20张PPT)
文档属性
| 名称 | 六年级上册数学课件-第3课时 比的意义和性质西师大版(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 501.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-27 22:52:29 | ||
图片预览








文档简介
(共20张PPT)
西南师大版·六年级数学上册
第3课时 比的意义和性质
1.
比的意义是什么?
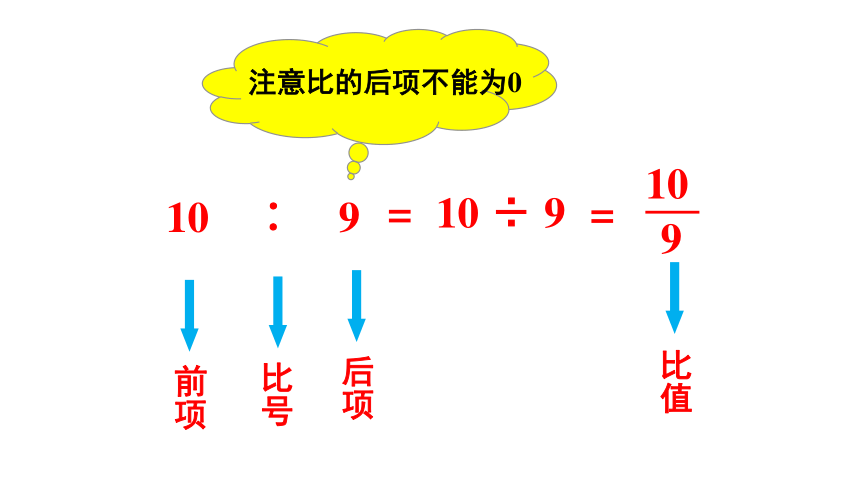
两个数相除,又叫作这两个数的比。
比是一种数量关系,相同于除法、分数,但除法是一种运算,分数是一个数。
10
∶
9
=
10
÷
9
=
10
9
前项
比号
后项
比值
长和宽的比_________;
长方形的长是
16,宽是
7。
练
习
宽和长的比_________。
16∶7
7∶16
2.比的基本性质是什么?
比的前项和后项同时乘或除以相同的数(0除外),比值不变。这叫做比的基本性质。
21∶14
=
21÷14
=
=
(21×3)∶(14×3)
=
63∶42
21∶14
=
(21×3)∶(14×3)
=
63∶42
最简整数比就是比的前项和后项是互质数。
3.最简整数比
例如
2∶3、7∶9
就是最简整数比。
把下面各比化成最简单的整数比。
2.7∶1.2
=
(2.7×10)∶(1.2×10)
=
27∶12
=
(27÷3)∶(12÷3)
=
9∶4
∶
=
∶
=
6∶5
(1)化简小数比时,都先化成整数,用比的基本性质把比的前、后项同时除以它们的最大公因数直到前、后项互质为止。
4.化简比的方法
(2)化简分数比时,先利用分数的基本性质,把分数变成整数,再化简。
5.比与除法、分数之间的关系
除法
除数
商
除号
分母
分数线
前项
后项
比值
比号
比
被除数
分数
分子
分数值
6.化简比和求比值的区别
求出所得的商
把一个比化成最简整数比的过程
前项÷后项
前、后项同时乘或除以一个不为0的数
是一个数
是一个比
求比值
化简比
意义
方法
结果
巩固练习
1.化简下列各比。
(1)27∶12
(2)2.5∶1.5
(3)
∶
(4)1.6∶
=
9∶4
=
5∶3
=
21∶20
=
64∶25
2.生产一批零件,甲单独做
8
小时完成,乙单独做
10
小时完成。
(1)甲完成任务的时间与乙完成任务的时间的最简比是(
)
(2)甲的工作效率与乙的工作效率的最简比是(
)
4∶5
5∶4
3.六年级男生和女生的人数比是
7∶5。
(1)男生人数是女生人数的(
);
(2)男生人数占全班人数的(
),女生人数占全班人数的(
);
(3)全班人数是男生人数的(
),全班人数和男生人数的比是(
);
(4)全班人数是女生人数的(
),全班人数和女生人数的比是(
)。
12∶7
12∶5
4.一种农药,用药液和水按照
1∶1500
配制而成。要配置这种农药
750.5kg,需要药液和水各多少千克?
总份数:
1+1500=1501
答:需要药液0.5kg,水750kg。
5.根据下面提供的信息,说出某两个量的比。
SOS儿童村是一个国际性民间慈善组织。拉萨等地的几个SOS儿童村在某个时期的规模如下:
SOS儿童村名称
拉萨SOS儿童村
南昌SOS儿童村
成都SOS儿童村
组建家庭个数(个)
5
12
15
收养孤儿人数(人)
180
144
116
拉萨SOS儿童村与成都SOS儿童村收养的孤儿人数的比是__________。
180∶116
SOS儿童村名称
拉萨SOS儿童村
南昌SOS儿童村
成都SOS儿童村
组建家庭个数(个)
5
12
15
收养孤儿人数(人)
180
144
116
南昌SOS儿童村收养的孤儿人数与组建家庭个数之比是__________。
144∶12
SOS儿童村名称
拉萨SOS儿童村
南昌SOS儿童村
成都SOS儿童村
组建家庭个数(个)
5
12
15
收养孤儿人数(人)
180
144
116
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
西南师大版·六年级数学上册
第3课时 比的意义和性质
1.
比的意义是什么?
两个数相除,又叫作这两个数的比。
比是一种数量关系,相同于除法、分数,但除法是一种运算,分数是一个数。
10
∶
9
=
10
÷
9
=
10
9
前项
比号
后项
比值
长和宽的比_________;
长方形的长是
16,宽是
7。
练
习
宽和长的比_________。
16∶7
7∶16
2.比的基本性质是什么?
比的前项和后项同时乘或除以相同的数(0除外),比值不变。这叫做比的基本性质。
21∶14
=
21÷14
=
=
(21×3)∶(14×3)
=
63∶42
21∶14
=
(21×3)∶(14×3)
=
63∶42
最简整数比就是比的前项和后项是互质数。
3.最简整数比
例如
2∶3、7∶9
就是最简整数比。
把下面各比化成最简单的整数比。
2.7∶1.2
=
(2.7×10)∶(1.2×10)
=
27∶12
=
(27÷3)∶(12÷3)
=
9∶4
∶
=
∶
=
6∶5
(1)化简小数比时,都先化成整数,用比的基本性质把比的前、后项同时除以它们的最大公因数直到前、后项互质为止。
4.化简比的方法
(2)化简分数比时,先利用分数的基本性质,把分数变成整数,再化简。
5.比与除法、分数之间的关系
除法
除数
商
除号
分母
分数线
前项
后项
比值
比号
比
被除数
分数
分子
分数值
6.化简比和求比值的区别
求出所得的商
把一个比化成最简整数比的过程
前项÷后项
前、后项同时乘或除以一个不为0的数
是一个数
是一个比
求比值
化简比
意义
方法
结果
巩固练习
1.化简下列各比。
(1)27∶12
(2)2.5∶1.5
(3)
∶
(4)1.6∶
=
9∶4
=
5∶3
=
21∶20
=
64∶25
2.生产一批零件,甲单独做
8
小时完成,乙单独做
10
小时完成。
(1)甲完成任务的时间与乙完成任务的时间的最简比是(
)
(2)甲的工作效率与乙的工作效率的最简比是(
)
4∶5
5∶4
3.六年级男生和女生的人数比是
7∶5。
(1)男生人数是女生人数的(
);
(2)男生人数占全班人数的(
),女生人数占全班人数的(
);
(3)全班人数是男生人数的(
),全班人数和男生人数的比是(
);
(4)全班人数是女生人数的(
),全班人数和女生人数的比是(
)。
12∶7
12∶5
4.一种农药,用药液和水按照
1∶1500
配制而成。要配置这种农药
750.5kg,需要药液和水各多少千克?
总份数:
1+1500=1501
答:需要药液0.5kg,水750kg。
5.根据下面提供的信息,说出某两个量的比。
SOS儿童村是一个国际性民间慈善组织。拉萨等地的几个SOS儿童村在某个时期的规模如下:
SOS儿童村名称
拉萨SOS儿童村
南昌SOS儿童村
成都SOS儿童村
组建家庭个数(个)
5
12
15
收养孤儿人数(人)
180
144
116
拉萨SOS儿童村与成都SOS儿童村收养的孤儿人数的比是__________。
180∶116
SOS儿童村名称
拉萨SOS儿童村
南昌SOS儿童村
成都SOS儿童村
组建家庭个数(个)
5
12
15
收养孤儿人数(人)
180
144
116
南昌SOS儿童村收养的孤儿人数与组建家庭个数之比是__________。
144∶12
SOS儿童村名称
拉萨SOS儿童村
南昌SOS儿童村
成都SOS儿童村
组建家庭个数(个)
5
12
15
收养孤儿人数(人)
180
144
116
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
