人教A版必修5第三章3.2基本不等式(共22张PPT)
文档属性
| 名称 | 人教A版必修5第三章3.2基本不等式(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 953.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-29 12:06:54 | ||
图片预览







文档简介
(共22张PPT)
3.2均值不等式
ICM2002会标
如图,这是在北京召开的第22届国际数学家大会会标.会标根据中国古代数学家赵爽的弦图设计的,颜色的明暗使它看上去象一个风车,代表中国人民热情好客。
看一看:这会标中含有怎样的几何图形
想一想:你能否在这个图案中找出一些相等关系或不等关系?
直角三角形和正方形
四个直角三角形的面积相等
直角三角形的直角边不相等
大正方形的面积大于四个直角三角形的面积
a
b
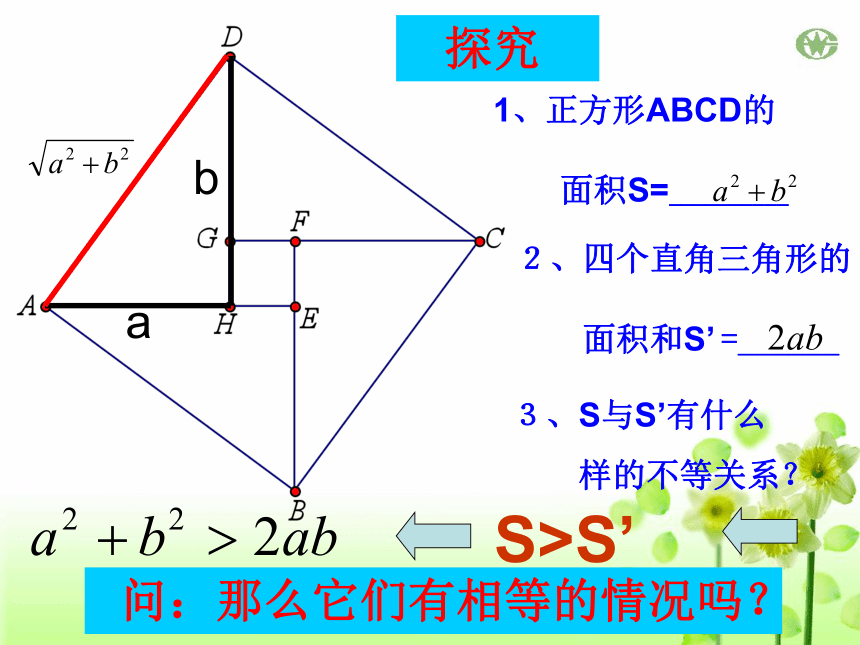
1、正方形ABCD的
面积S=__________
2、四个直角三角形的
面积和S’
=______
3、S与S’有什么
样的不等关系?
探究
S>S’
问:那么它们有相等的情况吗?
b
a
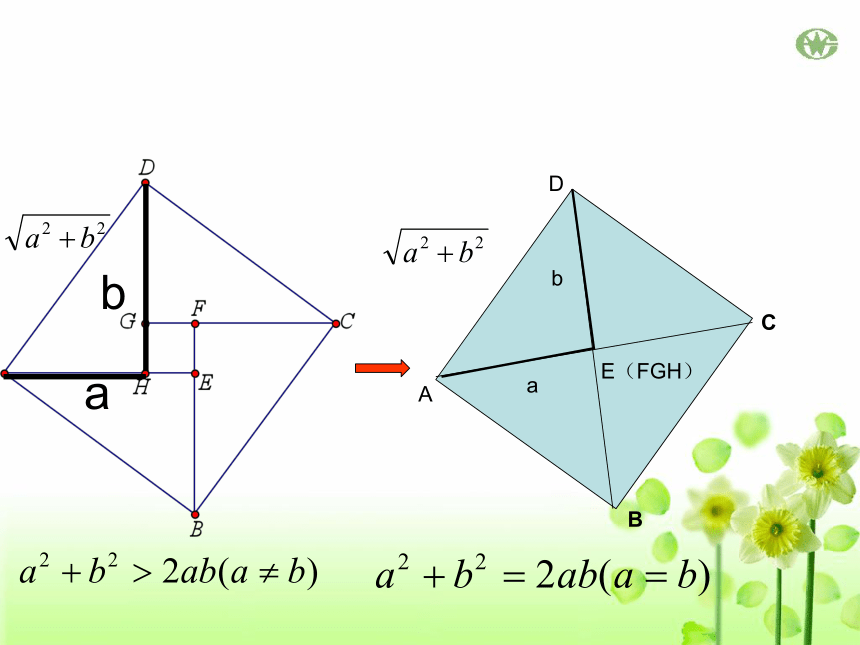
a2+b2≥2ab
思考:
(1)该结论成立的条件是什么
?
若a,b∈R,那么
(2)公式中等号成立的条件是什么?
(当且仅当a=b时,取“=”号)
a2+b2≥2ab
思考:你能给出不等式
的证明吗?
若a,b∈R,那么a2+b2≥2ab
(当且仅当a=b时,等号成立)
思考3
:不等式左右两边有何种运算结构?
任意两数的平方和不小于它们的积的两倍
由此公式,我们可以变形为
若a,b∈R,那么a2+b2≥2ab
(当且仅当a=b时,等号成立)
若a>0
b>0
(当且仅当a=b时,等号成立)
那么a
+
b
≥2
均值不等式的证明
1
作差比较法;
2
换元法;
3
反证法;
4
几何解释法。
探究2:
A
B
C
D
E
1、如图,AB是圆的直径,C是AB上与A、B不重合的一点,AC=a,CB=b,过点C作垂直于AB的弦DE,连AD,BD,
则CD=__,半径=____
a
b
半弦不大于半径
O
基本不等式
当且仅当a=b时,等号成立。
1.两个正数的算术平均数不小于它们的几何平均数.
2.两个正数的等差中项不小于它们的等比中项
3.变形用
均值不等式的变式应用1
均值不等式的变式应用1
均值不等式的变式应用2
均值不等式的变式应用2
均值不等式的实际应用
例3
(1)一个矩形的面积为100m2,问这个矩形的长、宽各为多少时,矩形的周长最短?最短周长是多少?
(2)已知矩形的周长是36m,问这个矩形的长、宽各为多少时,矩形的面积最大?最大面积是多少?
1.已知x>0,
y>0,
xy=24,
求4x+6y的最小值,并说明此时x,y的值.
2
.
已知a+b=4,求y=2a+2b的最小值。
当堂检测
当x=6,y=4时,最小值为48
最小值为8
思考:我们已经知道
那么,在
的条件下,你能比较
的大小吗?
由此,你可以得到什么结论呢?
3.2均值不等式
ICM2002会标
如图,这是在北京召开的第22届国际数学家大会会标.会标根据中国古代数学家赵爽的弦图设计的,颜色的明暗使它看上去象一个风车,代表中国人民热情好客。
看一看:这会标中含有怎样的几何图形
想一想:你能否在这个图案中找出一些相等关系或不等关系?
直角三角形和正方形
四个直角三角形的面积相等
直角三角形的直角边不相等
大正方形的面积大于四个直角三角形的面积
a
b
1、正方形ABCD的
面积S=__________
2、四个直角三角形的
面积和S’
=______
3、S与S’有什么
样的不等关系?
探究
S>S’
问:那么它们有相等的情况吗?
b
a
a2+b2≥2ab
思考:
(1)该结论成立的条件是什么
?
若a,b∈R,那么
(2)公式中等号成立的条件是什么?
(当且仅当a=b时,取“=”号)
a2+b2≥2ab
思考:你能给出不等式
的证明吗?
若a,b∈R,那么a2+b2≥2ab
(当且仅当a=b时,等号成立)
思考3
:不等式左右两边有何种运算结构?
任意两数的平方和不小于它们的积的两倍
由此公式,我们可以变形为
若a,b∈R,那么a2+b2≥2ab
(当且仅当a=b时,等号成立)
若a>0
b>0
(当且仅当a=b时,等号成立)
那么a
+
b
≥2
均值不等式的证明
1
作差比较法;
2
换元法;
3
反证法;
4
几何解释法。
探究2:
A
B
C
D
E
1、如图,AB是圆的直径,C是AB上与A、B不重合的一点,AC=a,CB=b,过点C作垂直于AB的弦DE,连AD,BD,
则CD=__,半径=____
a
b
半弦不大于半径
O
基本不等式
当且仅当a=b时,等号成立。
1.两个正数的算术平均数不小于它们的几何平均数.
2.两个正数的等差中项不小于它们的等比中项
3.变形用
均值不等式的变式应用1
均值不等式的变式应用1
均值不等式的变式应用2
均值不等式的变式应用2
均值不等式的实际应用
例3
(1)一个矩形的面积为100m2,问这个矩形的长、宽各为多少时,矩形的周长最短?最短周长是多少?
(2)已知矩形的周长是36m,问这个矩形的长、宽各为多少时,矩形的面积最大?最大面积是多少?
1.已知x>0,
y>0,
xy=24,
求4x+6y的最小值,并说明此时x,y的值.
2
.
已知a+b=4,求y=2a+2b的最小值。
当堂检测
当x=6,y=4时,最小值为48
最小值为8
思考:我们已经知道
那么,在
的条件下,你能比较
的大小吗?
由此,你可以得到什么结论呢?
