苏科版数学初二下册7.4 频数分布表和频数分布直方图巩固练习(含答案)
文档属性
| 名称 | 苏科版数学初二下册7.4 频数分布表和频数分布直方图巩固练习(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 310.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-29 00:00:00 | ||
图片预览



文档简介
直方图——巩固练习
【巩固练习】
一、选择题
1.为了绘出一批数据的频数分布直方图,首先计算出这批数据的变动范围是指数据的
(
)
A.最大值
B.最小值
C.最大值与最小值的差
D.个数
2.在频数分布直方图中,各小矩形的面积等于
(
)
A.相应各组的频数
B.组数
C.相应各组的频率
D.组距
3.已知一组数据的最大值为46,最小值为27,在绘制频数分布直方
图时,取组距为3,则这组数据应分成
( )
A.5组
B.6组
C.7组
D.8组
4.某班50名学生期末考试数学成绩的频数分布直方图如图所示,对图中提供的信息做出如下判断:
①成绩在50~60分段的人数与90~100分段的人数相等;
②从左到右数,第4小组的频率是0.03;
③成绩在80分以上的学生有20人;
④及格率为90%.
其中正确的判断有
(
)
A.4个
B.3个
C.2个
D.1个
5.在样本频数分布直方图中,有11个小长方形.若中间的小长方形
的面积等于其他10个小长方形面积之和的,且样本容量为160个,则中间的一组的频数为
(
)
A.0.2
B.32
C.0.25
D.40
6.
某学校随机抽取了同龄的60名学生,对其身高进行测量,测量数据(均为整数)进行整理后绘成频率分布直方图(如下图),图中自左向右各小组数据的频率依次为:0.017,0.050,0.100,0.133,0.300,0.183,0.167,0.050.则身高在157.5以上的学生有( )
A.18人
B.24人
C.39人
D.42人
7.有40个数据,其中最大值为35,最小值为15,若取组距为4,则应该分的组数是
(
)
A.4
B.5
C.6
D.7
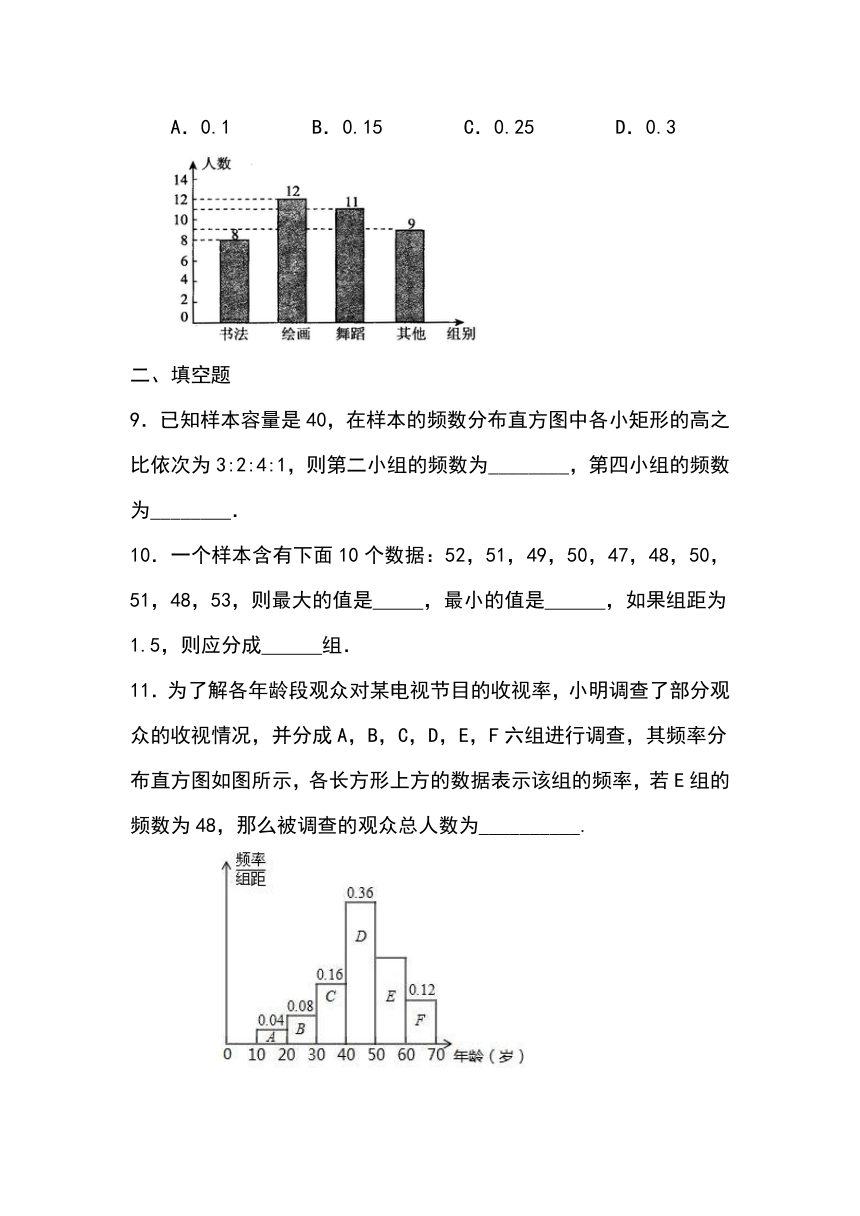
学校为了解七年级学生参加课外兴趣小组活动情况,随机调查了
40名学生,将结果绘制成了如图所示的频数分布直方图,则参加绘画兴趣小组的频率是
(
)
A.0.1
B.0.15
C.0.25
D.0.3
二、填空题
9.已知样本容量是40,在样本的频数分布直方图中各小矩形的高之
比依次为3:2:4:1,则第二小组的频数为________,第四小组的频数
为________.
10.一个样本含有下面10个数据:52,51,49,50,47,48,50,51,48,53,则最大的值是
,最小的值是
,如果组距为1.5,则应分成
组.
11.为了解各年龄段观众对某电视节目的收视率,小明调查了部分观
众的收视情况,并分成A,B,C,D,E,F六组进行调查,其频率分
布直方图如图所示,各长方形上方的数据表示该组的频率,若E组的
频数为48,那么被调查的观众总人数为__________.
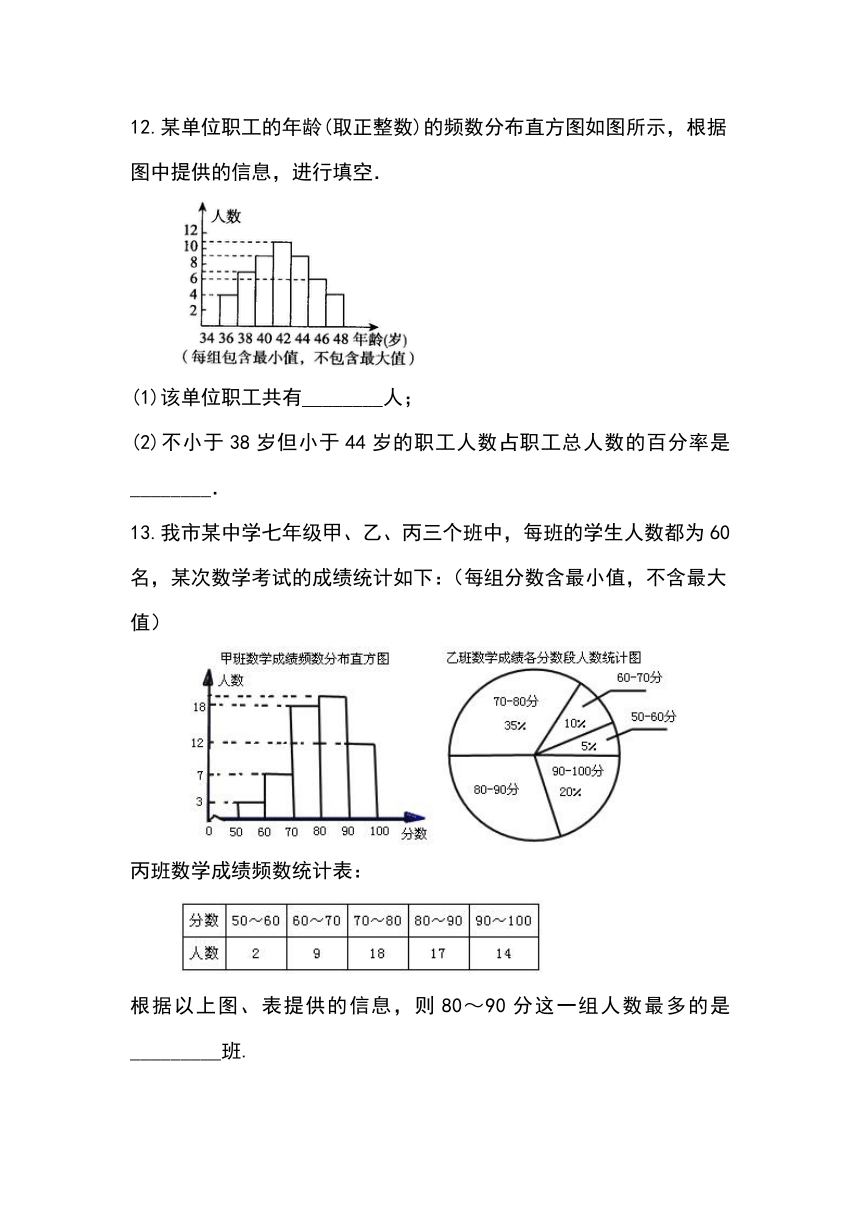
某单位职工的年龄(取正整数)的频数分布直方图如图所示,根据
图中提供的信息,进行填空.
(1)该单位职工共有________人;
(2)不小于38岁但小于44岁的职工人数占职工总人数的百分率是________.
13.我市某中学七年级甲、乙、丙三个班中,每班的学生人数都为60
名,某次数学考试的成绩统计如下:(每组分数含最小值,不含最大
值)
丙班数学成绩频数统计表:
根据以上图、表提供的信息,则80~90分这一组人数最多的是_________班.
14.某校为了解某个年级的学习情况,在这个年级抽取50名学生,对某学科进行测试,将所得成绩(成绩均为整数)整理后,列出表格:
分组
50~59分
60~69分
70~79分
80~89分
90~99分
频率
0.04
0.04
0.16
0.34
0.42
(1)本次测试90分以上的人数有________人;(包括90分)
(2)本次测试这50名学生成绩的及格率是________;(60分以上为及格,包括60分)
(3)这个年级此学科的学习情况如何?请在下列三个选项中,选一个填在题后的横线上________.
A.好
B.一般
C.不好
三、解答题
15.为了了解中学生的体能状况,某校抽取了50名学生进行1分钟
跳绳测试,将所得数据整理后,分成5组绘成了频数分布直方图,如
图(图中数据含最低值不含最高值).其中前4个小组的频率依次为
0.04,0.12,0.4,0.28.
(1)第4组的频数是多少?
(2)第5组的频率是多少?
(3)哪一组的频数最大?
(4)请补全频数分布直方图.
16.为检查某工厂所产8万台电扇的质量,抽查了其中40台,这40
台电扇的无故障连续使用时限如下:(单位:h)
248
256
232
243
188
278
286
292
308
312
274
296
288
302
295
208
314
290
281
298
228
287
217
329
283
327
272
264
307
257
268
278
266
289
312
198
204
254
244
278
(1)以组距20h列出样本的频数分布表,并画出频数分布直方图.
(2)估计8万台电扇中有多少台无故障连续使用时限会不少于288h?
(3)样本的平均无故障连续使用时限是多少?
(4)如果电扇的无故障正常(非连续)使用时限是无故障连续使用时限的8倍,那么这些电扇的正常使用寿命为多少小时?(精确到1h)
17.为了解某校九年级学生的身高情况,随机抽取部分学生的身高进行调查,利用所得数据绘成如图统计图表:
频数分布表
百分比
10%
20%
30%
12%
100%
频数
5
15
14
6
身高分组
总计
填空:=
,=
;
(2)补全频数分布直方图;
(3)该校九年级共有600名学生,估计身高不低于165cm的学生大约有多少人?
【答案与解析】
一、选择题
1.【答案】C;
【解析】频数直方图是按照数据从小到大的顺序排列,包括所有的
数据,即数据的变化范围是指数据的最大值和最小值的差.
2.【答案】A;
【解析】频数直方图中纵坐标表示的是频数,则小长方形的高为频
数,小长方形的面积=.
3.【答案】C;
【解析】解:∵数据的最大值为46,最小值为27,
∴这组数据的差是46﹣27=19,
∵组距为3,
∴这组数据应分成19÷3=6,则分成7组.
故选C.
4.【答案】B;
【解析】正确的是①③④.
5.【答案】B;
【解析】根据在频数直方图中,某一组相应的小长方形的面积与直
方图中所有小矩形面积的比值即这小组的频率,求得中间一个长方
形对应的频率后,再由频数、频率、总数的关系求解.
6.【答案】D;
【解析】解:根据题意身高157.5以上的频率为:
1-(0.017+0.050+0.100+0.133)=0.7,
因抽取了60名学生,则身高在157.5以上的学生有:60×0.7=42;故答案为D.
7.【答案】B;
【解析】.
8.【答案】D;
【解析】根据频率=计算.
二、填空题
9.【答案】8,4;
【解析】频数分布直方图中,各个长方形的高之比依次为3:2:4:
1,则指各组频数之比为3:2:4:1,据此即可求出第二小组的频数第四小组的频数.
10.【答案】53,47,5;
【解析】解:分析数据可得:最大的值是53,最小的值是47,则
它们的差为53﹣47=6;如果组距为1.5,由于=4;但由于要包
含两个端点,故可分为5组.
故本题答案为:53,47,5.
11.【答案】200;
【解析】解:∵E组的频率为:
1-0.04-0.08-0.16-0.36-0.12=0.24,
又∵E组的频数为48,
∴被调查的观众总人数为:48÷0.24=200.
故答案为200.
12.【答案】
(1)50
(2)58%
;
【解析】正确读图是解题的关键.
13.【答案】甲;
【解析】解:甲班:60-3-7-12-18=20(人)
乙班:60×(1-35%-10%-5%-20%)=18(人).
丙班:17(人).
所以最多的是甲班.
14.【答案】(1)21
;(2)96%
;(3)A.
【解析】(1)0.42×50=21.(2)1-0.04-0.96=96%.(3)理由是优秀率和及格率都很高.
三、解答题
15.【解析】
解:(1)第4组的频数是0.28×50=14.
(2)第5组频率为1-0.04-0.12-0.4-0.28=0.16.
(3)170~180这一组频数最大.
(4)补全如图:
16.【解析】
解:(1)频数分布表如下:
频数分布直方图如图:
(2)因为这40台中不少于288h的有9+5+1=15(台),
所以8万台电扇中不少于288h的有(万台).
(3)平均无故障连续使用时限为(h).
(4)电扇的正常寿命为271.3×8≈2170(h).
17.【解析】
解:(1)由表格可得,
调查的总人数为:5÷10%=50,
∴a=50×20%=10,
b=14÷50×100%=28%,
故答案为:10,28%;
(2)补全的频数分布直方图如下图所示,
(3)600×(28%+12%)=600×40%=240(人)
即该校九年级共有600名学生,身高不低于165cm的大约有240人.
【巩固练习】
一、选择题
1.为了绘出一批数据的频数分布直方图,首先计算出这批数据的变动范围是指数据的
(
)
A.最大值
B.最小值
C.最大值与最小值的差
D.个数
2.在频数分布直方图中,各小矩形的面积等于
(
)
A.相应各组的频数
B.组数
C.相应各组的频率
D.组距
3.已知一组数据的最大值为46,最小值为27,在绘制频数分布直方
图时,取组距为3,则这组数据应分成
( )
A.5组
B.6组
C.7组
D.8组
4.某班50名学生期末考试数学成绩的频数分布直方图如图所示,对图中提供的信息做出如下判断:
①成绩在50~60分段的人数与90~100分段的人数相等;
②从左到右数,第4小组的频率是0.03;
③成绩在80分以上的学生有20人;
④及格率为90%.
其中正确的判断有
(
)
A.4个
B.3个
C.2个
D.1个
5.在样本频数分布直方图中,有11个小长方形.若中间的小长方形
的面积等于其他10个小长方形面积之和的,且样本容量为160个,则中间的一组的频数为
(
)
A.0.2
B.32
C.0.25
D.40
6.
某学校随机抽取了同龄的60名学生,对其身高进行测量,测量数据(均为整数)进行整理后绘成频率分布直方图(如下图),图中自左向右各小组数据的频率依次为:0.017,0.050,0.100,0.133,0.300,0.183,0.167,0.050.则身高在157.5以上的学生有( )
A.18人
B.24人
C.39人
D.42人
7.有40个数据,其中最大值为35,最小值为15,若取组距为4,则应该分的组数是
(
)
A.4
B.5
C.6
D.7
学校为了解七年级学生参加课外兴趣小组活动情况,随机调查了
40名学生,将结果绘制成了如图所示的频数分布直方图,则参加绘画兴趣小组的频率是
(
)
A.0.1
B.0.15
C.0.25
D.0.3
二、填空题
9.已知样本容量是40,在样本的频数分布直方图中各小矩形的高之
比依次为3:2:4:1,则第二小组的频数为________,第四小组的频数
为________.
10.一个样本含有下面10个数据:52,51,49,50,47,48,50,51,48,53,则最大的值是
,最小的值是
,如果组距为1.5,则应分成
组.
11.为了解各年龄段观众对某电视节目的收视率,小明调查了部分观
众的收视情况,并分成A,B,C,D,E,F六组进行调查,其频率分
布直方图如图所示,各长方形上方的数据表示该组的频率,若E组的
频数为48,那么被调查的观众总人数为__________.
某单位职工的年龄(取正整数)的频数分布直方图如图所示,根据
图中提供的信息,进行填空.
(1)该单位职工共有________人;
(2)不小于38岁但小于44岁的职工人数占职工总人数的百分率是________.
13.我市某中学七年级甲、乙、丙三个班中,每班的学生人数都为60
名,某次数学考试的成绩统计如下:(每组分数含最小值,不含最大
值)
丙班数学成绩频数统计表:
根据以上图、表提供的信息,则80~90分这一组人数最多的是_________班.
14.某校为了解某个年级的学习情况,在这个年级抽取50名学生,对某学科进行测试,将所得成绩(成绩均为整数)整理后,列出表格:
分组
50~59分
60~69分
70~79分
80~89分
90~99分
频率
0.04
0.04
0.16
0.34
0.42
(1)本次测试90分以上的人数有________人;(包括90分)
(2)本次测试这50名学生成绩的及格率是________;(60分以上为及格,包括60分)
(3)这个年级此学科的学习情况如何?请在下列三个选项中,选一个填在题后的横线上________.
A.好
B.一般
C.不好
三、解答题
15.为了了解中学生的体能状况,某校抽取了50名学生进行1分钟
跳绳测试,将所得数据整理后,分成5组绘成了频数分布直方图,如
图(图中数据含最低值不含最高值).其中前4个小组的频率依次为
0.04,0.12,0.4,0.28.
(1)第4组的频数是多少?
(2)第5组的频率是多少?
(3)哪一组的频数最大?
(4)请补全频数分布直方图.
16.为检查某工厂所产8万台电扇的质量,抽查了其中40台,这40
台电扇的无故障连续使用时限如下:(单位:h)
248
256
232
243
188
278
286
292
308
312
274
296
288
302
295
208
314
290
281
298
228
287
217
329
283
327
272
264
307
257
268
278
266
289
312
198
204
254
244
278
(1)以组距20h列出样本的频数分布表,并画出频数分布直方图.
(2)估计8万台电扇中有多少台无故障连续使用时限会不少于288h?
(3)样本的平均无故障连续使用时限是多少?
(4)如果电扇的无故障正常(非连续)使用时限是无故障连续使用时限的8倍,那么这些电扇的正常使用寿命为多少小时?(精确到1h)
17.为了解某校九年级学生的身高情况,随机抽取部分学生的身高进行调查,利用所得数据绘成如图统计图表:
频数分布表
百分比
10%
20%
30%
12%
100%
频数
5
15
14
6
身高分组
总计
填空:=
,=
;
(2)补全频数分布直方图;
(3)该校九年级共有600名学生,估计身高不低于165cm的学生大约有多少人?
【答案与解析】
一、选择题
1.【答案】C;
【解析】频数直方图是按照数据从小到大的顺序排列,包括所有的
数据,即数据的变化范围是指数据的最大值和最小值的差.
2.【答案】A;
【解析】频数直方图中纵坐标表示的是频数,则小长方形的高为频
数,小长方形的面积=.
3.【答案】C;
【解析】解:∵数据的最大值为46,最小值为27,
∴这组数据的差是46﹣27=19,
∵组距为3,
∴这组数据应分成19÷3=6,则分成7组.
故选C.
4.【答案】B;
【解析】正确的是①③④.
5.【答案】B;
【解析】根据在频数直方图中,某一组相应的小长方形的面积与直
方图中所有小矩形面积的比值即这小组的频率,求得中间一个长方
形对应的频率后,再由频数、频率、总数的关系求解.
6.【答案】D;
【解析】解:根据题意身高157.5以上的频率为:
1-(0.017+0.050+0.100+0.133)=0.7,
因抽取了60名学生,则身高在157.5以上的学生有:60×0.7=42;故答案为D.
7.【答案】B;
【解析】.
8.【答案】D;
【解析】根据频率=计算.
二、填空题
9.【答案】8,4;
【解析】频数分布直方图中,各个长方形的高之比依次为3:2:4:
1,则指各组频数之比为3:2:4:1,据此即可求出第二小组的频数第四小组的频数.
10.【答案】53,47,5;
【解析】解:分析数据可得:最大的值是53,最小的值是47,则
它们的差为53﹣47=6;如果组距为1.5,由于=4;但由于要包
含两个端点,故可分为5组.
故本题答案为:53,47,5.
11.【答案】200;
【解析】解:∵E组的频率为:
1-0.04-0.08-0.16-0.36-0.12=0.24,
又∵E组的频数为48,
∴被调查的观众总人数为:48÷0.24=200.
故答案为200.
12.【答案】
(1)50
(2)58%
;
【解析】正确读图是解题的关键.
13.【答案】甲;
【解析】解:甲班:60-3-7-12-18=20(人)
乙班:60×(1-35%-10%-5%-20%)=18(人).
丙班:17(人).
所以最多的是甲班.
14.【答案】(1)21
;(2)96%
;(3)A.
【解析】(1)0.42×50=21.(2)1-0.04-0.96=96%.(3)理由是优秀率和及格率都很高.
三、解答题
15.【解析】
解:(1)第4组的频数是0.28×50=14.
(2)第5组频率为1-0.04-0.12-0.4-0.28=0.16.
(3)170~180这一组频数最大.
(4)补全如图:
16.【解析】
解:(1)频数分布表如下:
频数分布直方图如图:
(2)因为这40台中不少于288h的有9+5+1=15(台),
所以8万台电扇中不少于288h的有(万台).
(3)平均无故障连续使用时限为(h).
(4)电扇的正常寿命为271.3×8≈2170(h).
17.【解析】
解:(1)由表格可得,
调查的总人数为:5÷10%=50,
∴a=50×20%=10,
b=14÷50×100%=28%,
故答案为:10,28%;
(2)补全的频数分布直方图如下图所示,
(3)600×(28%+12%)=600×40%=240(人)
即该校九年级共有600名学生,身高不低于165cm的大约有240人.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
