苏科版九年级数学下册 7.6锐角三角函数全章巩固练习(含答案)
文档属性
| 名称 | 苏科版九年级数学下册 7.6锐角三角函数全章巩固练习(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 389.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-29 00:00:00 | ||
图片预览





文档简介
《锐角三角函数》全章复习与巩固--巩固练习(基础)
选择题
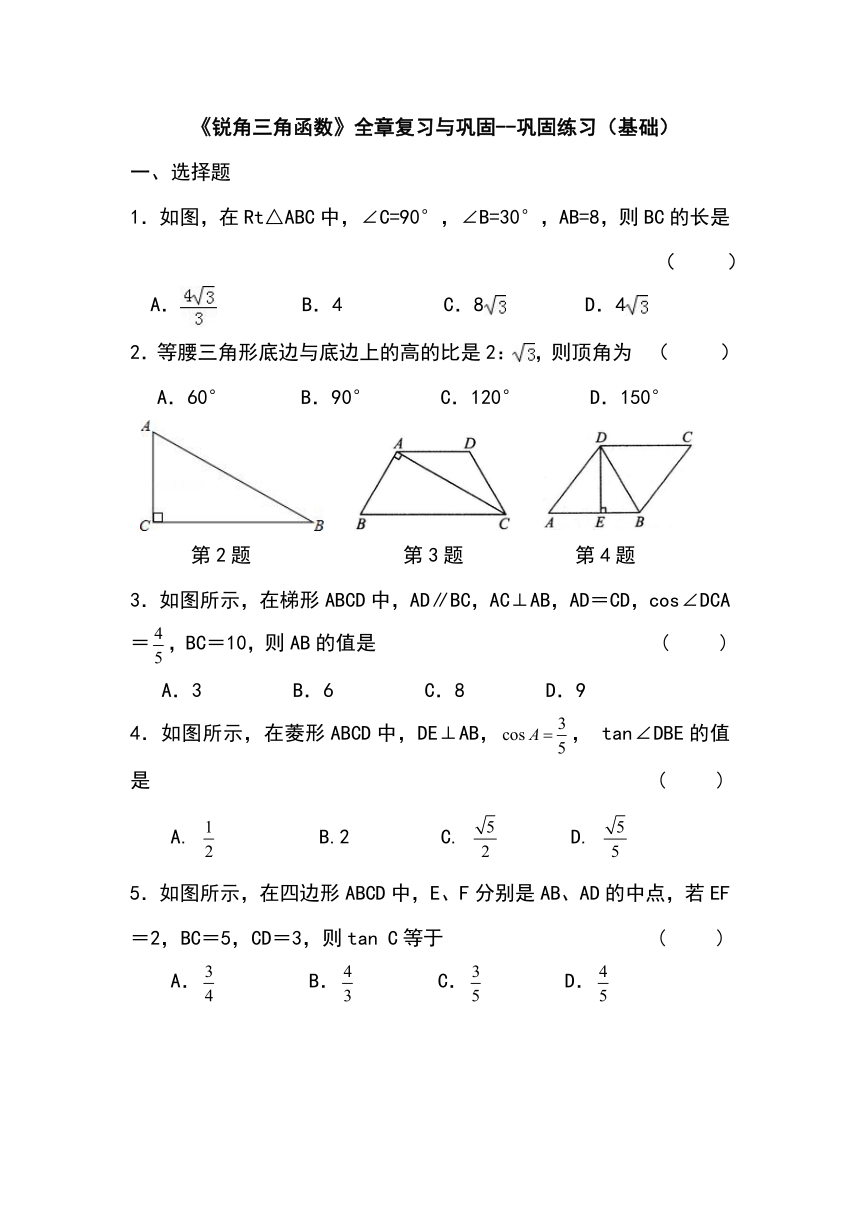
1.如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=8,则BC的长是
(
)
A.
B.4
C.8
D.4
2.等腰三角形底边与底边上的高的比是2:,则顶角为
(
)
A.60°
B.90°
C.120°
D.150°
第2题
第3题
第4题
3.如图所示,在梯形ABCD中,AD∥BC,AC⊥AB,AD=CD,cos∠DCA=,BC=10,则AB的值是
(
)
A.3
B.6
C.8
D.9
4.如图所示,在菱形ABCD中,DE⊥AB,,
tan∠DBE的值是
(
)
A.
B.2
C.
D.
5.如图所示,在四边形ABCD中,E、F分别是AB、AD的中点,若EF=2,BC=5,CD=3,则tan
C等于
(
)
A.
B.
C.
D.
第5题图
第7题图
6.已知Rt△ABC中,∠C=90°,,则cosA的值为(
)
A.
B.
C.
D.
7.如图所示,先锋村准备在坡角为α的山坡上栽树,要求相邻两树
之间的水平距离为5米,那么这两树在坡面上的距离AB为
(
)
A.5cosα米
B.米
C.米
D.米
8.等腰三角形一腰上的高与腰长之比是1:2,则等腰三角形顶角的度数为
(
)
A.30°
B.50°
C.60°或120°
D.30°或150°
二、填空题
9.计算:________.
10.如图所示,已知Rt△ABC中,斜边BC上的高AD=4,,则AC=________.
11.如图所示,将以A为直角顶点的等腰直角三角形ABC沿直线BC
平移得到,使点与C重合,连接,则tan∠的值____.
第10题图
第11题图
第12题图
12.如图所示,一架梯子斜靠在墙上,若梯子底端到墙的距离AC=3米,,则梯子长AB=_______米.
13.如图所示,已知正方形ABCD的边长为2,如果将线段BD绕着点B
旋转后,点D落在CB的延长线上的
处,那么tan∠BAD′等于_____.
第13题
第15题
第16题
14.一次函数经过(tan
45°,tan
60°)和(-cos
60°,-6tan30°),则此一次函数的解析式为________.
15.如图所示,在△ABC中,∠ACB=90°,CD是AB边的中线,AC=6,CD=5,则sinA等于________.
16.如图,在边长相同的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB,CD相交于点P,则的值= ,tan∠APD的值= .
三、解答题
17.如图是某市一座人行过街天桥,天桥高CB=5米,斜坡AC的坡度为1:1,为了方便行人推车过天桥,市政部门决定降低坡度,使新
坡面的傾斜角为30°.若新坡脚前需留3m的人行道,问离原坡脚A处7m的建筑物M是否需要拆除,请说明理由.
(≈1.73)
18.如图所示,在梯形ABCD中,AD∥BC,AB=DC=8,∠B=60°,BC=12,连接AC.
(1)求tan∠ACB的值;
(2)若M、N分别是AB、DC的中点,连接MN,求线段MN的长.
19.如图所示,点E、C在BF上,BE=FC,∠ABC=∠DEF=45°,∠A=∠D=90°.
(1)求证:AB=DE;
(2)若AC交DE于M,且AB=,ME=,将线段CE绕点C顺时针旋转,使点E旋转到AB上的G处,求旋转角∠ECG的度数.
如图所示,AB是⊙O的直径,点C在BA的延长线上,直线CD与
⊙O相切于点D,弦DF⊥AB于点E,线段CD=10,连接BD.
(1)求证:∠CDE=2∠B;
(2)若BD:AB=:2,求⊙O的半径及DF的长.
一、选择题
1.【答案】D.
【解析】∵在Rt△ABC中,∠C=90°,∠B=30°,AB=8,cosB=,即cos30°=,
∴BC=8×=4;故选:D.
2.【答案】A;
【解析】如图,在△ABC中,AB=AC,AD⊥CB于D,
依题意得CD:AD=1:=:3,
而tan∠DAC=CD:AD,
∴tan∠DAC=:3,
∴∠DAC=30°,
∴顶角∠BAC=60°.
3.【答案】B;
【解析】因为AD=DC,所以∠DAC=∠DCA,
又∵
AD∥BC,∴
∠DAC=∠ACB,
所以∠DCA=∠ACB.在Rt△ACB中,AC=BC·cos∠BCA=,则.
4.【答案】B;
【解析】∵
DE⊥AB,∴
在Rt△ADE中,cosA=.
∴
设AD=5,则AE=3,DE=4,又AD=AB,
∴
BE=2,
∴
tan∠DBE=.
5.【答案】B;
【解析】如图所示,连结BD,
由三角形中位线定理得
BD=2EF=2×2=4,又BC=5,CD=3,
∴
CD2+BD2=BC2.
∴
△BDC是直角三角形.且∠BDC=90°,
∴
.
6.【答案】C;
【解析】∵
,
∴
∠B=60°,∠A=90°-60°=30°,
∴
.
7.【答案】B;
【解析】由上图知,
在Rt△ABC中,.
∴.
8.【答案】D;
【解析】有两种情况:
当∠A为锐角时,如图(1),sin
A=,∠A=30°;
当∠A为钝角时,如图(2),sin(180°-∠BAC)=,
180°-∠BAC=30°,∠BAC=150°.
二、填空题
9.【答案】;
【解析】原式=.
10.【答案】5;
【解析】在Rt△ABC中,.AD⊥BC,所以∠CAD=∠B.
∴
,∴
,
又∵
AD=4,
∴
AC=5..
11.【答案】;
【解析】过作于点D,
在Rt△中,设,
则,BC=2x,BD=3x.
12.【答案】4
;
【解析】由,知,AB=4米.
13.【答案】;
【解析】由题意知.
在Rt△ABD′中,.
14.【答案】;
【解析】tan
45°=1,
tan60°=,
-cos60°=,
-6tan30°=.
设经过点、,
则用待定系数法可求出,.
15.【答案】;
【解析】∵
CD是Rt△ABC斜边上的中线,
∴
AB=2CD=2×5=10,BC=,
∴
.
16.【答案】3,2.
【解析】解:∵
四边形BCED是正方形,
∴
DB∥AC,
∴
△DBP∽△CAP,∴
==3,
连接BE,
∵
四边形BCED是正方形,
∴
DF=CF=CD,BF=BE,CD=BE,BE⊥CD,
∴
BF=CF,
根据题意得:AC∥BD,
∴
△ACP∽△BDP,
∴
DP:CP=BD:AC=1:3,
∴
DP:DF=1:2,
∴
DP=PF=CF=BF,
在Rt△PBF中,tan∠BPF==2,
∵
∠APD=∠BPF,∴
tan∠APD=2,
三、解答题
17.【答案与解析】
解:在Rt△ABC中,∠ABC=90°,BC=5,
∵
i=1:1,
∴
AB=5,
在Rt△DBC中,∠DBC=90°,∠CDB=30°,BC=5,
tan30°=,
∴
=,
解得DB==5×1.73≈8.65,
∵
BM=7+5=12,BD≈8.65,
∴
12﹣8.65>3,
所以,离原坡脚7m的建筑物无需拆除.
18.【答案与解析】
(1)如图所示,作AE⊥BC于E,
则BE=AB·cos
B=8cos
60°=.
AE=AB·sin
B=8sin
60°=.
∴
EC=BC-BE=12—4=8.
∴
在Rt△ACE中,tan∠ACB=
(2)作DF⊥BC于F,则AE∥DF,
∵
AD∥EF,∴
四边形AEFD是矩形.AD=EF.
∵
AB=DC,∴
∠B=∠DCF.
又∵∠AEB=∠DFC=90°,∴
△ABE△≌△DCF(AAS).
∴
FC=BE=4,∴
EF=BC-BE—FC=4.∴
AD=4.
∴
MN=(AD+BC)=×(4+12)=8.
19.【答案与解析】
(1)证明:∵
BE=FC,∴
BC=EF.
又∵
∠ABC=∠DEF,∠A=∠D,
∴
△ABC≌△DEF.∴
AB=DE.
(2)解:∵
∠DEF=∠B=45°,∴
DE∥AB.
∴
∠CME=∠A=90°.
∴
AC=AB=,MC=ME=.∴
CG=CE=2.
在Rt△CAG中,,∴
∠ACG=30°.
∴
∠ECG=∠ACB-∠ACB=45°-30°=15°.
20.【答案与解析】
(1)连接OD,
∵
直线CD与⊙O相切于点D,
∴
OD⊥CD,∴
∠CD0=90°,
∴
∠CDE+∠ODE=90°.
又∵
DF⊥AB,
∴
∠DEO=∠DEC=90°,∴
∠EOD+∠ODE=90°.
∴
∠CDE=∠EOD.
又∵
∠EOD=2∠B;∴
∠CDE=2∠B.
(2)连接AD.∵
AB是⊙O的直径,
∴
∠ADB=90°.
∵
BD:AB=:2,
∴
在Rt△ADB中,,
∴
∠B=30°,
∵
∠AOD=2∠B=60°.
又∵
∠CDO=90°,
∴
∠C=30°,
∵
在Rt△CDO中,CD=10,
∴
OD=10tan
30°=.即⊙O的半径为.
在Rt△CDE中,CD=10,∠C=30°,
∴
DE=CDsin
30°=5.
∵
弦DF⊥直径AB于点E,
∴
DE=EF=DF,
∴
DF=2DE=10.
选择题
1.如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=8,则BC的长是
(
)
A.
B.4
C.8
D.4
2.等腰三角形底边与底边上的高的比是2:,则顶角为
(
)
A.60°
B.90°
C.120°
D.150°
第2题
第3题
第4题
3.如图所示,在梯形ABCD中,AD∥BC,AC⊥AB,AD=CD,cos∠DCA=,BC=10,则AB的值是
(
)
A.3
B.6
C.8
D.9
4.如图所示,在菱形ABCD中,DE⊥AB,,
tan∠DBE的值是
(
)
A.
B.2
C.
D.
5.如图所示,在四边形ABCD中,E、F分别是AB、AD的中点,若EF=2,BC=5,CD=3,则tan
C等于
(
)
A.
B.
C.
D.
第5题图
第7题图
6.已知Rt△ABC中,∠C=90°,,则cosA的值为(
)
A.
B.
C.
D.
7.如图所示,先锋村准备在坡角为α的山坡上栽树,要求相邻两树
之间的水平距离为5米,那么这两树在坡面上的距离AB为
(
)
A.5cosα米
B.米
C.米
D.米
8.等腰三角形一腰上的高与腰长之比是1:2,则等腰三角形顶角的度数为
(
)
A.30°
B.50°
C.60°或120°
D.30°或150°
二、填空题
9.计算:________.
10.如图所示,已知Rt△ABC中,斜边BC上的高AD=4,,则AC=________.
11.如图所示,将以A为直角顶点的等腰直角三角形ABC沿直线BC
平移得到,使点与C重合,连接,则tan∠的值____.
第10题图
第11题图
第12题图
12.如图所示,一架梯子斜靠在墙上,若梯子底端到墙的距离AC=3米,,则梯子长AB=_______米.
13.如图所示,已知正方形ABCD的边长为2,如果将线段BD绕着点B
旋转后,点D落在CB的延长线上的
处,那么tan∠BAD′等于_____.
第13题
第15题
第16题
14.一次函数经过(tan
45°,tan
60°)和(-cos
60°,-6tan30°),则此一次函数的解析式为________.
15.如图所示,在△ABC中,∠ACB=90°,CD是AB边的中线,AC=6,CD=5,则sinA等于________.
16.如图,在边长相同的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB,CD相交于点P,则的值= ,tan∠APD的值= .
三、解答题
17.如图是某市一座人行过街天桥,天桥高CB=5米,斜坡AC的坡度为1:1,为了方便行人推车过天桥,市政部门决定降低坡度,使新
坡面的傾斜角为30°.若新坡脚前需留3m的人行道,问离原坡脚A处7m的建筑物M是否需要拆除,请说明理由.
(≈1.73)
18.如图所示,在梯形ABCD中,AD∥BC,AB=DC=8,∠B=60°,BC=12,连接AC.
(1)求tan∠ACB的值;
(2)若M、N分别是AB、DC的中点,连接MN,求线段MN的长.
19.如图所示,点E、C在BF上,BE=FC,∠ABC=∠DEF=45°,∠A=∠D=90°.
(1)求证:AB=DE;
(2)若AC交DE于M,且AB=,ME=,将线段CE绕点C顺时针旋转,使点E旋转到AB上的G处,求旋转角∠ECG的度数.
如图所示,AB是⊙O的直径,点C在BA的延长线上,直线CD与
⊙O相切于点D,弦DF⊥AB于点E,线段CD=10,连接BD.
(1)求证:∠CDE=2∠B;
(2)若BD:AB=:2,求⊙O的半径及DF的长.
一、选择题
1.【答案】D.
【解析】∵在Rt△ABC中,∠C=90°,∠B=30°,AB=8,cosB=,即cos30°=,
∴BC=8×=4;故选:D.
2.【答案】A;
【解析】如图,在△ABC中,AB=AC,AD⊥CB于D,
依题意得CD:AD=1:=:3,
而tan∠DAC=CD:AD,
∴tan∠DAC=:3,
∴∠DAC=30°,
∴顶角∠BAC=60°.
3.【答案】B;
【解析】因为AD=DC,所以∠DAC=∠DCA,
又∵
AD∥BC,∴
∠DAC=∠ACB,
所以∠DCA=∠ACB.在Rt△ACB中,AC=BC·cos∠BCA=,则.
4.【答案】B;
【解析】∵
DE⊥AB,∴
在Rt△ADE中,cosA=.
∴
设AD=5,则AE=3,DE=4,又AD=AB,
∴
BE=2,
∴
tan∠DBE=.
5.【答案】B;
【解析】如图所示,连结BD,
由三角形中位线定理得
BD=2EF=2×2=4,又BC=5,CD=3,
∴
CD2+BD2=BC2.
∴
△BDC是直角三角形.且∠BDC=90°,
∴
.
6.【答案】C;
【解析】∵
,
∴
∠B=60°,∠A=90°-60°=30°,
∴
.
7.【答案】B;
【解析】由上图知,
在Rt△ABC中,.
∴.
8.【答案】D;
【解析】有两种情况:
当∠A为锐角时,如图(1),sin
A=,∠A=30°;
当∠A为钝角时,如图(2),sin(180°-∠BAC)=,
180°-∠BAC=30°,∠BAC=150°.
二、填空题
9.【答案】;
【解析】原式=.
10.【答案】5;
【解析】在Rt△ABC中,.AD⊥BC,所以∠CAD=∠B.
∴
,∴
,
又∵
AD=4,
∴
AC=5..
11.【答案】;
【解析】过作于点D,
在Rt△中,设,
则,BC=2x,BD=3x.
12.【答案】4
;
【解析】由,知,AB=4米.
13.【答案】;
【解析】由题意知.
在Rt△ABD′中,.
14.【答案】;
【解析】tan
45°=1,
tan60°=,
-cos60°=,
-6tan30°=.
设经过点、,
则用待定系数法可求出,.
15.【答案】;
【解析】∵
CD是Rt△ABC斜边上的中线,
∴
AB=2CD=2×5=10,BC=,
∴
.
16.【答案】3,2.
【解析】解:∵
四边形BCED是正方形,
∴
DB∥AC,
∴
△DBP∽△CAP,∴
==3,
连接BE,
∵
四边形BCED是正方形,
∴
DF=CF=CD,BF=BE,CD=BE,BE⊥CD,
∴
BF=CF,
根据题意得:AC∥BD,
∴
△ACP∽△BDP,
∴
DP:CP=BD:AC=1:3,
∴
DP:DF=1:2,
∴
DP=PF=CF=BF,
在Rt△PBF中,tan∠BPF==2,
∵
∠APD=∠BPF,∴
tan∠APD=2,
三、解答题
17.【答案与解析】
解:在Rt△ABC中,∠ABC=90°,BC=5,
∵
i=1:1,
∴
AB=5,
在Rt△DBC中,∠DBC=90°,∠CDB=30°,BC=5,
tan30°=,
∴
=,
解得DB==5×1.73≈8.65,
∵
BM=7+5=12,BD≈8.65,
∴
12﹣8.65>3,
所以,离原坡脚7m的建筑物无需拆除.
18.【答案与解析】
(1)如图所示,作AE⊥BC于E,
则BE=AB·cos
B=8cos
60°=.
AE=AB·sin
B=8sin
60°=.
∴
EC=BC-BE=12—4=8.
∴
在Rt△ACE中,tan∠ACB=
(2)作DF⊥BC于F,则AE∥DF,
∵
AD∥EF,∴
四边形AEFD是矩形.AD=EF.
∵
AB=DC,∴
∠B=∠DCF.
又∵∠AEB=∠DFC=90°,∴
△ABE△≌△DCF(AAS).
∴
FC=BE=4,∴
EF=BC-BE—FC=4.∴
AD=4.
∴
MN=(AD+BC)=×(4+12)=8.
19.【答案与解析】
(1)证明:∵
BE=FC,∴
BC=EF.
又∵
∠ABC=∠DEF,∠A=∠D,
∴
△ABC≌△DEF.∴
AB=DE.
(2)解:∵
∠DEF=∠B=45°,∴
DE∥AB.
∴
∠CME=∠A=90°.
∴
AC=AB=,MC=ME=.∴
CG=CE=2.
在Rt△CAG中,,∴
∠ACG=30°.
∴
∠ECG=∠ACB-∠ACB=45°-30°=15°.
20.【答案与解析】
(1)连接OD,
∵
直线CD与⊙O相切于点D,
∴
OD⊥CD,∴
∠CD0=90°,
∴
∠CDE+∠ODE=90°.
又∵
DF⊥AB,
∴
∠DEO=∠DEC=90°,∴
∠EOD+∠ODE=90°.
∴
∠CDE=∠EOD.
又∵
∠EOD=2∠B;∴
∠CDE=2∠B.
(2)连接AD.∵
AB是⊙O的直径,
∴
∠ADB=90°.
∵
BD:AB=:2,
∴
在Rt△ADB中,,
∴
∠B=30°,
∵
∠AOD=2∠B=60°.
又∵
∠CDO=90°,
∴
∠C=30°,
∵
在Rt△CDO中,CD=10,
∴
OD=10tan
30°=.即⊙O的半径为.
在Rt△CDE中,CD=10,∠C=30°,
∴
DE=CDsin
30°=5.
∵
弦DF⊥直径AB于点E,
∴
DE=EF=DF,
∴
DF=2DE=10.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
