人教版七年级数学下册 7.1.2平面直角坐标系课件(共36张PPT)
文档属性
| 名称 | 人教版七年级数学下册 7.1.2平面直角坐标系课件(共36张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 959.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-29 15:01:00 | ||
图片预览



文档简介
(共36张PPT)
7.1
平面直角坐标系
第七章
平面直角坐标系
7.1.2
平面直角坐标系
1.理解并能画出平面直角坐标系;
2.
能写出坐标系内点的坐标;
3.能根据点的坐标把点描到坐标系内;
4.掌握x轴和y轴上点的坐标特征。
学习目标(一)
自学指导
自学课本66页内容,思考:
1、回忆:实数与数轴上的点存在什么关系?
2、要确定平面内的一个点,需要怎样表示呢?
3、什么是平面直角坐标系?它由哪些元素构成?
4、用平面直角坐标系表示点时,数对按怎样顺序表示?
5、原点O的坐标是什么?X轴和y轴上的点的坐标有什么特征?
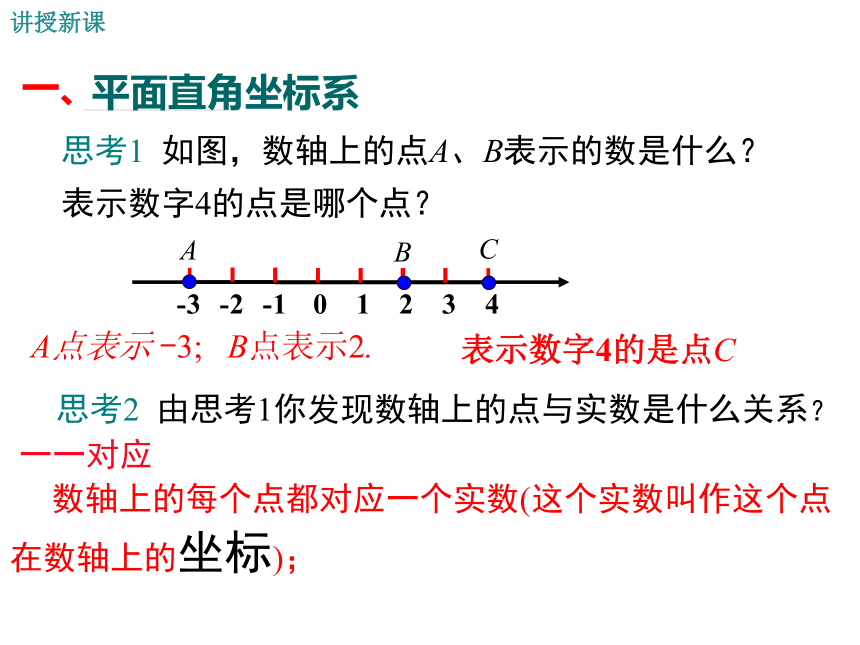
思考1
如图,数轴上的点A、B表示的数是什么?
表示数字4的点是哪个点?
思考2
由思考1你发现数轴上的点与实数是什么关系?
一一对应
数轴上的每个点都对应一个实数(这个实数叫作这个点在数轴上的坐标);
A点表示
-3;
B点表示2.
表示数字4的是点C
讲授新课
一、
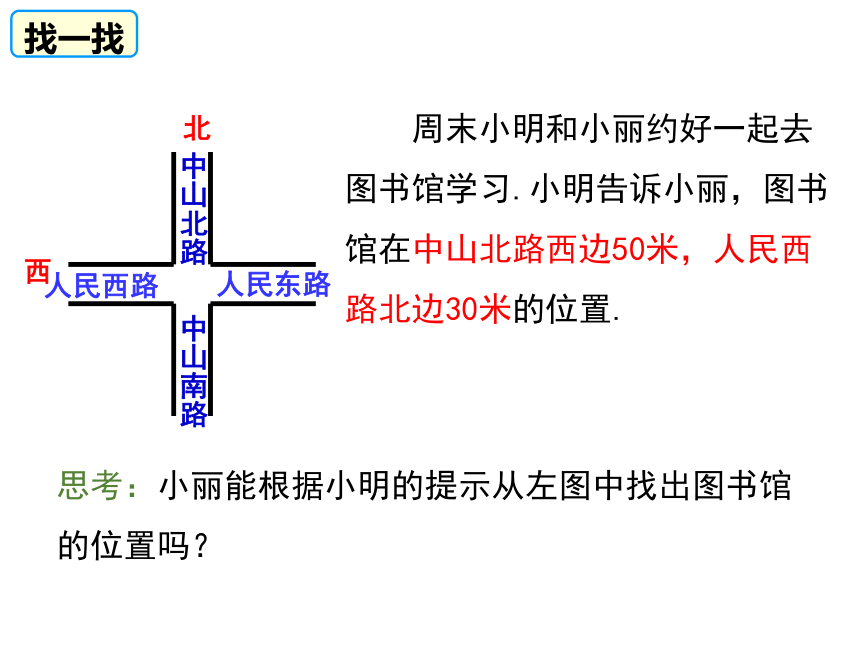
思考:小丽能根据小明的提示从左图中找出图书馆的位置吗?
周末小明和小丽约好一起去图书馆学习.小明告诉小丽,图书馆在中山北路西边50米,人民西路北边30米的位置.
找一找
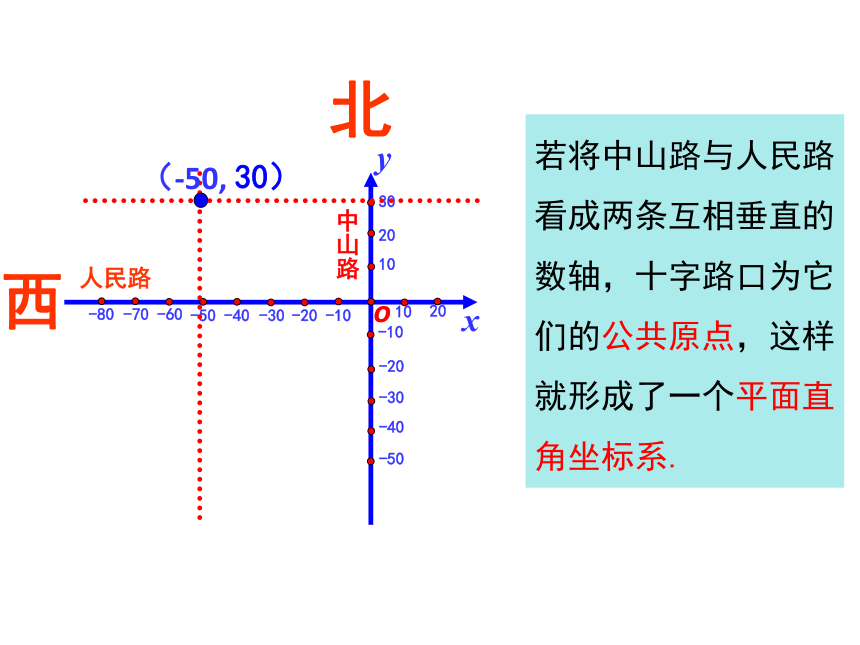
若将中山路与人民路看成两条互相垂直的数轴,十字路口为它们的公共原点,这样就形成了一个平面直角坐标系.
x
y
o
30
20
10
20
10
-10
-20
-30
-40
-20
-50
-10
-70
-60
-50
-40
-30
-80
(-50,
北
西
30)
人民路
中山路
O
y
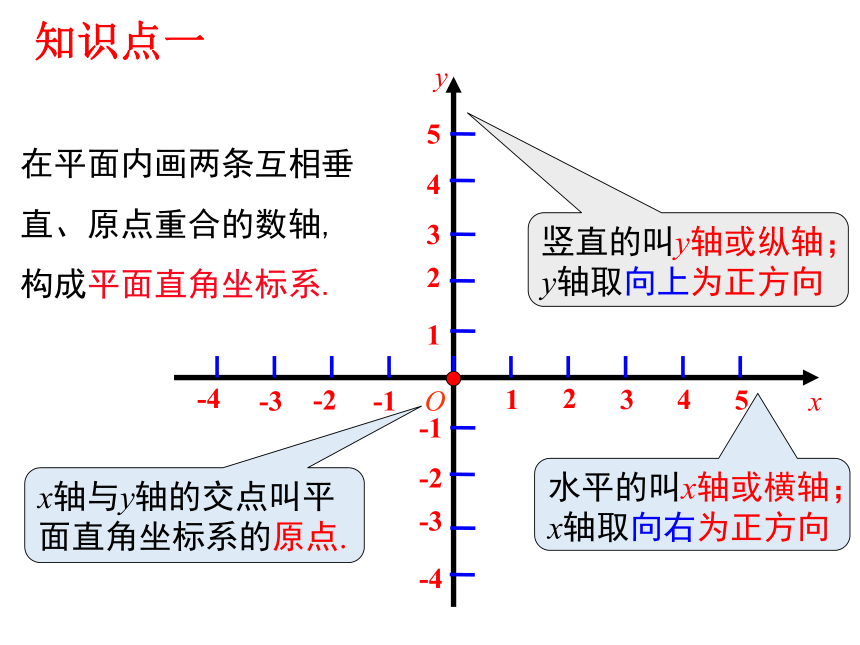
在平面内画两条互相垂直、原点重合的数轴,构成平面直角坐标系.
1
2
3
4
5
-4
-3
-2
-1
x
竖直的叫y轴或纵轴;
y轴取向上为正方向
水平的叫x轴或横轴;
x轴取向右为正方向
x轴与y轴的交点叫平面直角坐标系的原点.
知识点一
x
O
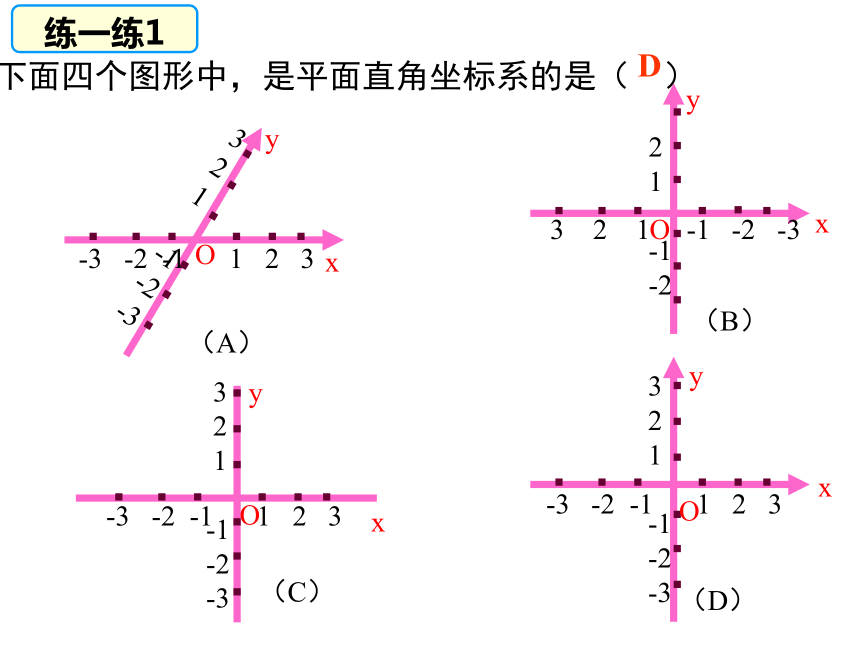
下面四个图形中,是平面直角坐标系的是(
)
x
x
y
(A)
3
2
1
-1
-2
-3
x
y
(B)
2
1
-1
-2
O
D
练一练1
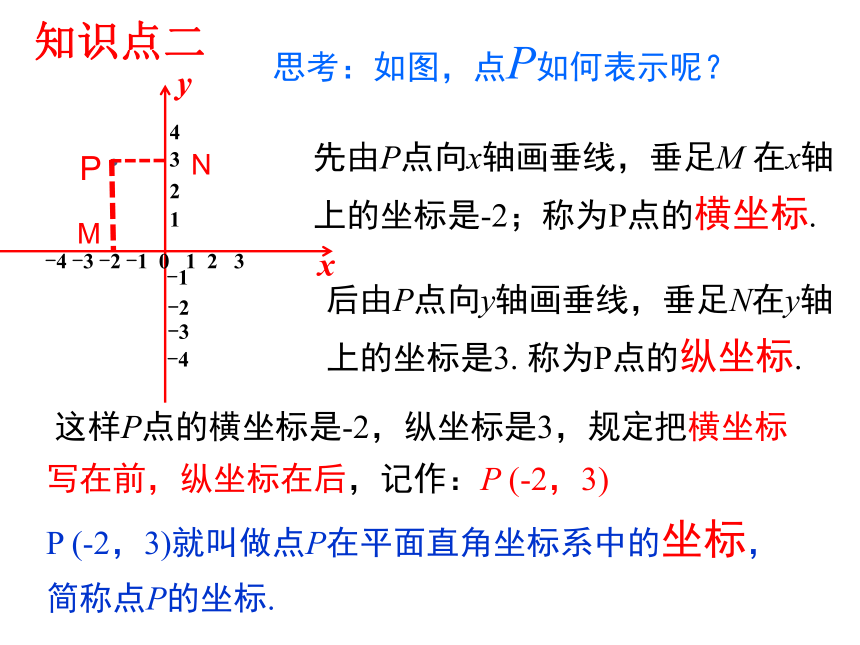
这样P点的横坐标是-2,纵坐标是3,规定把横坐标写在前,纵坐标在后,记作:P
(-2,3)
P
(-2,3)就叫做点P在平面直角坐标系中的坐标,简称点P的坐标.
思考:如图,点P如何表示呢?
后由P点向y轴画垂线,垂足N在y轴上的坐标是3.
称为P点的纵坐标.
先由P点向x轴画垂线,垂足M
在x轴上的坐标是-2;称为P点的横坐标.
P
N
M
知识点二
1
1
-1
-2
-3
-4
2
3
2
3
4
5
4
-1
-2
-3
-4
-5
o
A
(4,3)
x
y
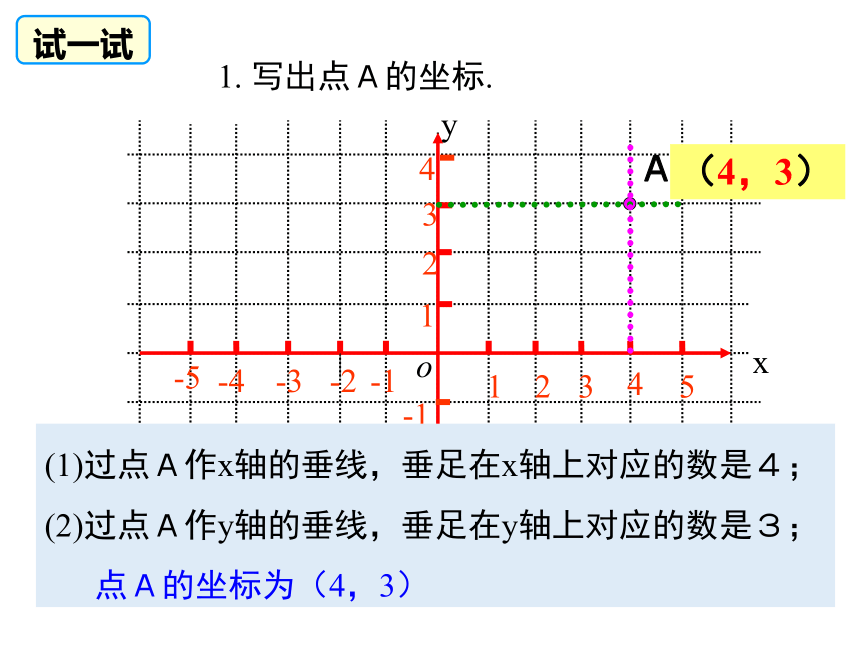
1.
写出点A的坐标.
(1)过点A作x轴的垂线,垂足在x轴上对应的数是4;
(2)过点A作y轴的垂线,垂足在y轴上对应的数是3;
点A的坐标为(4,3)
试一试
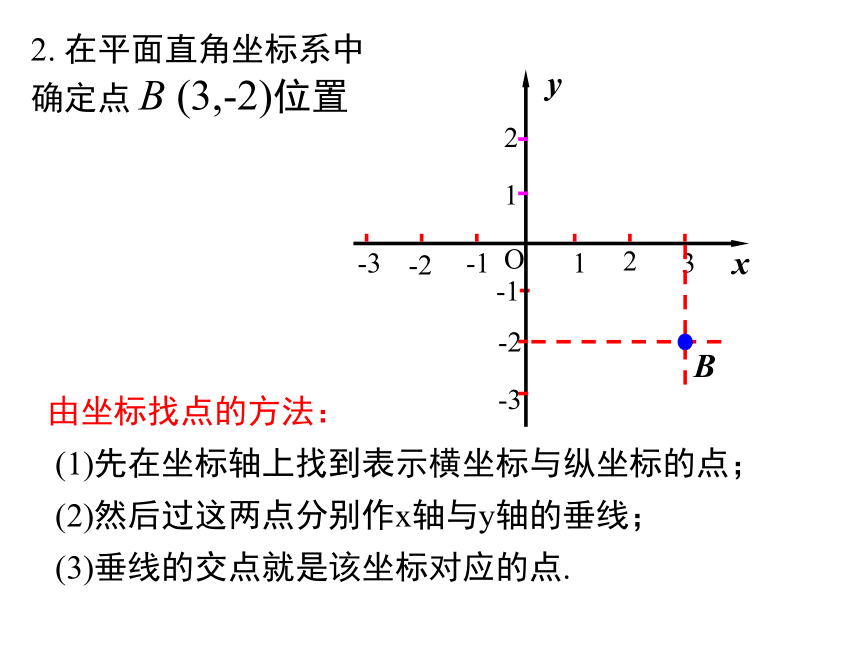
2.
在平面直角坐标系中
确定点
B
(3,-2)位置
由坐标找点的方法:
(1)先在坐标轴上找到表示横坐标与纵坐标的点;
(2)然后过这两点分别作x轴与y轴的垂线;
(3)垂线的交点就是该坐标对应的点.
B
A
B
C
E
F
D
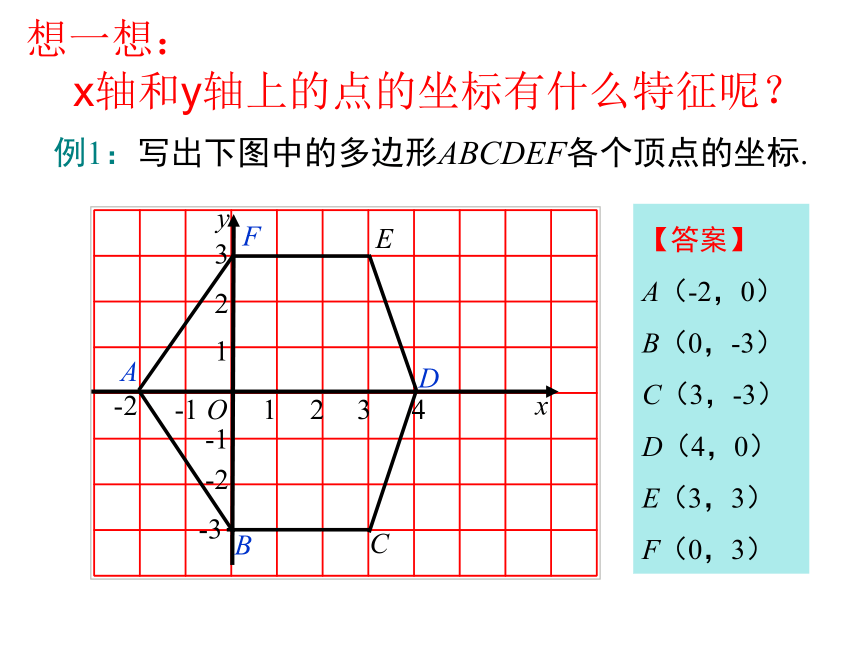
例1:写出下图中的多边形ABCDEF各个顶点的坐标.
1
2
3
4
-1
-2
1
2
3
-1
-2
-3
【答案】
A(-2,0)
B(0,-3)
C(3,-3)
D(4,0)
E(3,3)
F(0,3)
y
O
x
想一想:
x轴和y轴上的点的坐标有什么特征呢?
在直角坐标系中描下列各点:
A(4,3),
B(-2,3),
C(-4,-1),
D(2,-2),
E(0,4)
x
y
练一练2
·
E
学习目标(二)
1.理解“象限”的概念并掌握各象限的位置;
2.掌握各象限内点的坐标符号特征;
3.能根据横、纵坐标的符号确定点的位置.
4.能根据实际情况建立不同的坐标系解决问题。
阅读课本67页—68页内容,思考:
1、什么是“象限”?象限是怎样划分的?
2、想一想,每个象限内点的坐标在符号上有什么特征?
3、数轴上的点与实数一一对应,那么平面内的点和谁有对应关系呢?
4、合作交流,完成68页“探究”
自学指导
在平面直角坐标系中,两条坐标轴(即横轴和纵轴)把平面分成如图所示的Ⅰ,Ⅱ
,Ⅲ,Ⅳ四个区域.
分别称为第一,二,三,四象限.
注意:坐标轴上的点不属于任何一个象限.
活动1:
观察坐标系,填写各象限内的点的坐标的特征:
+
+
+
-
-
-
+
-
交流:不看平面直角坐标系,你能迅速说出A(4,5)
,
B(-2,3),
C(-4,-1),
D(2.5,-2),
E(0,-4)所在的象限吗?
知识点三
点的位置
横坐标的符号
纵坐标的
符号
第一象限
第二象限
第三象限
第四象限
0
+
+
-
-
0
0
0
交流:不看平面直角坐标系,你能迅速说A(4,0),
B(0,3),C(-4,0),E(0,-4),O(0,0)所在的位置吗?
想一想:
观察坐标系,填写坐标轴上的点的坐标的特征:
点的位置
横坐标的符号
纵坐标的符号
在x轴的正半轴上
在x轴的负半轴上
在y轴的正半轴上
在y轴的负半轴上
例2:在平面直角坐标系中,描出下列各点,并说出它们分别在哪个象限.
A(5,4),B(-3,4),C
(-4
,-1),
D(2,-4).
问题.
坐标平面内的点与有序数对(坐标)是什么关系?
类似“数轴上的点与实数一一对应”
我们可以得出:
坐标平面内的点与有序数对是一一对应的.
完成课本70页第5题
练一练3
建立坐标系求图形中点的坐标
问题:正方形ABCD的边长为4,请建立一个平面直角坐标系,并写出正方形的四个顶点A,B,C,D在这个平面直角坐标系中的坐标.
A
B
C
D
三、
(O)
x
y
解:如图,正方形四个顶点A,B,C,D的坐标分别为:
A(0,0),
B(4,0),
C(4,4),
D(0,4).
A
B
C
D
A(0,-4),
B(4,-4),C(4,0),
D(0,0).
想一想:还可以建立其他平面直角坐标系,表示正方形的四个顶点A,B,C,D的坐标吗?
A(-4,0),
B(0,0),C(0,4),
D(-4,4).
A(-4,-4),
B(0,-4),C(0,0),
D(-4,0).
A(-2,-2),
B(2,-2),C(2,2),
D(-2,2).
由上得知,建立的平面直角坐标系不同,则各点的坐标也不同.
【总结】
建立平面直角坐标系,一般要使图形上的点的坐标便于确定。
需要说明的是,虽然建立不同的平面直角坐标系,同一个点会有不同的坐标,但正方形的形状和性质不会改变.
知识点四
例3:长方形的两条边长分别为4,6,建立适当的直角坐标系,使它的一个顶点的坐标为(-2,-3).请你写出另外三个顶点的坐标.
解:如图,
建立直角坐标系,
∵长方形的一个顶点的坐标为A(-2,-3),
∴长方形的另外三个顶点的坐标分别为
B(2,-3),
C(2,3),D(-2,3).
右图是一个围棋棋盘(局部),把这个围棋棋盘放置在一个平面直角坐标系中,白棋①的坐标是(-2,-1),白棋③的坐标是(-1,-3),则黑棋?的坐标是_______.
练一练4
(1,-2)
y
x
O
当堂练习
1.如图,点A的坐标为(
)
A.
(
-2,3)
B.
(
2,-3)
C
.
(
-2,-3)
D
.
(
2,3)
x
y
O
1
2
3
-3
-2
-1
1
2
-1
-2
A
A
2.如图,点A的坐标为
,
点B的坐标为
.
x
y
O
1
2
3
-3
-2
-1
1
2
-1
-2
A
B
(-2,0)
(0,-2)
3.在
y轴上的点的横坐标是______,
在
x轴上的点的纵坐标是
______.
4.点
M(-
8,12)到
x轴的距离是_______,
到
y轴的距离是
_________
.
0
0
12
8
A(3,6)
B(0,-8)
C(-7,-5)
D(-6,0)
E(-3.6,5)
F(5,-6)
G(0,0)
第一象限
第三象限
第二象限
第四象限
y
轴负半轴
x
轴负半轴
原点
5.下列各点分别在坐标平面的什么位置上?
平面直角坐标系及点的坐标
定义:原点、坐标轴
课堂小结
点的坐标
定义与符号特征
点的坐标的确定
建立合适的平面直角坐标系
课堂作业:
课本70页,第7题。
例4
设点M(a,b)为平面直角坐标系内的点.
(1)当a>0,b<0时,点M位于第几象限?
(2)当ab>0时,点M位于第几象限?
(3)当a为任意有理数,且b<0时,点M位于第几象限?
解:(1)点M在第四象限;
(2)在第一象限(a>0,b>0)或者在第三象限(a<0,b<0);
(3)在第三象限(a<0,b<0)或者第四象限(a>0,b<0)或者在y轴上(a=0,b<0).
延伸拓展
练一练
已在平面直角坐标系中,点P(3,m-2)在第一象限内,则m的取值范围是________.
解析:根据第一象限内点的坐标的符号特征,横坐标为正,纵坐标为正,可得关于m的不等式m-2>0,
解得m>2.
m>2
记得:第一象限(+,+);第二象限(-,+)
第三象限(-,-);第四象限(+,-).
例5
点A(m+3,m+1)在x轴上,则A点的坐标为( )
A.(0,-2)
B.(2,0)
C.(4,0)
D.(0,-4)
【解析】点A(m+3,m+1)在x轴上,根据x轴上点的坐标特征知m+1=0,求出m的值代入m+3中即可.
B
记得:
x轴上的点(x,0);y轴上的点(0,y).
练一练
已知点P到x轴的距离为2,到y轴的距离为1.如果过点P作两坐标轴的垂线,垂足分别在x轴的正半轴上和y轴的负半轴上,那么点P的坐标是( )
A.(2,-1)
B.(1,-2)
C.(-2,-1)
D.(1,2)
记得:
可通过作图,逐步探究:先考虑所在象限,再确定具体位置。
B
2.已知P点坐标为(a+1,a-3)
①点P在x轴上,则a=
;
②点P在y轴上,则a=
;
3.若点P(x,y)在第四象限,|x|=5,|y|=4,则P点的坐标为
.
3
(5,-4)
-1
1.已知a那么点P(a,-b)在第
象限.
二
拓展练习
7.1
平面直角坐标系
第七章
平面直角坐标系
7.1.2
平面直角坐标系
1.理解并能画出平面直角坐标系;
2.
能写出坐标系内点的坐标;
3.能根据点的坐标把点描到坐标系内;
4.掌握x轴和y轴上点的坐标特征。
学习目标(一)
自学指导
自学课本66页内容,思考:
1、回忆:实数与数轴上的点存在什么关系?
2、要确定平面内的一个点,需要怎样表示呢?
3、什么是平面直角坐标系?它由哪些元素构成?
4、用平面直角坐标系表示点时,数对按怎样顺序表示?
5、原点O的坐标是什么?X轴和y轴上的点的坐标有什么特征?
思考1
如图,数轴上的点A、B表示的数是什么?
表示数字4的点是哪个点?
思考2
由思考1你发现数轴上的点与实数是什么关系?
一一对应
数轴上的每个点都对应一个实数(这个实数叫作这个点在数轴上的坐标);
A点表示
-3;
B点表示2.
表示数字4的是点C
讲授新课
一、
思考:小丽能根据小明的提示从左图中找出图书馆的位置吗?
周末小明和小丽约好一起去图书馆学习.小明告诉小丽,图书馆在中山北路西边50米,人民西路北边30米的位置.
找一找
若将中山路与人民路看成两条互相垂直的数轴,十字路口为它们的公共原点,这样就形成了一个平面直角坐标系.
x
y
o
30
20
10
20
10
-10
-20
-30
-40
-20
-50
-10
-70
-60
-50
-40
-30
-80
(-50,
北
西
30)
人民路
中山路
O
y
在平面内画两条互相垂直、原点重合的数轴,构成平面直角坐标系.
1
2
3
4
5
-4
-3
-2
-1
x
竖直的叫y轴或纵轴;
y轴取向上为正方向
水平的叫x轴或横轴;
x轴取向右为正方向
x轴与y轴的交点叫平面直角坐标系的原点.
知识点一
x
O
下面四个图形中,是平面直角坐标系的是(
)
x
x
y
(A)
3
2
1
-1
-2
-3
x
y
(B)
2
1
-1
-2
O
D
练一练1
这样P点的横坐标是-2,纵坐标是3,规定把横坐标写在前,纵坐标在后,记作:P
(-2,3)
P
(-2,3)就叫做点P在平面直角坐标系中的坐标,简称点P的坐标.
思考:如图,点P如何表示呢?
后由P点向y轴画垂线,垂足N在y轴上的坐标是3.
称为P点的纵坐标.
先由P点向x轴画垂线,垂足M
在x轴上的坐标是-2;称为P点的横坐标.
P
N
M
知识点二
1
1
-1
-2
-3
-4
2
3
2
3
4
5
4
-1
-2
-3
-4
-5
o
A
(4,3)
x
y
1.
写出点A的坐标.
(1)过点A作x轴的垂线,垂足在x轴上对应的数是4;
(2)过点A作y轴的垂线,垂足在y轴上对应的数是3;
点A的坐标为(4,3)
试一试
2.
在平面直角坐标系中
确定点
B
(3,-2)位置
由坐标找点的方法:
(1)先在坐标轴上找到表示横坐标与纵坐标的点;
(2)然后过这两点分别作x轴与y轴的垂线;
(3)垂线的交点就是该坐标对应的点.
B
A
B
C
E
F
D
例1:写出下图中的多边形ABCDEF各个顶点的坐标.
1
2
3
4
-1
-2
1
2
3
-1
-2
-3
【答案】
A(-2,0)
B(0,-3)
C(3,-3)
D(4,0)
E(3,3)
F(0,3)
y
O
x
想一想:
x轴和y轴上的点的坐标有什么特征呢?
在直角坐标系中描下列各点:
A(4,3),
B(-2,3),
C(-4,-1),
D(2,-2),
E(0,4)
x
y
练一练2
·
E
学习目标(二)
1.理解“象限”的概念并掌握各象限的位置;
2.掌握各象限内点的坐标符号特征;
3.能根据横、纵坐标的符号确定点的位置.
4.能根据实际情况建立不同的坐标系解决问题。
阅读课本67页—68页内容,思考:
1、什么是“象限”?象限是怎样划分的?
2、想一想,每个象限内点的坐标在符号上有什么特征?
3、数轴上的点与实数一一对应,那么平面内的点和谁有对应关系呢?
4、合作交流,完成68页“探究”
自学指导
在平面直角坐标系中,两条坐标轴(即横轴和纵轴)把平面分成如图所示的Ⅰ,Ⅱ
,Ⅲ,Ⅳ四个区域.
分别称为第一,二,三,四象限.
注意:坐标轴上的点不属于任何一个象限.
活动1:
观察坐标系,填写各象限内的点的坐标的特征:
+
+
+
-
-
-
+
-
交流:不看平面直角坐标系,你能迅速说出A(4,5)
,
B(-2,3),
C(-4,-1),
D(2.5,-2),
E(0,-4)所在的象限吗?
知识点三
点的位置
横坐标的符号
纵坐标的
符号
第一象限
第二象限
第三象限
第四象限
0
+
+
-
-
0
0
0
交流:不看平面直角坐标系,你能迅速说A(4,0),
B(0,3),C(-4,0),E(0,-4),O(0,0)所在的位置吗?
想一想:
观察坐标系,填写坐标轴上的点的坐标的特征:
点的位置
横坐标的符号
纵坐标的符号
在x轴的正半轴上
在x轴的负半轴上
在y轴的正半轴上
在y轴的负半轴上
例2:在平面直角坐标系中,描出下列各点,并说出它们分别在哪个象限.
A(5,4),B(-3,4),C
(-4
,-1),
D(2,-4).
问题.
坐标平面内的点与有序数对(坐标)是什么关系?
类似“数轴上的点与实数一一对应”
我们可以得出:
坐标平面内的点与有序数对是一一对应的.
完成课本70页第5题
练一练3
建立坐标系求图形中点的坐标
问题:正方形ABCD的边长为4,请建立一个平面直角坐标系,并写出正方形的四个顶点A,B,C,D在这个平面直角坐标系中的坐标.
A
B
C
D
三、
(O)
x
y
解:如图,正方形四个顶点A,B,C,D的坐标分别为:
A(0,0),
B(4,0),
C(4,4),
D(0,4).
A
B
C
D
A(0,-4),
B(4,-4),C(4,0),
D(0,0).
想一想:还可以建立其他平面直角坐标系,表示正方形的四个顶点A,B,C,D的坐标吗?
A(-4,0),
B(0,0),C(0,4),
D(-4,4).
A(-4,-4),
B(0,-4),C(0,0),
D(-4,0).
A(-2,-2),
B(2,-2),C(2,2),
D(-2,2).
由上得知,建立的平面直角坐标系不同,则各点的坐标也不同.
【总结】
建立平面直角坐标系,一般要使图形上的点的坐标便于确定。
需要说明的是,虽然建立不同的平面直角坐标系,同一个点会有不同的坐标,但正方形的形状和性质不会改变.
知识点四
例3:长方形的两条边长分别为4,6,建立适当的直角坐标系,使它的一个顶点的坐标为(-2,-3).请你写出另外三个顶点的坐标.
解:如图,
建立直角坐标系,
∵长方形的一个顶点的坐标为A(-2,-3),
∴长方形的另外三个顶点的坐标分别为
B(2,-3),
C(2,3),D(-2,3).
右图是一个围棋棋盘(局部),把这个围棋棋盘放置在一个平面直角坐标系中,白棋①的坐标是(-2,-1),白棋③的坐标是(-1,-3),则黑棋?的坐标是_______.
练一练4
(1,-2)
y
x
O
当堂练习
1.如图,点A的坐标为(
)
A.
(
-2,3)
B.
(
2,-3)
C
.
(
-2,-3)
D
.
(
2,3)
x
y
O
1
2
3
-3
-2
-1
1
2
-1
-2
A
A
2.如图,点A的坐标为
,
点B的坐标为
.
x
y
O
1
2
3
-3
-2
-1
1
2
-1
-2
A
B
(-2,0)
(0,-2)
3.在
y轴上的点的横坐标是______,
在
x轴上的点的纵坐标是
______.
4.点
M(-
8,12)到
x轴的距离是_______,
到
y轴的距离是
_________
.
0
0
12
8
A(3,6)
B(0,-8)
C(-7,-5)
D(-6,0)
E(-3.6,5)
F(5,-6)
G(0,0)
第一象限
第三象限
第二象限
第四象限
y
轴负半轴
x
轴负半轴
原点
5.下列各点分别在坐标平面的什么位置上?
平面直角坐标系及点的坐标
定义:原点、坐标轴
课堂小结
点的坐标
定义与符号特征
点的坐标的确定
建立合适的平面直角坐标系
课堂作业:
课本70页,第7题。
例4
设点M(a,b)为平面直角坐标系内的点.
(1)当a>0,b<0时,点M位于第几象限?
(2)当ab>0时,点M位于第几象限?
(3)当a为任意有理数,且b<0时,点M位于第几象限?
解:(1)点M在第四象限;
(2)在第一象限(a>0,b>0)或者在第三象限(a<0,b<0);
(3)在第三象限(a<0,b<0)或者第四象限(a>0,b<0)或者在y轴上(a=0,b<0).
延伸拓展
练一练
已在平面直角坐标系中,点P(3,m-2)在第一象限内,则m的取值范围是________.
解析:根据第一象限内点的坐标的符号特征,横坐标为正,纵坐标为正,可得关于m的不等式m-2>0,
解得m>2.
m>2
记得:第一象限(+,+);第二象限(-,+)
第三象限(-,-);第四象限(+,-).
例5
点A(m+3,m+1)在x轴上,则A点的坐标为( )
A.(0,-2)
B.(2,0)
C.(4,0)
D.(0,-4)
【解析】点A(m+3,m+1)在x轴上,根据x轴上点的坐标特征知m+1=0,求出m的值代入m+3中即可.
B
记得:
x轴上的点(x,0);y轴上的点(0,y).
练一练
已知点P到x轴的距离为2,到y轴的距离为1.如果过点P作两坐标轴的垂线,垂足分别在x轴的正半轴上和y轴的负半轴上,那么点P的坐标是( )
A.(2,-1)
B.(1,-2)
C.(-2,-1)
D.(1,2)
记得:
可通过作图,逐步探究:先考虑所在象限,再确定具体位置。
B
2.已知P点坐标为(a+1,a-3)
①点P在x轴上,则a=
;
②点P在y轴上,则a=
;
3.若点P(x,y)在第四象限,|x|=5,|y|=4,则P点的坐标为
.
3
(5,-4)
-1
1.已知a
象限.
二
拓展练习
