2020年苏科版八年级数学第九单元《平行四边》中考真题提优单元测试(有答案)
文档属性
| 名称 | 2020年苏科版八年级数学第九单元《平行四边》中考真题提优单元测试(有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 364.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-28 15:51:24 | ||
图片预览

文档简介
2020年苏科版八年级数学第九单元《平行四边》中考真题提优单元测试(有答案)
一、选择题(24分)
1.(2019.十堰)矩形具有而平行四边形不一定具有的性质是( )
A.对边相等
B.对角相等
C.对角线相等
D.对角线互相平分
2.(2018.徐州)下列图形中,既是轴对称图形,又是中心对称图形的是( )
A.
B.
C.
D.
3.(2018.宿迁)如图,菱形ABCD的对角线AC、BD相交于点O,点E为边CD的中点,若菱形ABCD的周长为16,∠BAD=60°,则△OCE的面积是(??
)
A.?????????????????????????B.?2????????????
???????C.?????????????????????
???D.?4
4.(2019.池河)如图,在△ABC中,D,E分别是AB,BC的中点,点F在DE延长线上,添加一个条件使四边形ADFC为平行四边形,则这个条件是( )
A.∠B=∠F
B.∠B=∠BCF
C.AC=CF
D.AD=CF
5.(2018.黔南州)如图在?ABCD中,已知AC=4cm,若△ACD的周长为13cm,则?ABCD的周长为( )
A.26cm
B.24cm
C.20cm
D.18cm
6.(2018.宁波)如图,在?ABCD中,对角线AC与BD相交于点O,E是边CD的中点,连结OE.若∠ABC=60°,∠BAC=80°,则∠1的度数为( )
A.50°
B.40°
C.30°
D.20°
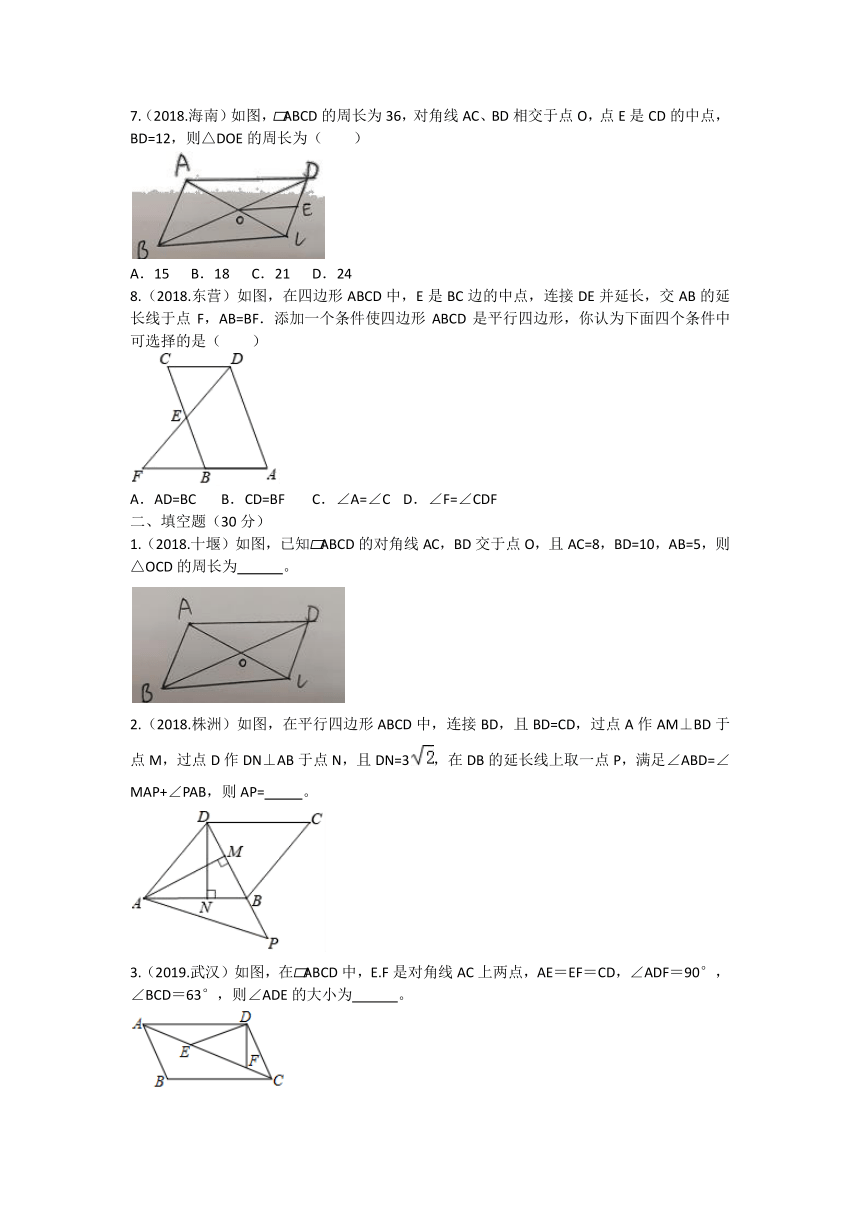
7.(2018.海南)如图,?ABCD的周长为36,对角线AC、BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长为( )
A.15
B.18
C.21
D.24
8.(2018.东营)如图,在四边形ABCD中,E是BC边的中点,连接DE并延长,交AB的延长线于点F,AB=BF.添加一个条件使四边形ABCD是平行四边形,你认为下面四个条件中可选择的是( )
A.AD=BC
B.CD=BF
C.∠A=∠C
D.∠F=∠CDF
二、填空题(30分)
1.(2018.十堰)如图,已知?ABCD的对角线AC,BD交于点O,且AC=8,BD=10,AB=5,则△OCD的周长为
。
2.(2018.株洲)如图,在平行四边形ABCD中,连接BD,且BD=CD,过点A作AM⊥BD于点M,过点D作DN⊥AB于点N,且DN=3,在DB的延长线上取一点P,满足∠ABD=∠MAP+∠PAB,则AP=
。
3.(2019.武汉)如图,在?ABCD中,E.F是对角线AC上两点,AE=EF=CD,∠ADF=90°,∠BCD=63°,则∠ADE的大小为
。
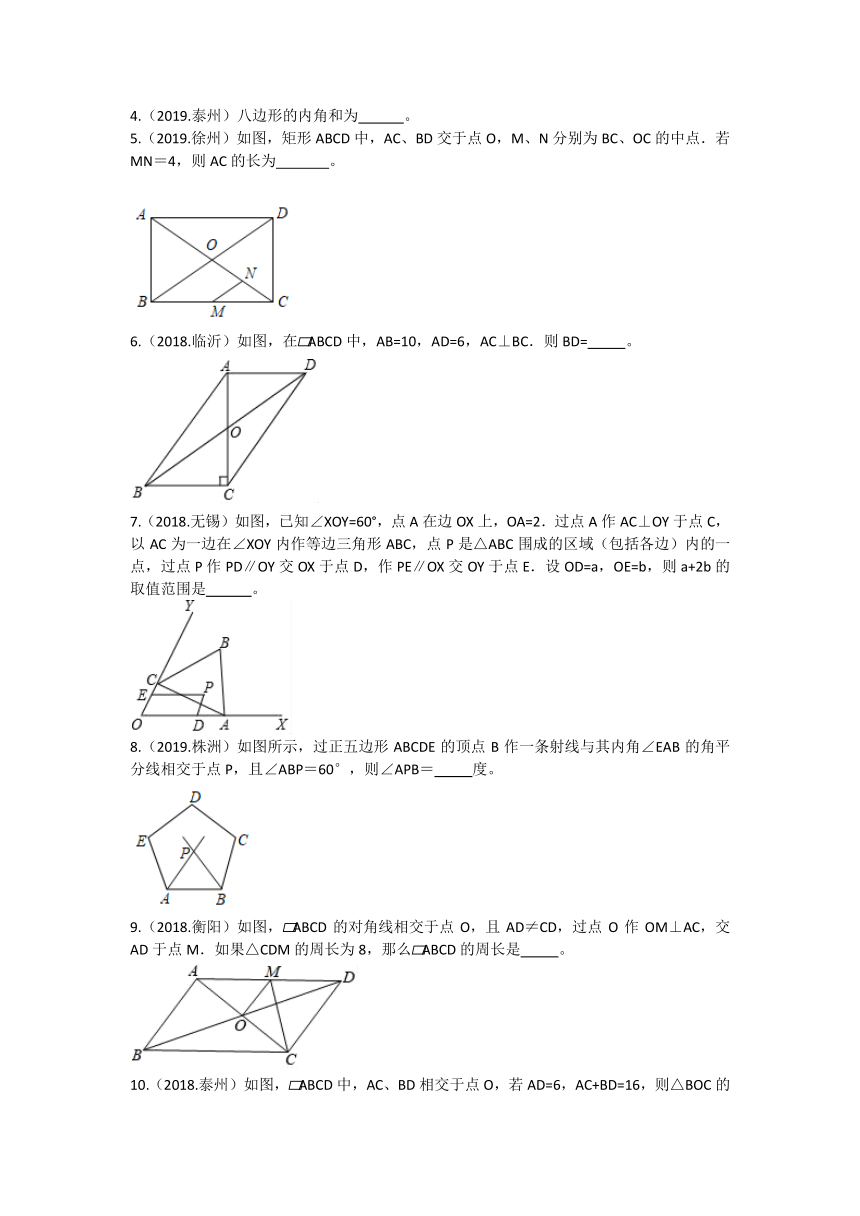
4.(2019.泰州)八边形的内角和为
。
5.(2019.徐州)如图,矩形ABCD中,AC、BD交于点O,M、N分别为BC、OC的中点.若MN=4,则AC的长为
。
6.(2018.临沂)如图,在?ABCD中,AB=10,AD=6,AC⊥BC.则BD=
。
7.(2018.无锡)如图,已知∠XOY=60°,点A在边OX上,OA=2.过点A作AC⊥OY于点C,以AC为一边在∠XOY内作等边三角形ABC,点P是△ABC围成的区域(包括各边)内的一点,过点P作PD∥OY交OX于点D,作PE∥OX交OY于点E.设OD=a,OE=b,则a+2b的取值范围是
。
8.(2019.株洲)如图所示,过正五边形ABCDE的顶点B作一条射线与其内角∠EAB的角平分线相交于点P,且∠ABP=60°,则∠APB=
度。
9.(2018.衡阳)如图,?ABCD的对角线相交于点O,且AD≠CD,过点O作OM⊥AC,交AD于点M.如果△CDM的周长为8,那么?ABCD的周长是
。
10.(2018.泰州)如图,?ABCD中,AC、BD相交于点O,若AD=6,AC+BD=16,则△BOC的周长为
。
三、解答题(66分)
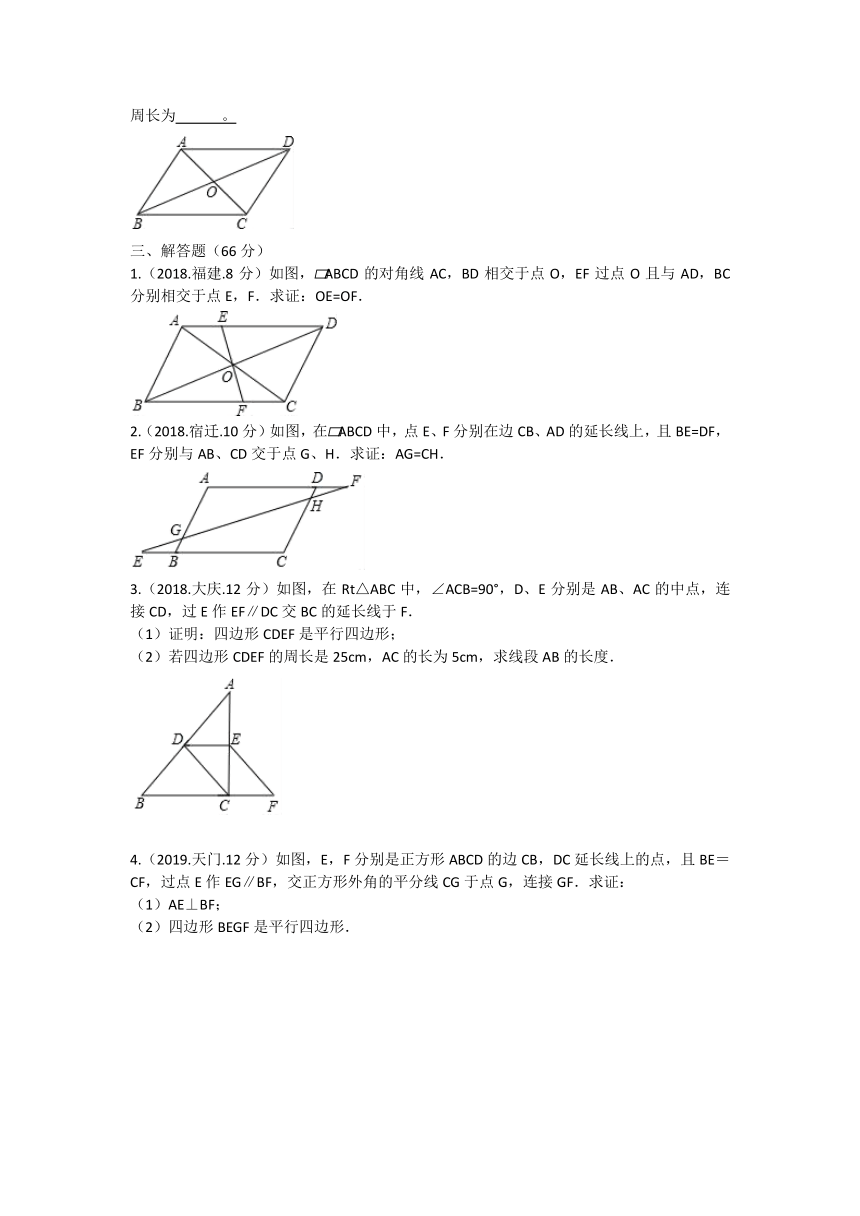
1.(2018.福建.8分)如图,?ABCD的对角线AC,BD相交于点O,EF过点O且与AD,BC分别相交于点E,F.求证:OE=OF.
2.(2018.宿迁.10分)如图,在?ABCD中,点E、F分别在边CB、AD的延长线上,且BE=DF,EF分别与AB、CD交于点G、H.求证:AG=CH.
3.(2018.大庆.12分)如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,连接CD,过E作EF∥DC交BC的延长线于F.
(1)证明:四边形CDEF是平行四边形;
(2)若四边形CDEF的周长是25cm,AC的长为5cm,求线段AB的长度.
4.(2019.天门.12分)如图,E,F分别是正方形ABCD的边CB,DC延长线上的点,且BE=CF,过点E作EG∥BF,交正方形外角的平分线CG于点G,连接GF.求证:
(1)AE⊥BF;
(2)四边形BEGF是平行四边形.
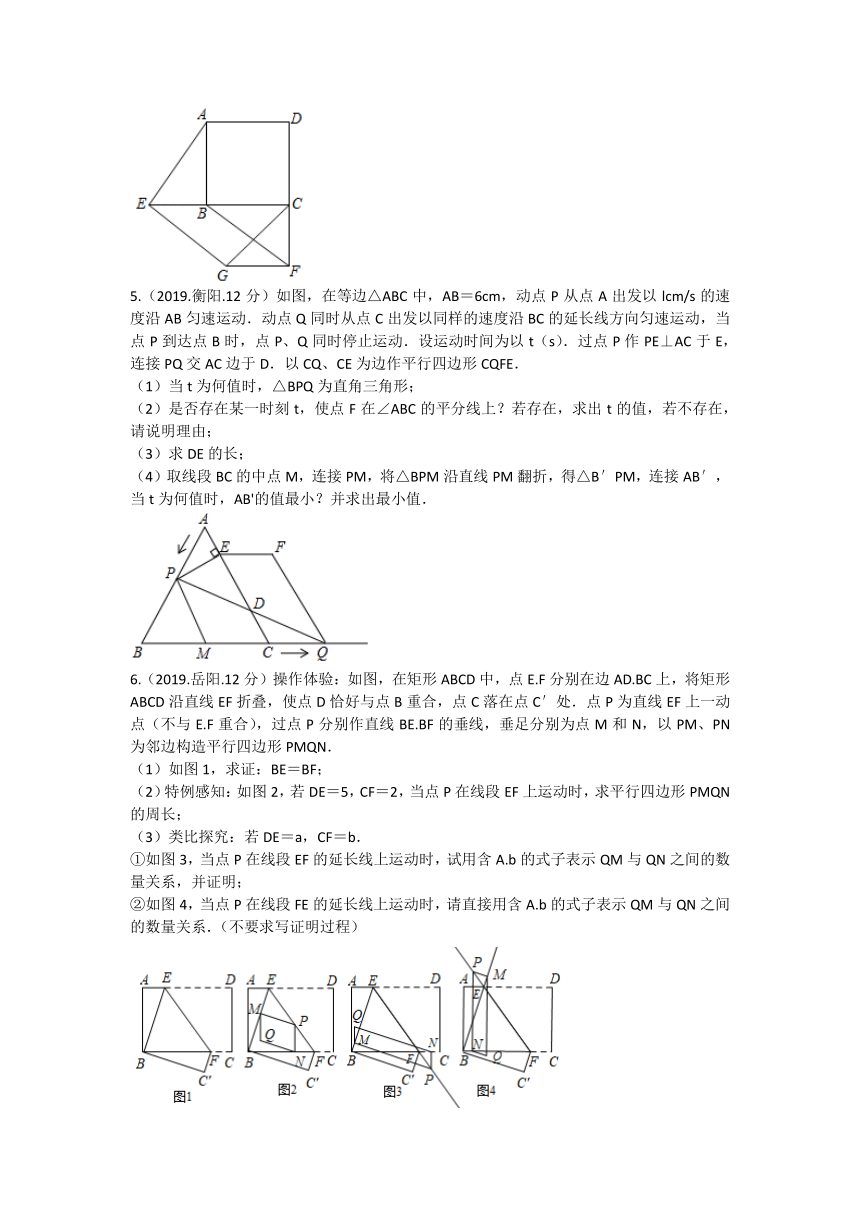
5.(2019.衡阳.12分)如图,在等边△ABC中,AB=6cm,动点P从点A出发以lcm/s的速度沿AB匀速运动.动点Q同时从点C出发以同样的速度沿BC的延长线方向匀速运动,当点P到达点B时,点P、Q同时停止运动.设运动时间为以t(s).过点P作PE⊥AC于E,连接PQ交AC边于D.以CQ、CE为边作平行四边形CQFE.
(1)当t为何值时,△BPQ为直角三角形;
(2)是否存在某一时刻t,使点F在∠ABC的平分线上?若存在,求出t的值,若不存在,请说明理由;
(3)求DE的长;
(4)取线段BC的中点M,连接PM,将△BPM沿直线PM翻折,得△B′PM,连接AB′,当t为何值时,AB'的值最小?并求出最小值.
6.(2019.岳阳.12分)操作体验:如图,在矩形ABCD中,点E.F分别在边AD.BC上,将矩形ABCD沿直线EF折叠,使点D恰好与点B重合,点C落在点C′处.点P为直线EF上一动点(不与E.F重合),过点P分别作直线BE.BF的垂线,垂足分别为点M和N,以PM、PN为邻边构造平行四边形PMQN.
(1)如图1,求证:BE=BF;
(2)特例感知:如图2,若DE=5,CF=2,当点P在线段EF上运动时,求平行四边形PMQN的周长;
(3)类比探究:若DE=a,CF=b.
①如图3,当点P在线段EF的延长线上运动时,试用含A.b的式子表示QM与QN之间的数量关系,并证明;
②如图4,当点P在线段FE的延长线上运动时,请直接用含A.b的式子表示QM与QN之间的数量关系.(不要求写证明过程)
答案
一、选择题
1-8,CAABDBAD
二、填空题
1.
14
2.6
3.21°
4.
1080°
5.16
6.4
7.2≤a+2b≤5
8.66
9.16
10.14
三、解答题
1.
证明:∵四边形ABCD是平行四边形,
∴OA=OC,AD∥BC,
∴∠OAE=∠OCF,
在△OAE和△OCF中,
,
∴△AOE≌△COF(ASA),
∴OE=OF.
2.
证明:∵四边形ABCD是平行四边形,
∴AD=BC,∠A=∠C,AD∥BC,
∴∠E=∠F,
∵BE=DF,
∴AF=EC,
在△AGF和△CHE中
,
∴△AGF≌△CHE(ASA),
∴AG=CH.
3.
(1)证明:∵D、E分别是AB、AC的中点,F是BC延长线上的一点,
∴ED是Rt△ABC的中位线,
∴ED∥FC.BC=2DE,
又
EF∥DC,
∴四边形CDEF是平行四边形;
(2)解:∵四边形CDEF是平行四边形;
∴DC=EF,
∵DC是Rt△ABC斜边AB上的中线,
∴AB=2DC,
∴四边形DCFE的周长=AB+BC,
∵四边形DCFE的周长为25cm,AC的长5cm,
∴BC=25﹣AB,
∵在Rt△ABC中,∠ACB=90°,
∴AB2=BC2+AC2,即AB2=(25﹣AB)2+52,
解得,AB=13cm,
4.
证明:(1)∵四边形ABCD是正方形,
∴AB=BC,∠ABC=∠BCD=90°,
∴∠ABE=∠BCF=90°,
在△ABE和△BCF中,,
∴△ABE≌△BCF(SAS),
∴AE=BF,∠BAE=∠CBF,
∵EG∥BF,
∴∠CBF=∠CEG,
∵∠BAE+∠BEA=90°,
∴∠CEG+∠BEA=90°,
∴AE⊥EG,
∴AE⊥BF;
(2)延长AB至点P,使BP=BE,连接EP,如图所示:
则AP=CE,∠EBP=90°,
∴∠P=45°,
∵CG为正方形ABCD外角的平分线,
∴∠ECG=45°,
∴∠P=∠ECG,
由(1)得∠BAE=∠CEG,
在△APE和△ECG中,,
∴△APE≌△ECG(ASA),
∴AE=EG,
∵AE=BF,
∴EG=BF,
∵EG∥BF,
∴四边形BEGF是平行四边形.
5.解:(1)∵△ABC是等边三角形,
∴∠B=60°,
∴当BQ=2BP时,∠BPQ=90°,
∴6+t=2(6﹣t),
∴t=3,
∴t=3时,△BPQ是直角三角形.
(2)存在.
理由:如图1中,连接BF交AC于M.
∵BF平分∠ABC,BA=BC,
∴BF⊥AC,AM=CM=3cm,
∵EF∥BQ,
∴∠EFM=∠FBC=∠ABC=30°,
∴EF=2EM,
∴t=2?(3﹣t),
解得t=3.
(3)如图2中,作PK∥BC交AC于K.
∵△ABC是等边三角形,
∴∠B=∠A=60°,
∵PK∥BC,
∴∠APK=∠B=60°,
∴∠A=∠APK=∠AKP=60°,
∴△APK是等边三角形,
∴PA=PK,
∵PE⊥AK,
∴AE=EK,
∵AP=CQ=PK,∠PKD=∠DCQ,∠PDK=∠QDC,
∴△PKD≌△QCD(AAS),
∴DK=DC,
∴DE=EK+DK=(AK+CK)=AC=3(cm).
(4)如图3中,连接AM,AB′
∵BM=CM=3,AB=AC,
∴AM⊥BC,
∴AM==3,
∵AB′≥AM﹣MB′,
∴AB′≥3﹣3,
∴AB′的最小值为3﹣3.
6.
(1)证明:如图1中,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DEF=∠EFB,
由翻折可知:∠DEF=∠BEF,
∴∠BEF=∠EFB,
∴BE=BF.
(2)解:如图2中,连接BP,作EH⊥BC于H,则四边形ABHE是矩形,EH=AB.
∵DE=EB=BF=5,CF=2,
∴AD=BC=7,AE=2,
在Rt△ABE中,∵∠A=90°,BE=5,AE=2,
∴AB==,
∵S△BEF=S△PBE+S△PBF,PM⊥BE,PN⊥BF,
∴?BF?EH=?BE?PM+?BF?PN,
∵BE=BF,
∴PM+PN=EH=,
∵四边形PMQN是平行四边形,
∴四边形PMQN的周长=2(PM+PN)=2.
(3)①证明:如图3中,连接BP,作EH⊥BC于H.
∵ED=EB=BF=a,CF=b,
∴AD=BC=a+b,
∴AE=AD﹣DE=b,
∴EH=AB=,
∵S△EBP﹣S△BFP=S△EBF,
∴BE?PM﹣?BF?PN=?BF?EH
一、选择题(24分)
1.(2019.十堰)矩形具有而平行四边形不一定具有的性质是( )
A.对边相等
B.对角相等
C.对角线相等
D.对角线互相平分
2.(2018.徐州)下列图形中,既是轴对称图形,又是中心对称图形的是( )
A.
B.
C.
D.
3.(2018.宿迁)如图,菱形ABCD的对角线AC、BD相交于点O,点E为边CD的中点,若菱形ABCD的周长为16,∠BAD=60°,则△OCE的面积是(??
)
A.?????????????????????????B.?2????????????
???????C.?????????????????????
???D.?4
4.(2019.池河)如图,在△ABC中,D,E分别是AB,BC的中点,点F在DE延长线上,添加一个条件使四边形ADFC为平行四边形,则这个条件是( )
A.∠B=∠F
B.∠B=∠BCF
C.AC=CF
D.AD=CF
5.(2018.黔南州)如图在?ABCD中,已知AC=4cm,若△ACD的周长为13cm,则?ABCD的周长为( )
A.26cm
B.24cm
C.20cm
D.18cm
6.(2018.宁波)如图,在?ABCD中,对角线AC与BD相交于点O,E是边CD的中点,连结OE.若∠ABC=60°,∠BAC=80°,则∠1的度数为( )
A.50°
B.40°
C.30°
D.20°
7.(2018.海南)如图,?ABCD的周长为36,对角线AC、BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长为( )
A.15
B.18
C.21
D.24
8.(2018.东营)如图,在四边形ABCD中,E是BC边的中点,连接DE并延长,交AB的延长线于点F,AB=BF.添加一个条件使四边形ABCD是平行四边形,你认为下面四个条件中可选择的是( )
A.AD=BC
B.CD=BF
C.∠A=∠C
D.∠F=∠CDF
二、填空题(30分)
1.(2018.十堰)如图,已知?ABCD的对角线AC,BD交于点O,且AC=8,BD=10,AB=5,则△OCD的周长为
。
2.(2018.株洲)如图,在平行四边形ABCD中,连接BD,且BD=CD,过点A作AM⊥BD于点M,过点D作DN⊥AB于点N,且DN=3,在DB的延长线上取一点P,满足∠ABD=∠MAP+∠PAB,则AP=
。
3.(2019.武汉)如图,在?ABCD中,E.F是对角线AC上两点,AE=EF=CD,∠ADF=90°,∠BCD=63°,则∠ADE的大小为
。
4.(2019.泰州)八边形的内角和为
。
5.(2019.徐州)如图,矩形ABCD中,AC、BD交于点O,M、N分别为BC、OC的中点.若MN=4,则AC的长为
。
6.(2018.临沂)如图,在?ABCD中,AB=10,AD=6,AC⊥BC.则BD=
。
7.(2018.无锡)如图,已知∠XOY=60°,点A在边OX上,OA=2.过点A作AC⊥OY于点C,以AC为一边在∠XOY内作等边三角形ABC,点P是△ABC围成的区域(包括各边)内的一点,过点P作PD∥OY交OX于点D,作PE∥OX交OY于点E.设OD=a,OE=b,则a+2b的取值范围是
。
8.(2019.株洲)如图所示,过正五边形ABCDE的顶点B作一条射线与其内角∠EAB的角平分线相交于点P,且∠ABP=60°,则∠APB=
度。
9.(2018.衡阳)如图,?ABCD的对角线相交于点O,且AD≠CD,过点O作OM⊥AC,交AD于点M.如果△CDM的周长为8,那么?ABCD的周长是
。
10.(2018.泰州)如图,?ABCD中,AC、BD相交于点O,若AD=6,AC+BD=16,则△BOC的周长为
。
三、解答题(66分)
1.(2018.福建.8分)如图,?ABCD的对角线AC,BD相交于点O,EF过点O且与AD,BC分别相交于点E,F.求证:OE=OF.
2.(2018.宿迁.10分)如图,在?ABCD中,点E、F分别在边CB、AD的延长线上,且BE=DF,EF分别与AB、CD交于点G、H.求证:AG=CH.
3.(2018.大庆.12分)如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,连接CD,过E作EF∥DC交BC的延长线于F.
(1)证明:四边形CDEF是平行四边形;
(2)若四边形CDEF的周长是25cm,AC的长为5cm,求线段AB的长度.
4.(2019.天门.12分)如图,E,F分别是正方形ABCD的边CB,DC延长线上的点,且BE=CF,过点E作EG∥BF,交正方形外角的平分线CG于点G,连接GF.求证:
(1)AE⊥BF;
(2)四边形BEGF是平行四边形.
5.(2019.衡阳.12分)如图,在等边△ABC中,AB=6cm,动点P从点A出发以lcm/s的速度沿AB匀速运动.动点Q同时从点C出发以同样的速度沿BC的延长线方向匀速运动,当点P到达点B时,点P、Q同时停止运动.设运动时间为以t(s).过点P作PE⊥AC于E,连接PQ交AC边于D.以CQ、CE为边作平行四边形CQFE.
(1)当t为何值时,△BPQ为直角三角形;
(2)是否存在某一时刻t,使点F在∠ABC的平分线上?若存在,求出t的值,若不存在,请说明理由;
(3)求DE的长;
(4)取线段BC的中点M,连接PM,将△BPM沿直线PM翻折,得△B′PM,连接AB′,当t为何值时,AB'的值最小?并求出最小值.
6.(2019.岳阳.12分)操作体验:如图,在矩形ABCD中,点E.F分别在边AD.BC上,将矩形ABCD沿直线EF折叠,使点D恰好与点B重合,点C落在点C′处.点P为直线EF上一动点(不与E.F重合),过点P分别作直线BE.BF的垂线,垂足分别为点M和N,以PM、PN为邻边构造平行四边形PMQN.
(1)如图1,求证:BE=BF;
(2)特例感知:如图2,若DE=5,CF=2,当点P在线段EF上运动时,求平行四边形PMQN的周长;
(3)类比探究:若DE=a,CF=b.
①如图3,当点P在线段EF的延长线上运动时,试用含A.b的式子表示QM与QN之间的数量关系,并证明;
②如图4,当点P在线段FE的延长线上运动时,请直接用含A.b的式子表示QM与QN之间的数量关系.(不要求写证明过程)
答案
一、选择题
1-8,CAABDBAD
二、填空题
1.
14
2.6
3.21°
4.
1080°
5.16
6.4
7.2≤a+2b≤5
8.66
9.16
10.14
三、解答题
1.
证明:∵四边形ABCD是平行四边形,
∴OA=OC,AD∥BC,
∴∠OAE=∠OCF,
在△OAE和△OCF中,
,
∴△AOE≌△COF(ASA),
∴OE=OF.
2.
证明:∵四边形ABCD是平行四边形,
∴AD=BC,∠A=∠C,AD∥BC,
∴∠E=∠F,
∵BE=DF,
∴AF=EC,
在△AGF和△CHE中
,
∴△AGF≌△CHE(ASA),
∴AG=CH.
3.
(1)证明:∵D、E分别是AB、AC的中点,F是BC延长线上的一点,
∴ED是Rt△ABC的中位线,
∴ED∥FC.BC=2DE,
又
EF∥DC,
∴四边形CDEF是平行四边形;
(2)解:∵四边形CDEF是平行四边形;
∴DC=EF,
∵DC是Rt△ABC斜边AB上的中线,
∴AB=2DC,
∴四边形DCFE的周长=AB+BC,
∵四边形DCFE的周长为25cm,AC的长5cm,
∴BC=25﹣AB,
∵在Rt△ABC中,∠ACB=90°,
∴AB2=BC2+AC2,即AB2=(25﹣AB)2+52,
解得,AB=13cm,
4.
证明:(1)∵四边形ABCD是正方形,
∴AB=BC,∠ABC=∠BCD=90°,
∴∠ABE=∠BCF=90°,
在△ABE和△BCF中,,
∴△ABE≌△BCF(SAS),
∴AE=BF,∠BAE=∠CBF,
∵EG∥BF,
∴∠CBF=∠CEG,
∵∠BAE+∠BEA=90°,
∴∠CEG+∠BEA=90°,
∴AE⊥EG,
∴AE⊥BF;
(2)延长AB至点P,使BP=BE,连接EP,如图所示:
则AP=CE,∠EBP=90°,
∴∠P=45°,
∵CG为正方形ABCD外角的平分线,
∴∠ECG=45°,
∴∠P=∠ECG,
由(1)得∠BAE=∠CEG,
在△APE和△ECG中,,
∴△APE≌△ECG(ASA),
∴AE=EG,
∵AE=BF,
∴EG=BF,
∵EG∥BF,
∴四边形BEGF是平行四边形.
5.解:(1)∵△ABC是等边三角形,
∴∠B=60°,
∴当BQ=2BP时,∠BPQ=90°,
∴6+t=2(6﹣t),
∴t=3,
∴t=3时,△BPQ是直角三角形.
(2)存在.
理由:如图1中,连接BF交AC于M.
∵BF平分∠ABC,BA=BC,
∴BF⊥AC,AM=CM=3cm,
∵EF∥BQ,
∴∠EFM=∠FBC=∠ABC=30°,
∴EF=2EM,
∴t=2?(3﹣t),
解得t=3.
(3)如图2中,作PK∥BC交AC于K.
∵△ABC是等边三角形,
∴∠B=∠A=60°,
∵PK∥BC,
∴∠APK=∠B=60°,
∴∠A=∠APK=∠AKP=60°,
∴△APK是等边三角形,
∴PA=PK,
∵PE⊥AK,
∴AE=EK,
∵AP=CQ=PK,∠PKD=∠DCQ,∠PDK=∠QDC,
∴△PKD≌△QCD(AAS),
∴DK=DC,
∴DE=EK+DK=(AK+CK)=AC=3(cm).
(4)如图3中,连接AM,AB′
∵BM=CM=3,AB=AC,
∴AM⊥BC,
∴AM==3,
∵AB′≥AM﹣MB′,
∴AB′≥3﹣3,
∴AB′的最小值为3﹣3.
6.
(1)证明:如图1中,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DEF=∠EFB,
由翻折可知:∠DEF=∠BEF,
∴∠BEF=∠EFB,
∴BE=BF.
(2)解:如图2中,连接BP,作EH⊥BC于H,则四边形ABHE是矩形,EH=AB.
∵DE=EB=BF=5,CF=2,
∴AD=BC=7,AE=2,
在Rt△ABE中,∵∠A=90°,BE=5,AE=2,
∴AB==,
∵S△BEF=S△PBE+S△PBF,PM⊥BE,PN⊥BF,
∴?BF?EH=?BE?PM+?BF?PN,
∵BE=BF,
∴PM+PN=EH=,
∵四边形PMQN是平行四边形,
∴四边形PMQN的周长=2(PM+PN)=2.
(3)①证明:如图3中,连接BP,作EH⊥BC于H.
∵ED=EB=BF=a,CF=b,
∴AD=BC=a+b,
∴AE=AD﹣DE=b,
∴EH=AB=,
∵S△EBP﹣S△BFP=S△EBF,
∴BE?PM﹣?BF?PN=?BF?EH
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
