1.4.2 正弦函数、余弦函数的性质-广东省揭阳市第三中学人教A版高中数学必修四课件 (共16张PPT)
文档属性
| 名称 | 1.4.2 正弦函数、余弦函数的性质-广东省揭阳市第三中学人教A版高中数学必修四课件 (共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 744.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-30 10:04:17 | ||
图片预览




文档简介
(共16张PPT)
1.4.2
正弦函数、余弦函数的性质(三)
1、结合正余弦曲线理解三角函数的单调性、最值;
2、利用单调性比较两个三角函数值的大小;
3、能求正、余弦函数的最值。
教学目标:
教学重点:
正余弦函数的单调性
教学难点:
正余弦函数单调性的理解与应用
课
型:新授课
上课时间:2020.3
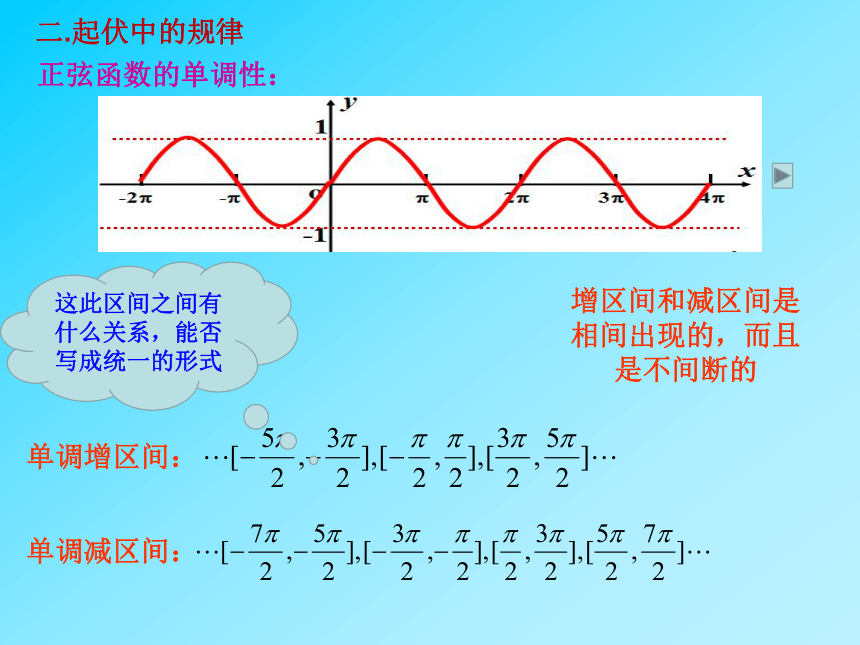
二.起伏中的规律
正弦函数的单调性:
单调增区间:
单调减区间:
这此区间之间有什么关系,能否写成统一的形式
增区间和减区间是相间出现的,而且是不间断的
为什么正弦函数的单调区间,对称轴和对称中心都可以写成统一的形式,归根结底是因为正弦函数具有周期性
也就是说,对于一个周期函数,只要能够研究出一个周期内的单调性,那么整个定义域内的单调性也都明了啦。
那么对于正弦函数来说,我们要研究它在哪个周期内的单调性呢?
为什么不根据“五点法”研究它在
的单调性呢?
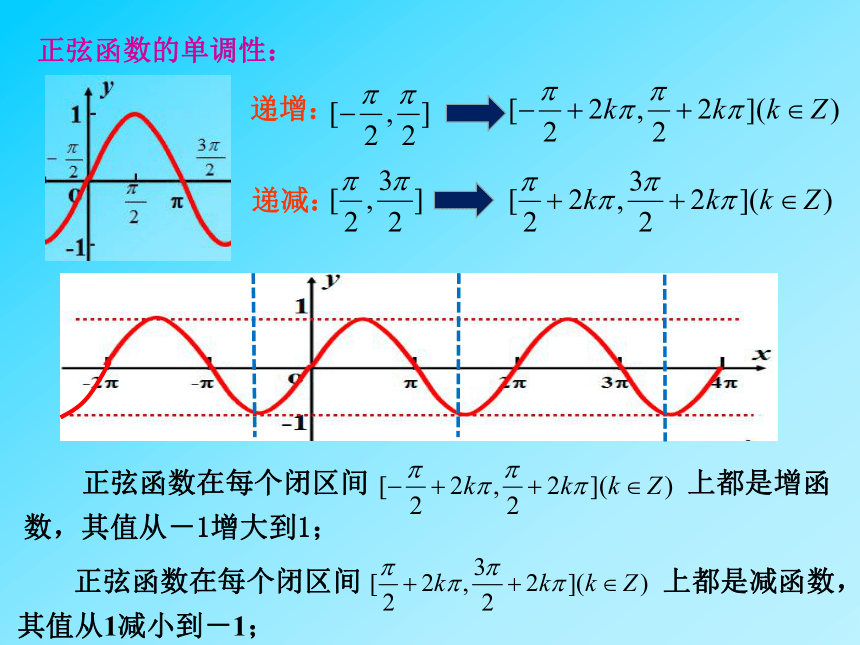
正弦函数的单调性:
递增:
递减:
正弦函数在每个闭区间
上都是增函数,其值从-1增大到1;
正弦函数在每个闭区间
上都是减函数,其值从1减小到-1;
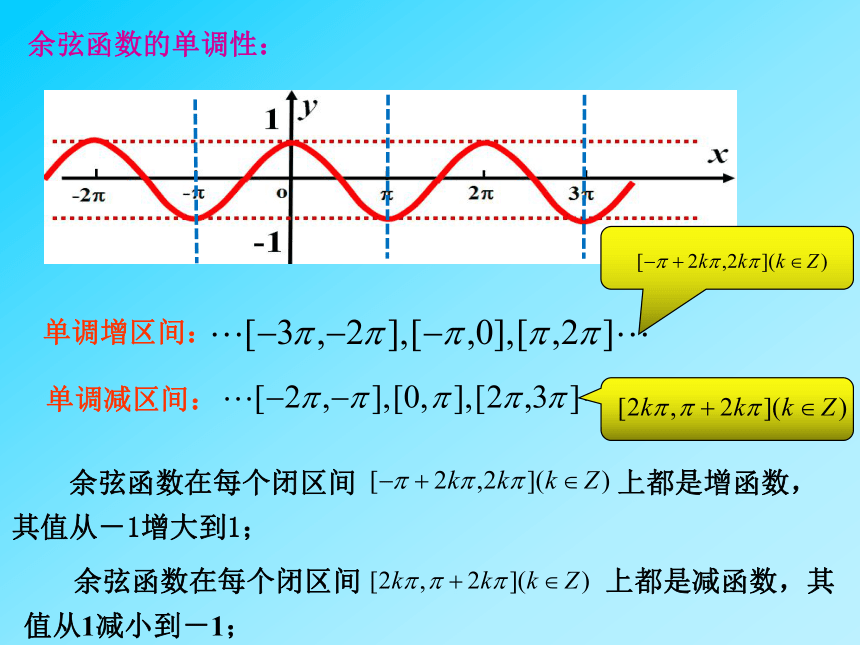
余弦函数的单调性:
单调增区间:
单调减区间:
余弦函数在每个闭区间
上都是增函数,其值从-1增大到1;
余弦函数在每个闭区间
上都是减函数,其值从1减小到-1;
练习:P40
B
例4
利用三角函数的单调性,比较下列各组数的大小。
解:
(1)利用诱导公式将角转化到同
一个单区间内再比较
(2)函数名不同要化相同
练习1
C
正弦函数的最值:
正弦函数当且仅当x=__________
时,取最大值____;
当且仅当x=__________
时取最小值_____;
最值都是在对称轴的地方取得
1
-1
余弦函数的最值:
余弦函数当且仅当x=__________
时,取最大值____;
当且仅当x=__________
时取最小值_____;
最值都是在对称轴的地方取得
1
-1
例3.
下列函数有最大、最小值吗?如果有,请写出取最大、最小
值时的自变量x的集合,并说出最大、最小值分别是什么.
解:
把2x看成一个整体z,则y=-3sinz
练习2
求使下列函数取得最大值、最小值的自变量的集合,并
写出最大值、最小值各是多少?
R
R
2π
2π
奇函数
偶函数
解析式
y=sinx
y=cosx
图象
定义域
值域
最小正周期
奇偶性
单调性
单调增区间
单调减区间
最值
最大值
最小值
对称性
对称轴
对称中心
1.4.2
正弦函数、余弦函数的性质(三)
1、结合正余弦曲线理解三角函数的单调性、最值;
2、利用单调性比较两个三角函数值的大小;
3、能求正、余弦函数的最值。
教学目标:
教学重点:
正余弦函数的单调性
教学难点:
正余弦函数单调性的理解与应用
课
型:新授课
上课时间:2020.3
二.起伏中的规律
正弦函数的单调性:
单调增区间:
单调减区间:
这此区间之间有什么关系,能否写成统一的形式
增区间和减区间是相间出现的,而且是不间断的
为什么正弦函数的单调区间,对称轴和对称中心都可以写成统一的形式,归根结底是因为正弦函数具有周期性
也就是说,对于一个周期函数,只要能够研究出一个周期内的单调性,那么整个定义域内的单调性也都明了啦。
那么对于正弦函数来说,我们要研究它在哪个周期内的单调性呢?
为什么不根据“五点法”研究它在
的单调性呢?
正弦函数的单调性:
递增:
递减:
正弦函数在每个闭区间
上都是增函数,其值从-1增大到1;
正弦函数在每个闭区间
上都是减函数,其值从1减小到-1;
余弦函数的单调性:
单调增区间:
单调减区间:
余弦函数在每个闭区间
上都是增函数,其值从-1增大到1;
余弦函数在每个闭区间
上都是减函数,其值从1减小到-1;
练习:P40
B
例4
利用三角函数的单调性,比较下列各组数的大小。
解:
(1)利用诱导公式将角转化到同
一个单区间内再比较
(2)函数名不同要化相同
练习1
C
正弦函数的最值:
正弦函数当且仅当x=__________
时,取最大值____;
当且仅当x=__________
时取最小值_____;
最值都是在对称轴的地方取得
1
-1
余弦函数的最值:
余弦函数当且仅当x=__________
时,取最大值____;
当且仅当x=__________
时取最小值_____;
最值都是在对称轴的地方取得
1
-1
例3.
下列函数有最大、最小值吗?如果有,请写出取最大、最小
值时的自变量x的集合,并说出最大、最小值分别是什么.
解:
把2x看成一个整体z,则y=-3sinz
练习2
求使下列函数取得最大值、最小值的自变量的集合,并
写出最大值、最小值各是多少?
R
R
2π
2π
奇函数
偶函数
解析式
y=sinx
y=cosx
图象
定义域
值域
最小正周期
奇偶性
单调性
单调增区间
单调减区间
最值
最大值
最小值
对称性
对称轴
对称中心
