11.1.2构成空间几何体的基本元素-人教B版(2019)高中数学必修(第四册)课件(共22张PPT)
文档属性
| 名称 | 11.1.2构成空间几何体的基本元素-人教B版(2019)高中数学必修(第四册)课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-30 10:05:50 | ||
图片预览







文档简介
(共22张PPT)
11.1空间几何体
11.1.2构成空间几何体的基本元素
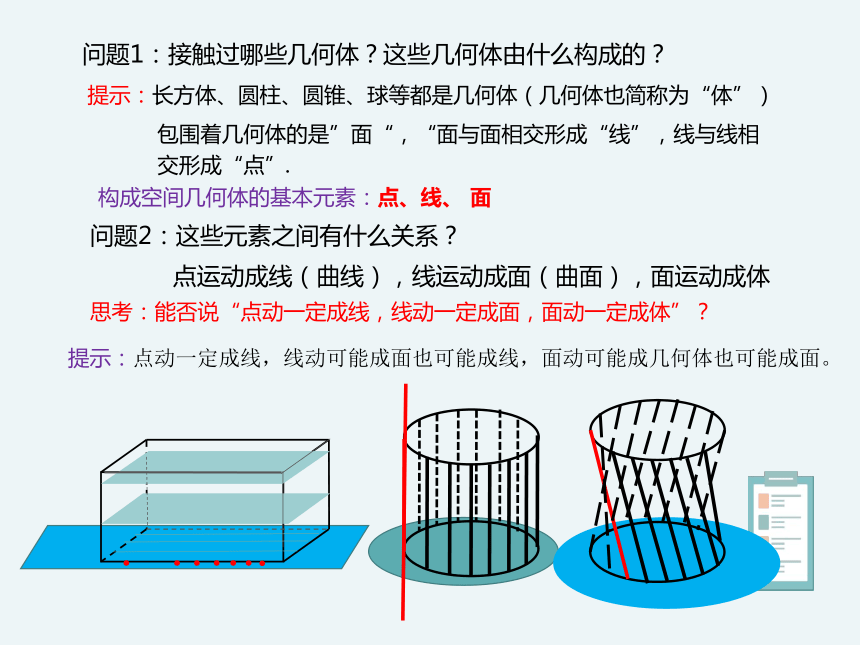
问题1:接触过哪些几何体?这些几何体由什么构成的?
问题2:这些元素之间有什么关系?
提示:长方体、圆柱、圆锥、球等都是几何体(几何体也简称为“体”)
包围着几何体的是”面“,“面与面相交形成“线”,线与线相交形成“点”.
点运动成线(曲线),线运动成面(曲面),面运动成体
思考:能否说“点动一定成线,线动一定成面,面动一定成体”?
构成空间几何体的基本元素:点、线、
面
提示:点动一定成线,线动可能成面也可能成线,面动可能成几何体也可能成面。
立体几何中,我们仍用大写英文字母来表示点.
点,线,面看作构成空间几何体的基本元素.
如图所示的长方体中
AB,BC,CD,DA,AA1,BB1,CC1,DD1,A1B1,B1C1,C1D1,D1A1 ;
A,B,C,D,A1,B1,C1,D1;
ABCD,ABB1A1,BCC1B1,CDD1C1,DAA1D1,A1B1C1D1 ;
6个面可以表示为
而长方体可以表示为ABCD-A1
B1C1D1.
12条棱可以表示为
8个顶点可表示为
构成空间几何体的基本元素是什么?
无大小
处处平直、无厚度、无限延展
无粗细、无限延伸
点:
线:
面:
表示:A、B、C…
表示:a、b、c…或AB、BC…
表示:①平面α,β,γ
,…
讨论:结合长方体或手中的模型讨论,空间中直线与直线(不重合)、直线与平面、平面与平面(不重合)的位置关系
面的画法
②具体几何中常用表示顶点的大写字母表示平面
例:平面ABCD
平面AC或平面BD
α
平面的表示方法
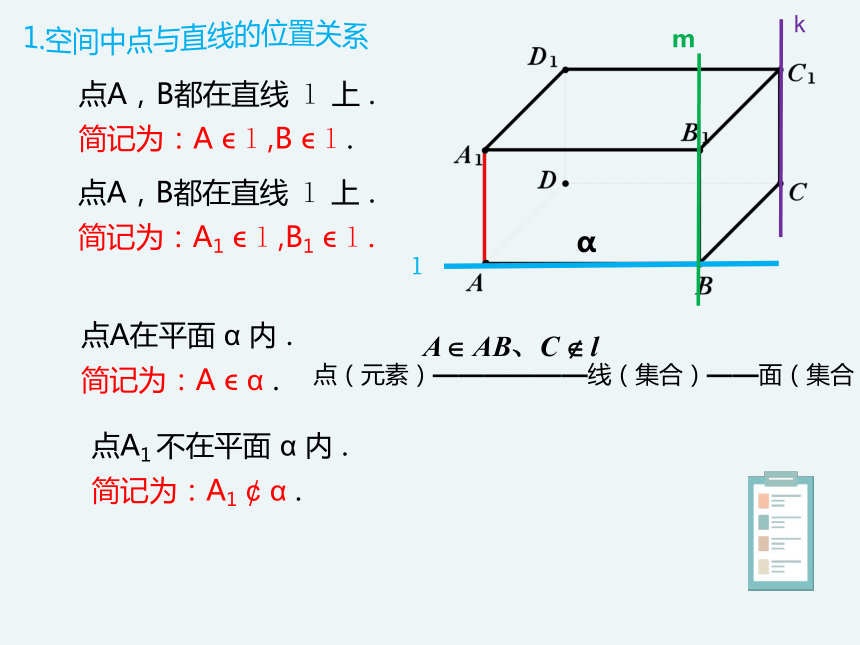
点A,B都在直线
l
上
.
简记为:A
?
l
,B
?
l
.
点A,B都在直线
l
上
.
简记为:A1
?
l
,B1
?
l
.
α
点A在平面
α
内
.
简记为:A
?
α
.
点A1
不在平面
α
内
.
简记为:A1
?
α
.
点(元素)——————线(集合)——面(集合)
直线
l
与
m相交(即有公共点)
.
简记为:l
∩
m=B
或
l
∩
m≠Φ
直线
l
与
k
相交(即没有公共点)
.
简记为:l
∩
k=Φ.
异面直线:空间中的两条直线,可以既不平行,也不相
交,此时称这两条直线异面.
思考:同一平面内的两条直线,如果不相交,就一定平行.这一结论可以推广到空间中的两条直线吗?
不能
α
相交
教材
P66
练B
3、6
线面、面面关系的平面直观图画法:
教材P65
练
A3、4,
练
B1
练习A?利用教室及教室内的物体,举出3对异面直线的例子.
练习A?如果a,b是空间中的两条直线,判断下列命题的真假.
(1)
a与b要么相交,要么不相交;
(2)
a与b要么相交,要么平行;
(3)
当a与b不相交时,a与b要么平行,要么异面.
练习B?用符号表示下列点、线、面的关系.
(1)
点A在直线a上,但不在直线b上
(2)
点P在平面a内,但不在平面β内
(3)
点M在直线
l上,l
平面a内.
补充练习:如图为正方体表面的一种展开图,则图中的四条线段AB,CD,EF,GH在原正方体中互为异面的为________对.
【解析】还原后的正方体如图,
其中AB与CD、AB与GH、EF与GH为异面直线,共3对.
3
3
教材P65页
练习A5、6
线面、面面关系的平面直观图画法:
给定空间中一个平面α及一个点A,过A可以作而且只可以作平面α
的一条垂线.如果记垂足为B,则称B为A在平面α内的射影(也称投影),线段AB为平面α
的垂线段,AB的长为点A到平面α的距离.
特别的,当直线与平面平行时,直线上任意一点到平面的距离称为这条直线到这个平面的距离;
当平面与平面平行时,一个平面上任意一点到另一个平面的距离称为这两平行平面之间的距离.
教材P65页
练习B
2、
P66页
练习B
4
练习B?用符号表示下列点、线、面的关系.
(1)直线a与直线b平行;
(3)平面a与平面b平行
练习B?在长方体ABCD-A1B1C1D1中,写出所有
(1)
与直线AB平行的直线,并用
//
表示;
(2)
与直线AA1异面的直线;
(3)
与直线AB平行的平面,并用合适的符号表示;
(4)
与平面ADD1A1平行的平面,并用合适的符号表示;
(5)与直线AD垂直的平面,并用合适的符号表示.
练习B?已知ABCD-A1B1C1D1
是长方体,且AB=4,
AD
=3,
AA1=2.
(1)写出点A到平面BCC1B1的距离;
(2)
写出直线AB到平面A1B1CQ1的距离;
(3)
写出平面ADD1A1与平面BCC1B1之间的距离.
教材P66页
练习B
5
1.
观察如图所示的正方体ABCD-A′B′C′D′,然后填空.
(1)点A 直线AB;
(2)直线AB 平面ABCD;
(3)直线AB 平面AA′D′D;
(4)平面AD′ 平面BC′;
(5)平面AD′ 平面A′C′;
(6)点B 平面A′B′C′D′.
空间线线,线面,面面位置关系
课堂小结
谢谢观看
11.1空间几何体
11.1.2构成空间几何体的基本元素
问题1:接触过哪些几何体?这些几何体由什么构成的?
问题2:这些元素之间有什么关系?
提示:长方体、圆柱、圆锥、球等都是几何体(几何体也简称为“体”)
包围着几何体的是”面“,“面与面相交形成“线”,线与线相交形成“点”.
点运动成线(曲线),线运动成面(曲面),面运动成体
思考:能否说“点动一定成线,线动一定成面,面动一定成体”?
构成空间几何体的基本元素:点、线、
面
提示:点动一定成线,线动可能成面也可能成线,面动可能成几何体也可能成面。
立体几何中,我们仍用大写英文字母来表示点.
点,线,面看作构成空间几何体的基本元素.
如图所示的长方体中
AB,BC,CD,DA,AA1,BB1,CC1,DD1,A1B1,B1C1,C1D1,D1A1 ;
A,B,C,D,A1,B1,C1,D1;
ABCD,ABB1A1,BCC1B1,CDD1C1,DAA1D1,A1B1C1D1 ;
6个面可以表示为
而长方体可以表示为ABCD-A1
B1C1D1.
12条棱可以表示为
8个顶点可表示为
构成空间几何体的基本元素是什么?
无大小
处处平直、无厚度、无限延展
无粗细、无限延伸
点:
线:
面:
表示:A、B、C…
表示:a、b、c…或AB、BC…
表示:①平面α,β,γ
,…
讨论:结合长方体或手中的模型讨论,空间中直线与直线(不重合)、直线与平面、平面与平面(不重合)的位置关系
面的画法
②具体几何中常用表示顶点的大写字母表示平面
例:平面ABCD
平面AC或平面BD
α
平面的表示方法
点A,B都在直线
l
上
.
简记为:A
?
l
,B
?
l
.
点A,B都在直线
l
上
.
简记为:A1
?
l
,B1
?
l
.
α
点A在平面
α
内
.
简记为:A
?
α
.
点A1
不在平面
α
内
.
简记为:A1
?
α
.
点(元素)——————线(集合)——面(集合)
直线
l
与
m相交(即有公共点)
.
简记为:l
∩
m=B
或
l
∩
m≠Φ
直线
l
与
k
相交(即没有公共点)
.
简记为:l
∩
k=Φ.
异面直线:空间中的两条直线,可以既不平行,也不相
交,此时称这两条直线异面.
思考:同一平面内的两条直线,如果不相交,就一定平行.这一结论可以推广到空间中的两条直线吗?
不能
α
相交
教材
P66
练B
3、6
线面、面面关系的平面直观图画法:
教材P65
练
A3、4,
练
B1
练习A?利用教室及教室内的物体,举出3对异面直线的例子.
练习A?如果a,b是空间中的两条直线,判断下列命题的真假.
(1)
a与b要么相交,要么不相交;
(2)
a与b要么相交,要么平行;
(3)
当a与b不相交时,a与b要么平行,要么异面.
练习B?用符号表示下列点、线、面的关系.
(1)
点A在直线a上,但不在直线b上
(2)
点P在平面a内,但不在平面β内
(3)
点M在直线
l上,l
平面a内.
补充练习:如图为正方体表面的一种展开图,则图中的四条线段AB,CD,EF,GH在原正方体中互为异面的为________对.
【解析】还原后的正方体如图,
其中AB与CD、AB与GH、EF与GH为异面直线,共3对.
3
3
教材P65页
练习A5、6
线面、面面关系的平面直观图画法:
给定空间中一个平面α及一个点A,过A可以作而且只可以作平面α
的一条垂线.如果记垂足为B,则称B为A在平面α内的射影(也称投影),线段AB为平面α
的垂线段,AB的长为点A到平面α的距离.
特别的,当直线与平面平行时,直线上任意一点到平面的距离称为这条直线到这个平面的距离;
当平面与平面平行时,一个平面上任意一点到另一个平面的距离称为这两平行平面之间的距离.
教材P65页
练习B
2、
P66页
练习B
4
练习B?用符号表示下列点、线、面的关系.
(1)直线a与直线b平行;
(3)平面a与平面b平行
练习B?在长方体ABCD-A1B1C1D1中,写出所有
(1)
与直线AB平行的直线,并用
//
表示;
(2)
与直线AA1异面的直线;
(3)
与直线AB平行的平面,并用合适的符号表示;
(4)
与平面ADD1A1平行的平面,并用合适的符号表示;
(5)与直线AD垂直的平面,并用合适的符号表示.
练习B?已知ABCD-A1B1C1D1
是长方体,且AB=4,
AD
=3,
AA1=2.
(1)写出点A到平面BCC1B1的距离;
(2)
写出直线AB到平面A1B1CQ1的距离;
(3)
写出平面ADD1A1与平面BCC1B1之间的距离.
教材P66页
练习B
5
1.
观察如图所示的正方体ABCD-A′B′C′D′,然后填空.
(1)点A 直线AB;
(2)直线AB 平面ABCD;
(3)直线AB 平面AA′D′D;
(4)平面AD′ 平面BC′;
(5)平面AD′ 平面A′C′;
(6)点B 平面A′B′C′D′.
空间线线,线面,面面位置关系
课堂小结
谢谢观看
