六年级下册数学课件-6.4.1 找规律解决实际问题-人教版(共20张PPT)
文档属性
| 名称 | 六年级下册数学课件-6.4.1 找规律解决实际问题-人教版(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-29 06:53:00 | ||
图片预览




文档简介
(共20张PPT)
null
找规律解决实际问题
六
下
数
学
1
2
3
4
温故知新
新知探究
课堂练习
课堂小结
目
录
CONTENTS
温故知新
学而时习之,不亦说乎
03
1
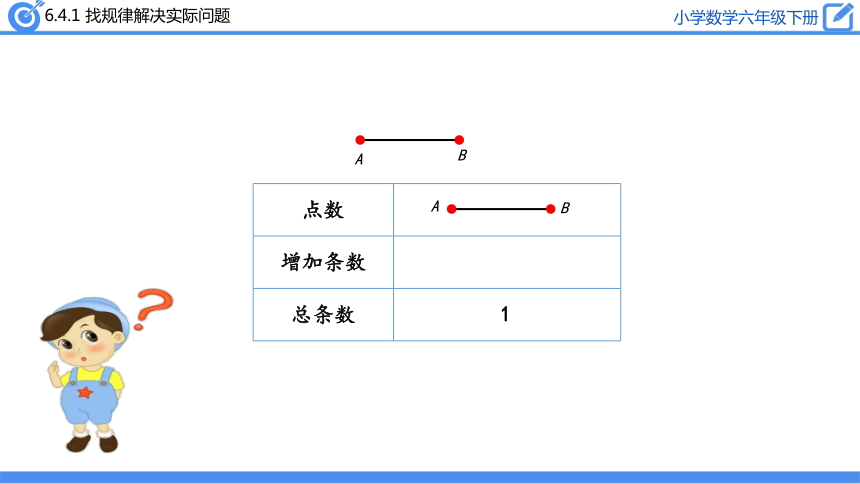
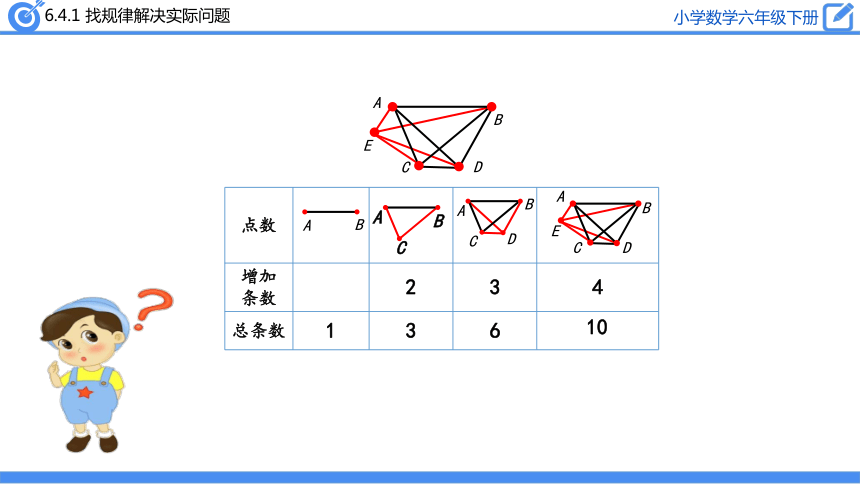
每两个点连成一条线段,一共可以连成多少条线段呢?
找规律。
新知探究
学,然后知不足。
03
2
点数
增加条数
总条数
A
B
A
B
1
点数
增加条数
总条数
1
A
B
C
A
B
A
B
C
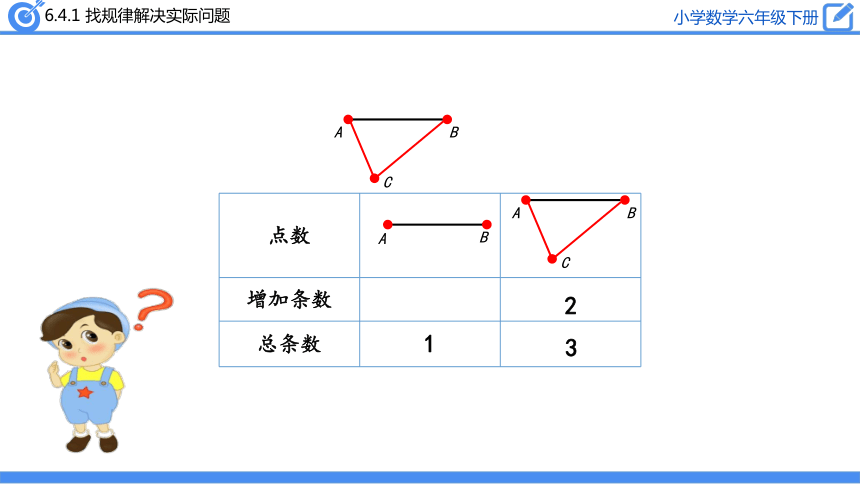
2
3
点数
增加条数
2
总条数
1
3
A
B
C
A
B
C
D
A
B
C
D
A
B
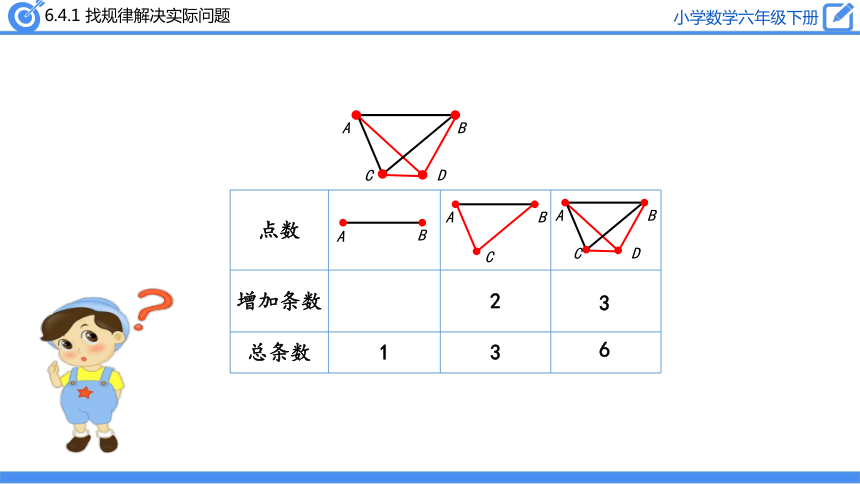
3
6
A
B
C
D
E
点数
增加
条数
2
3
总条数
1
3
6
A
B
C
D
A
B
C
A
B
C
D
E
A
B
4
10
3个点共连:1+2=3(条)
4个点共连:1+2+3=6(条)
点数
2个点
3个点
4个点
5个点
6个点
增加条数
2
3
4
总条数
1
3
6
10
5个点共连:1+2+3+4=10(条)
5
15
6个点共连:1+2+3+4+5=15(条)
有几个点,增加的条数比点数少1。
计算有几条线段,就是从1+2+3+…一直加到比点数少1的数再求和就可以了。
n个点
12个点共连
20个点共连
根据规律,你知道12个点、20个点能连成多少条线段?请写出算式。
1+2+3+4+5+6+7+8+9+10+11=66(条)
1+2+3+…+19=190(条)
1+2+3+…+(n-1)=n(n-1)÷2
这种算式叫做等差数列。
和=(首项+末项)×项数÷2
(1)第7幅图有多少个棋子?第15幅图呢?
1
4
9
16
观察下图,想一想。
(1)
(2)
(3)
(4)
7×7=49(个)
15×15=225(个)
答:第7幅图有49个棋子,第15幅图有225个棋子。
(1)
(2)
(3)
(4)
(2)
每边的棋子数与图形的序号有什么关系?
图形的序号
每边的棋子数
1
2
1
4
3
2
3
4
……
……
答:每边的棋子数与图形的序号相等。
(1)
(2)
(3)
(4)
相等
图形的序号
每边的棋子数
1
2
1
4
3
2
3
4
……
……
(3)第n幅图每边有多少个棋子?一共有多少个棋子?
每行的棋子数×行数=棋子总数
n×n=棋子总数
n2=棋子总数
n
n
答:第n幅图每边有n个棋子,一共有n2个棋子。
课堂练习
纸上得来终觉浅,绝知此事要躬行
03
3
找一找规律,在括号里填上适当的数。
9,11,15,21,29,(
),(
)。
(
2
(
4
(
6
(
8
29+10=39
39
39+12=51
51
1,2,3,1,2,6,1,2,12,(
??
),(
??
),(
??
)。
3×2=6
6×2=12
1
2
12×2=24
24
(1)
(2)
观察下面一组算式,再填出适当的数。
(1)
1×9+2=11
(2)
12×9+3=111
(3)
123×9+4=1111
得数都是由数字1组成的;
第二个加数是几,得数就由几个1组成。
第一个加数是从1开始的自然数按照从小到大的顺序排列的,它的位数
比后面的加数少1。
(4)
1234×9+5=(
)
(5)
12345×9+(
)=111111
(6)
(
)×9+(
)=11111111
11111
6
1234567
8
根据下表中的排列规律,在空格里填上适当的数。
1
4
5
20
2
5
7
35
3
6
9
54
4
3
3
3
1+4=5
2+5=7
3+6=9
4+3=7
4+7=11
7×11=77
4×5=20
5×7=35
6×9=54
上面两个数的差是3
,下面第一个数是上面两个数的和。
下面第二个数是上面第二个数与下面第一个数的乘积。
7
11
77
观察点阵中的规律,画出下一个图形。
1
3
6
10
15
后一个图比前一个图下方多一行圆点,个数比前一个图中最后一行的圆点数多1。
学如蜜蜂采蜜,采过许多花,才能酿出许多蜜。
null
讲师:文小语
null
找规律解决实际问题
六
下
数
学
1
2
3
4
温故知新
新知探究
课堂练习
课堂小结
目
录
CONTENTS
温故知新
学而时习之,不亦说乎
03
1
每两个点连成一条线段,一共可以连成多少条线段呢?
找规律。
新知探究
学,然后知不足。
03
2
点数
增加条数
总条数
A
B
A
B
1
点数
增加条数
总条数
1
A
B
C
A
B
A
B
C
2
3
点数
增加条数
2
总条数
1
3
A
B
C
A
B
C
D
A
B
C
D
A
B
3
6
A
B
C
D
E
点数
增加
条数
2
3
总条数
1
3
6
A
B
C
D
A
B
C
A
B
C
D
E
A
B
4
10
3个点共连:1+2=3(条)
4个点共连:1+2+3=6(条)
点数
2个点
3个点
4个点
5个点
6个点
增加条数
2
3
4
总条数
1
3
6
10
5个点共连:1+2+3+4=10(条)
5
15
6个点共连:1+2+3+4+5=15(条)
有几个点,增加的条数比点数少1。
计算有几条线段,就是从1+2+3+…一直加到比点数少1的数再求和就可以了。
n个点
12个点共连
20个点共连
根据规律,你知道12个点、20个点能连成多少条线段?请写出算式。
1+2+3+4+5+6+7+8+9+10+11=66(条)
1+2+3+…+19=190(条)
1+2+3+…+(n-1)=n(n-1)÷2
这种算式叫做等差数列。
和=(首项+末项)×项数÷2
(1)第7幅图有多少个棋子?第15幅图呢?
1
4
9
16
观察下图,想一想。
(1)
(2)
(3)
(4)
7×7=49(个)
15×15=225(个)
答:第7幅图有49个棋子,第15幅图有225个棋子。
(1)
(2)
(3)
(4)
(2)
每边的棋子数与图形的序号有什么关系?
图形的序号
每边的棋子数
1
2
1
4
3
2
3
4
……
……
答:每边的棋子数与图形的序号相等。
(1)
(2)
(3)
(4)
相等
图形的序号
每边的棋子数
1
2
1
4
3
2
3
4
……
……
(3)第n幅图每边有多少个棋子?一共有多少个棋子?
每行的棋子数×行数=棋子总数
n×n=棋子总数
n2=棋子总数
n
n
答:第n幅图每边有n个棋子,一共有n2个棋子。
课堂练习
纸上得来终觉浅,绝知此事要躬行
03
3
找一找规律,在括号里填上适当的数。
9,11,15,21,29,(
),(
)。
(
2
(
4
(
6
(
8
29+10=39
39
39+12=51
51
1,2,3,1,2,6,1,2,12,(
??
),(
??
),(
??
)。
3×2=6
6×2=12
1
2
12×2=24
24
(1)
(2)
观察下面一组算式,再填出适当的数。
(1)
1×9+2=11
(2)
12×9+3=111
(3)
123×9+4=1111
得数都是由数字1组成的;
第二个加数是几,得数就由几个1组成。
第一个加数是从1开始的自然数按照从小到大的顺序排列的,它的位数
比后面的加数少1。
(4)
1234×9+5=(
)
(5)
12345×9+(
)=111111
(6)
(
)×9+(
)=11111111
11111
6
1234567
8
根据下表中的排列规律,在空格里填上适当的数。
1
4
5
20
2
5
7
35
3
6
9
54
4
3
3
3
1+4=5
2+5=7
3+6=9
4+3=7
4+7=11
7×11=77
4×5=20
5×7=35
6×9=54
上面两个数的差是3
,下面第一个数是上面两个数的和。
下面第二个数是上面第二个数与下面第一个数的乘积。
7
11
77
观察点阵中的规律,画出下一个图形。
1
3
6
10
15
后一个图比前一个图下方多一行圆点,个数比前一个图中最后一行的圆点数多1。
学如蜜蜂采蜜,采过许多花,才能酿出许多蜜。
null
讲师:文小语
