六年级下册数学课件-6.2.3 练习十八-人教版(共21张PPT)
文档属性
| 名称 | 六年级下册数学课件-6.2.3 练习十八-人教版(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-29 06:54:03 | ||
图片预览



文档简介
(共21张PPT)
null
6.2.3
练习十八
六
下
数
学
1
2
3
4
温故知新
新知探究
课堂练习
课堂小结
目
录
CONTENTS
温故知新
学而时习之,不亦说乎
03
1
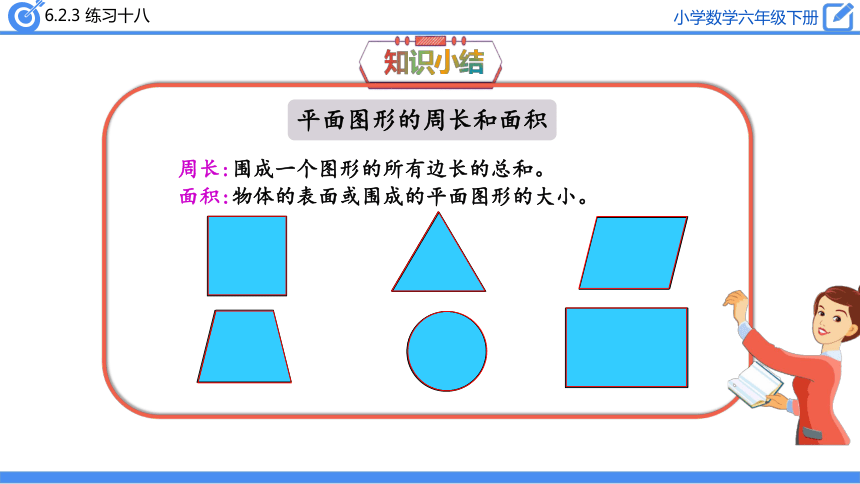
平面图形的周长和面积
面积:物体的表面或围成的平面图形的大小。
周长:围成一个图形的所有边长的总和。
知识小结
a
b
a
.
r
d
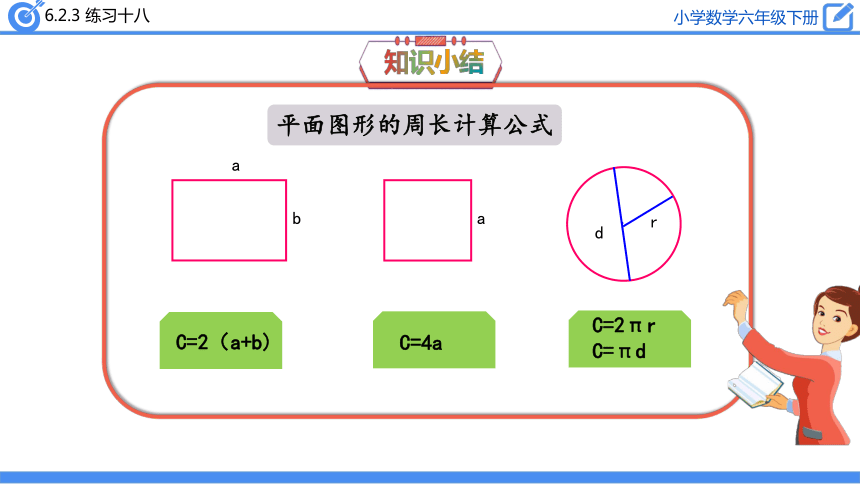
C=2(a+b)
C=4a
C=2πr
C=πd
平面图形的周长计算公式
知识小结
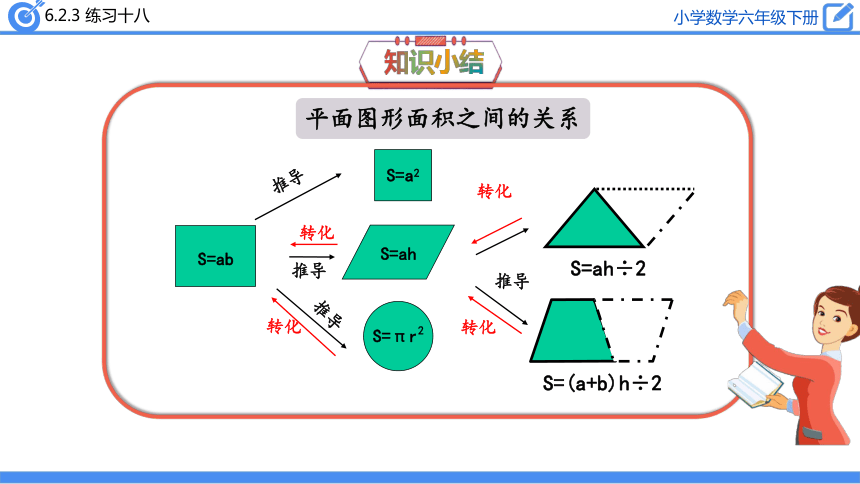
平面图形面积之间的关系
S=πr2
S=ab
S=ah
推导
转化
转化
推导
S=(a+b)h÷2
S=ah÷2
转化
S=a2
转化
推导
推导
知识小结
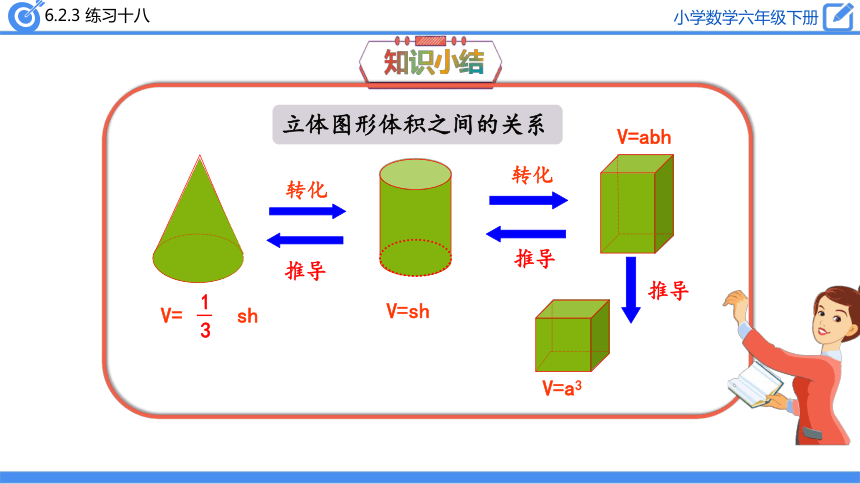
立体图形体积之间的关系
推导
转化
转化
推导
V=abh
V=a3
V=sh
V=
sh
1
3
推导
知识小结
课堂练习
纸上得来终觉浅,绝知此事要躬行
03
3
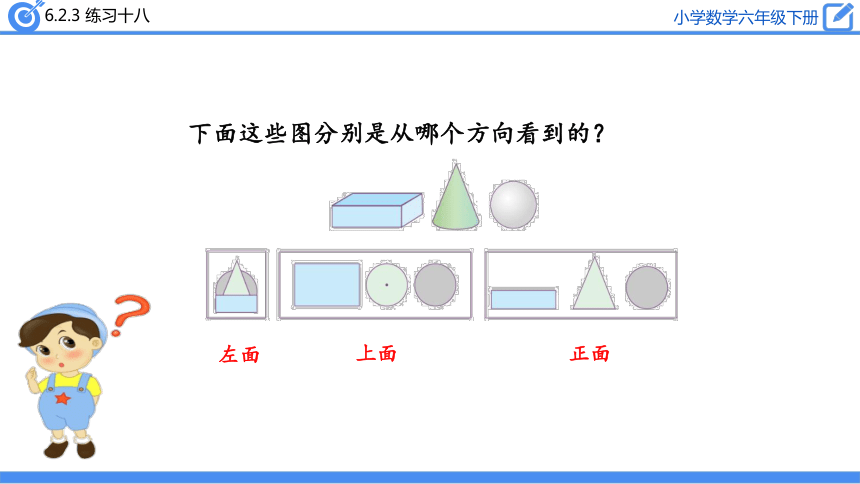
下面这些图分别是从哪个方向看到的?
左面
上面
正面
每一组中两个图形的周长相等吗?面积呢?
长方形和平行四边形面积相等,周长不等。
周长相等,面积不等。
两个平面图形的面积相等,周长不一定相等。
两个平面图形的周长相等,面积不一定相等。
6×3÷2×2
答:正方形的面积是18平方分米。
把一个直径是6分米的圆剪成一个最大的正方形,这个正方形的面积是多少?
d=6dm
=18÷2×2
=18(平方分米)
时针长12厘米,如果走一圈,它的尖端走过的路程是多少?分针长18厘米,如果走1小时,它的尖端走过的路程是多少?
2×3.14×12
=6.28×12
=75.36(厘米)
2×3.14×18
=6.28×18
=113.04(厘米)
答:时针走一圈,它的尖端走过的路程是75.36厘米。
答:分针走1小时,它的尖端走过的路程是113.04厘米。
在长12.4厘米,宽7.2厘米的长方形纸中,剪半径是一厘米的圆,能剪多少个?画一画剪一剪。
方法一
方法二
可以剪18个
可以剪22个
把一块棱长10cm的正方体铁块熔铸成一个底面直径是20cm的圆锥形铁块。这个圆锥形铁块的高约是多少?(得数保留整厘米)
V
=103=1000(cm3)
正方体
1
3
V
=
πr2h
圆锥
h=1000×3÷π÷(20÷2)2
≈10(cm)
答:这个圆锥形铁块的高约是10cm。
正方体铁块变成圆锥形铁块,形状变了,前后体积没变。
把一个棱长6cm的正方体切成棱长2cm的小正方体,可以得到多少个小正方体?它们的表面积之和比原来大正方形的表面积增加了多少?
V大正方体=63=216(cm3)
V小正方体=23=8(cm3)
216÷8=27(个)
S大正方体=6×62=216(cm2)
S小正方体=6×22=24(cm2)
24×27-216=432(cm2)
12×62=432(cm2)
答:可以得到27个小正方体。它们的表面积之和比原来大正方形的表面积增加432cm2。
沿长、宽、高三个方向各切2次,共切6次,每切一次增加2个大正方形的面积,共增加12个大正方形的面积。
右图,是由棱长5厘米的正方体搭成的,所有表面涂成了绿色。
答:只有2个面涂色的正方体有2个。
只有3个面涂色的正方体有4个。
只有4个面涂色的正方体有2个。
(1)一共有多少个正方体?它的体积是多少?
(2)只有2个面涂色的正方体,有多少个?
(3)只有3个面涂色的正方体,有多少个?
(4)只有4个面涂色的正方体?
5×5×5×10=1250(cm3)
答:一共有10个正方体,它的体积是1250cm3。
一个,正方体的内部有一个四分之一圆(涂色部分)已知正方形的面积是10cm2的,涂色部分的面积是多少?
3.14×10=31.4(cm2)
正方形的面积是10,圆半径的平方就是10。
31.4×=7.85(cm2)
答:涂色部分的面积是7.85平方厘米。
用长24厘米的铁丝围一个长方体(或正方体)框架。这个长方体的表面糊一层纸,怎样围用纸最多?
用纸最多就是表面积最大
棱长:24÷12=2(cm)
表面积:2×2×6=24(cm2)
围成正方体
棱长之和:24÷4=6(cm)
假设长为3cm,宽为2cm,高为1cm,
表面积:
3×2×2+3×1×2+2×1×2=22(cm2)
围成长方体
答:围成正方体用纸多,最多是24平方厘米。
24>22
课堂小结
学而不思则惘,思而不学则殆
03
4
1.运用平面图形的周长面积的意义及计算
公式,灵活正确进行周长和面积计算。
2.利用体积公式,解决实际问题。
3.体会代数思想,发展创新思维。
知识小结
学如蜜蜂采蜜,采过许多花,才能酿出许多蜜。
null
讲师:文小语
null
6.2.3
练习十八
六
下
数
学
1
2
3
4
温故知新
新知探究
课堂练习
课堂小结
目
录
CONTENTS
温故知新
学而时习之,不亦说乎
03
1
平面图形的周长和面积
面积:物体的表面或围成的平面图形的大小。
周长:围成一个图形的所有边长的总和。
知识小结
a
b
a
.
r
d
C=2(a+b)
C=4a
C=2πr
C=πd
平面图形的周长计算公式
知识小结
平面图形面积之间的关系
S=πr2
S=ab
S=ah
推导
转化
转化
推导
S=(a+b)h÷2
S=ah÷2
转化
S=a2
转化
推导
推导
知识小结
立体图形体积之间的关系
推导
转化
转化
推导
V=abh
V=a3
V=sh
V=
sh
1
3
推导
知识小结
课堂练习
纸上得来终觉浅,绝知此事要躬行
03
3
下面这些图分别是从哪个方向看到的?
左面
上面
正面
每一组中两个图形的周长相等吗?面积呢?
长方形和平行四边形面积相等,周长不等。
周长相等,面积不等。
两个平面图形的面积相等,周长不一定相等。
两个平面图形的周长相等,面积不一定相等。
6×3÷2×2
答:正方形的面积是18平方分米。
把一个直径是6分米的圆剪成一个最大的正方形,这个正方形的面积是多少?
d=6dm
=18÷2×2
=18(平方分米)
时针长12厘米,如果走一圈,它的尖端走过的路程是多少?分针长18厘米,如果走1小时,它的尖端走过的路程是多少?
2×3.14×12
=6.28×12
=75.36(厘米)
2×3.14×18
=6.28×18
=113.04(厘米)
答:时针走一圈,它的尖端走过的路程是75.36厘米。
答:分针走1小时,它的尖端走过的路程是113.04厘米。
在长12.4厘米,宽7.2厘米的长方形纸中,剪半径是一厘米的圆,能剪多少个?画一画剪一剪。
方法一
方法二
可以剪18个
可以剪22个
把一块棱长10cm的正方体铁块熔铸成一个底面直径是20cm的圆锥形铁块。这个圆锥形铁块的高约是多少?(得数保留整厘米)
V
=103=1000(cm3)
正方体
1
3
V
=
πr2h
圆锥
h=1000×3÷π÷(20÷2)2
≈10(cm)
答:这个圆锥形铁块的高约是10cm。
正方体铁块变成圆锥形铁块,形状变了,前后体积没变。
把一个棱长6cm的正方体切成棱长2cm的小正方体,可以得到多少个小正方体?它们的表面积之和比原来大正方形的表面积增加了多少?
V大正方体=63=216(cm3)
V小正方体=23=8(cm3)
216÷8=27(个)
S大正方体=6×62=216(cm2)
S小正方体=6×22=24(cm2)
24×27-216=432(cm2)
12×62=432(cm2)
答:可以得到27个小正方体。它们的表面积之和比原来大正方形的表面积增加432cm2。
沿长、宽、高三个方向各切2次,共切6次,每切一次增加2个大正方形的面积,共增加12个大正方形的面积。
右图,是由棱长5厘米的正方体搭成的,所有表面涂成了绿色。
答:只有2个面涂色的正方体有2个。
只有3个面涂色的正方体有4个。
只有4个面涂色的正方体有2个。
(1)一共有多少个正方体?它的体积是多少?
(2)只有2个面涂色的正方体,有多少个?
(3)只有3个面涂色的正方体,有多少个?
(4)只有4个面涂色的正方体?
5×5×5×10=1250(cm3)
答:一共有10个正方体,它的体积是1250cm3。
一个,正方体的内部有一个四分之一圆(涂色部分)已知正方形的面积是10cm2的,涂色部分的面积是多少?
3.14×10=31.4(cm2)
正方形的面积是10,圆半径的平方就是10。
31.4×=7.85(cm2)
答:涂色部分的面积是7.85平方厘米。
用长24厘米的铁丝围一个长方体(或正方体)框架。这个长方体的表面糊一层纸,怎样围用纸最多?
用纸最多就是表面积最大
棱长:24÷12=2(cm)
表面积:2×2×6=24(cm2)
围成正方体
棱长之和:24÷4=6(cm)
假设长为3cm,宽为2cm,高为1cm,
表面积:
3×2×2+3×1×2+2×1×2=22(cm2)
围成长方体
答:围成正方体用纸多,最多是24平方厘米。
24>22
课堂小结
学而不思则惘,思而不学则殆
03
4
1.运用平面图形的周长面积的意义及计算
公式,灵活正确进行周长和面积计算。
2.利用体积公式,解决实际问题。
3.体会代数思想,发展创新思维。
知识小结
学如蜜蜂采蜜,采过许多花,才能酿出许多蜜。
null
讲师:文小语
