人教A版必修1第三章3.1.1方程的根与函数的零点 一元二次根的分布(共17张PPT)
文档属性
| 名称 | 人教A版必修1第三章3.1.1方程的根与函数的零点 一元二次根的分布(共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 708.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-30 10:31:50 | ||
图片预览





文档简介
(共17张PPT)
函数y=f(x),把使f(x)=0的实数x叫做函数
y=f(x)的零点。
方程f(x)=0有实数根
函数零点的定义:
等价关系
一、复习
如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a)·f(b)<0,那么,函数y=f(x)在区间(a,b)
内有零点,即存在c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0的根。
注:只要满足上述两个条件,就能判断函数在对应区间内存在零点。
零点存在性定理
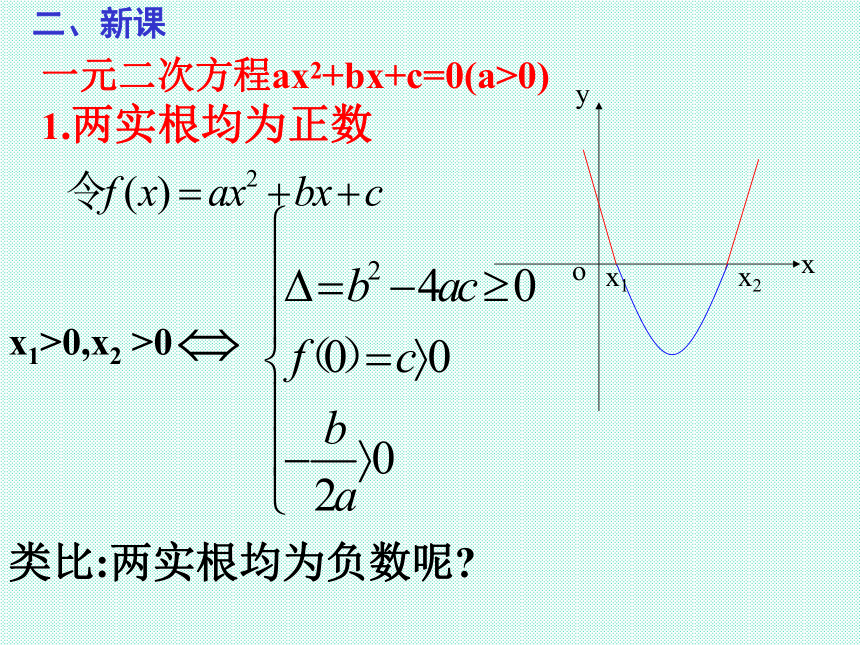
一元二次方程ax2+bx+c=0(a>0)
类比:两实根均为负数呢?
二、新课
1.两实根均为正数
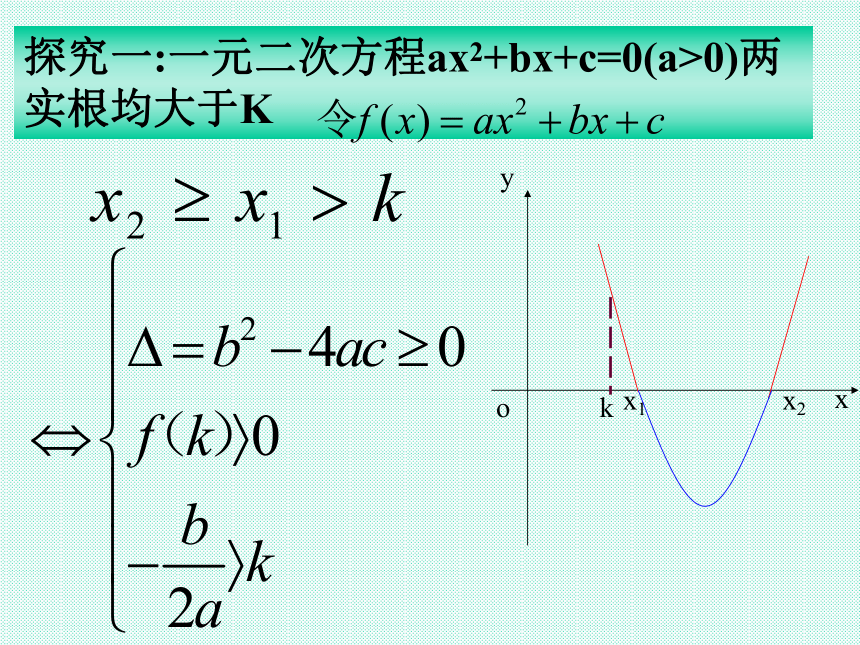
探究一:一元二次方程ax2+bx+c=0(a>0)两实根均大于K
2.一元二次方程ax2+bx+c=0(a>0)
一实根为正数,另一实根为负数
探究二:一元二次方程ax2+bx+c=0(a>0)
一根大于k,另一根小于k
x1例1.关于x的方程x2+(m-3)x+m=0
满足下列条件
,求m的范围
(1)有
两个正的实数根
(2)有两个负的实数根
例1.关于x的方程x2+(m-3)x+m=0
满足下列条件
,求m的范围
(3)有一正一负实根
例1.关于x的方程x2+(m-3)x+m=0
满足下列条件
,求m的范围
(4)两根均大于-1小于2
思考:如何解决此问题呢?
例1.关于x的方程x2+(m-3)x+m=0
满足下列条件
,求m的范围
(5)一根大于-1小于2,另一根
大于3小于5
探究三:一元二次方程ax2+bx+c=0(a>0)两个实数根都在(m,n)
探究四:一元二次方ax2+bx+c=0(a>0)
的一个根在(m,n),另一根在(p,q)
(4)两根均大于-1小于2
(5)一根大于-1小于2,另一根
大于3小于5
例1.关于x的方程x2+(m-3)x+m=0
满足下列条件
,求m的范围
思考:若关于x的方程2kx2-2x-3k-2=0的两根一个小于1,另一根大于1,试求实数k的取值范围。
小结
若关于x的方程ax2+bx+c=0(a>0)实数根的分布问题
1.判别式
2.对称轴
3.特殊点对应的函数值
思想方法——化归思想
数形结合
作业
1、方程5x2-ax-1=0(a∈R)的一个根在区间(-1,0)上,另一个在区间(1,2)上
,求a的取值范围。
2、已知函数f(x)=mx2+(m-3)x+1的图象的零点至少有一个在原点的右侧,求实数m的取值范围。
函数y=f(x),把使f(x)=0的实数x叫做函数
y=f(x)的零点。
方程f(x)=0有实数根
函数零点的定义:
等价关系
一、复习
如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a)·f(b)<0,那么,函数y=f(x)在区间(a,b)
内有零点,即存在c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0的根。
注:只要满足上述两个条件,就能判断函数在对应区间内存在零点。
零点存在性定理
一元二次方程ax2+bx+c=0(a>0)
类比:两实根均为负数呢?
二、新课
1.两实根均为正数
探究一:一元二次方程ax2+bx+c=0(a>0)两实根均大于K
2.一元二次方程ax2+bx+c=0(a>0)
一实根为正数,另一实根为负数
探究二:一元二次方程ax2+bx+c=0(a>0)
一根大于k,另一根小于k
x1
满足下列条件
,求m的范围
(1)有
两个正的实数根
(2)有两个负的实数根
例1.关于x的方程x2+(m-3)x+m=0
满足下列条件
,求m的范围
(3)有一正一负实根
例1.关于x的方程x2+(m-3)x+m=0
满足下列条件
,求m的范围
(4)两根均大于-1小于2
思考:如何解决此问题呢?
例1.关于x的方程x2+(m-3)x+m=0
满足下列条件
,求m的范围
(5)一根大于-1小于2,另一根
大于3小于5
探究三:一元二次方程ax2+bx+c=0(a>0)两个实数根都在(m,n)
探究四:一元二次方ax2+bx+c=0(a>0)
的一个根在(m,n),另一根在(p,q)
(4)两根均大于-1小于2
(5)一根大于-1小于2,另一根
大于3小于5
例1.关于x的方程x2+(m-3)x+m=0
满足下列条件
,求m的范围
思考:若关于x的方程2kx2-2x-3k-2=0的两根一个小于1,另一根大于1,试求实数k的取值范围。
小结
若关于x的方程ax2+bx+c=0(a>0)实数根的分布问题
1.判别式
2.对称轴
3.特殊点对应的函数值
思想方法——化归思想
数形结合
作业
1、方程5x2-ax-1=0(a∈R)的一个根在区间(-1,0)上,另一个在区间(1,2)上
,求a的取值范围。
2、已知函数f(x)=mx2+(m-3)x+1的图象的零点至少有一个在原点的右侧,求实数m的取值范围。
