北师大版七年级数学下册4.1认识三角形(第1课时)课件 (30张PPT)
文档属性
| 名称 | 北师大版七年级数学下册4.1认识三角形(第1课时)课件 (30张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 851.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-29 07:17:14 | ||
图片预览









文档简介
(共30张PPT)
4.1
认识三角形
(第1
课时)
新课引入
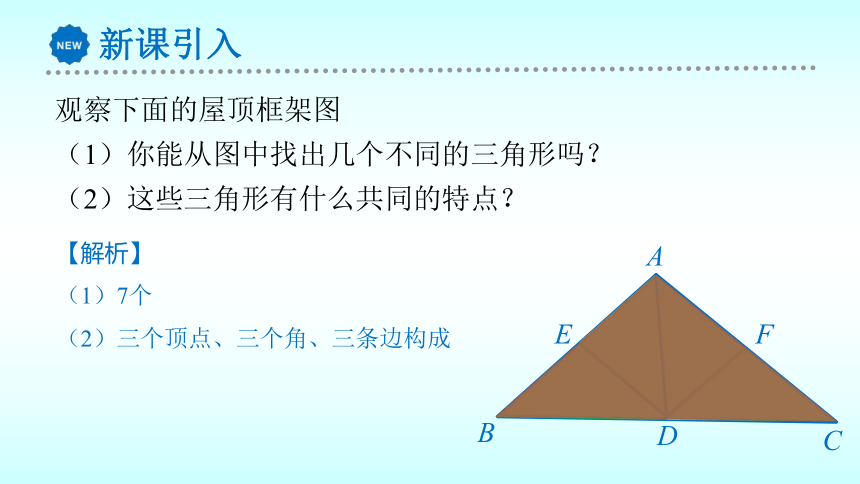
观察下面的屋顶框架图
(1)你能从图中找出几个不同的三角形吗?
(2)这些三角形有什么共同的特点?
A
B
C
E
F
D
【解析】
(1)7个
(2)三个顶点、三个角、三条边构成
观察下面的屋顶框架图
(1)你能从图中找出几个不同的三角形吗?
(2)这些三角形有什么共同的特点?
新课引入
讲授新知
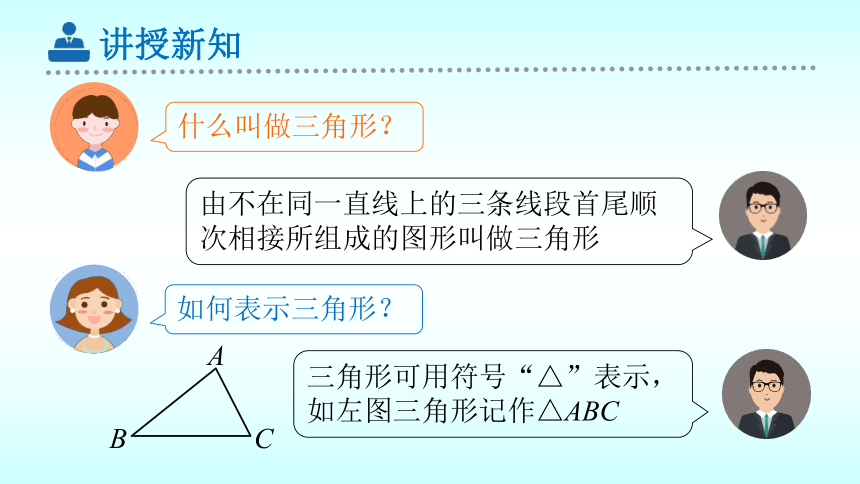
什么叫做三角形?
由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形
如何表示三角形?
三角形可用符号“△”表示,如左图三角形记作△ABC
A
B
C
三角形的边可以怎么表示?
方法一:可用一个小写字母表示.
方法二:可用顶点的两个大写字母表示.
A
B
C
c
a
b
如图三角形中三边可表示为AB,BC,AC
也可以表示为c,a,b
讲授新知
三角形的三要素是顶点、角和边
如果说三角形有三要素,
是哪三要素呢?
A
B
C
c
a
b
顶点:三角形中有3个顶点,顶点A,顶点B,顶点C
角:三角形中有3个角,∠A,∠B,∠C
边:三角形中有3条边,
AB,BC,AC
讲授新知
例1.
如图,思考回答下列问题
(1)图中共有几个不同的三角形?分别表示一下;
(2)以AD为边的三角形有________;
(3)在△ABD、△ABE、△ABC中∠B的对边分别是____.
【解析】
(1)6个;△ABD、△ADE、△ACE、
△ABE、△ADC、
△ABC
(2)△ABD、△ADE、△ACD
(3)AD、AE、AC
A
B
D
E
C
例题精讲
三角形的三个内角和是180°
请你进一步用学过的知识解释一下“三角形的三个内角和是180?”吗
我可以操作演示
三角形的三个内角和是多少?
探索新知
可以,我再试试
这个方法是小学的方法,需要撕下两个角,能不能只撕下一个角证明?
探索新知
我可以用平行线的知识来证明
还有其他的方法吗?不撕三角形的角
这个我得想想
探索新知
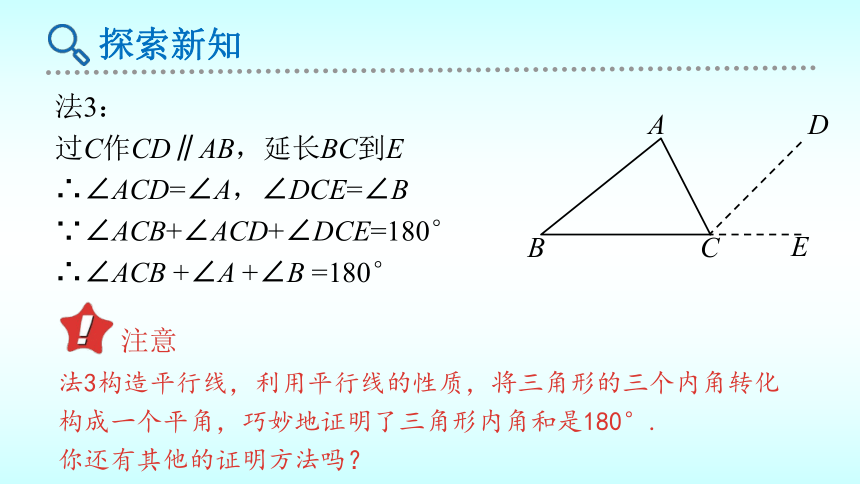
法3:
过C作CD∥AB,延长BC到E
∴∠ACD=∠A,∠DCE=∠B
∵∠ACB+∠ACD+∠DCE=180°
∴∠ACB
+∠A
+∠B
=180°
A
B
E
D
C
法3构造平行线,利用平行线的性质,将三角形的三个内角转化
构成一个平角,巧妙地证明了三角形内角和是180°.
你还有其他的证明方法吗?
注意
探索新知
三角形三个内角的和等于180
?
三角形的角还有其他性质吗?
讲授新知
探索新知
下面我们来玩一个游戏
如下图,有三个三角形,它们的两个内角被挡住了,你能判断出被挡住的角是什么角吗?
探索新知
下面我们来玩一个游戏
如下图,有三个三角形,它们的两个内角被挡住了,你能判断出被挡住的角是什么角吗?
探索新知
下面我们来玩一个游戏
如下图,有三个三角形,它们的两个内角被挡住了,你能判断出被挡住的角是什么角吗?
探索新知
探索新知
锐角三角形
(三个锐角)
探索新知
锐角三角形
(三个锐角)
直角三角形
(一个直角、两个锐角)
探索新知
直角三角形
(一个直角、两个锐角)
锐角三角形
(三个锐角)
钝角三角形
(一个钝角、两个锐角)
讲授新知
三角形按角的大小分类
三角形的分类
锐角三角形
三个内角都是锐角
钝角三角形
有一个内角是直角
直角三角形
有一个内角是钝角
+两个锐角
+两个锐角
1.
常用符号“Rt△ABC”来表示“直角三角形ABC”
把直角所对的边称为直角三角形的斜边;
夹直角的两条边称为直角边.
2.
直角三角形的两个锐角之间有什么关系?
直角三角形的两个锐角互余
讲授新知
我们来深入认识一下直角三角形
直角边
直角边
斜
边
A
B
C
1.
在△ABC中,∠A=80°,∠B=∠C,求∠C度数.
2.
如图,求△ABC的各内角的度数
3.
已知三角形三个内角的度数之比为1:3:5,求这三个内角的度数.
A
C
B
3x
2x
x
巩固练习1
1.
在△ABC中,∠A=80°,∠B=∠C,求∠C度数.
∵∠A+∠B+∠C=180°,∠A=80°,∠B=∠C
∴∠B+∠C=100°
∴∠C=50°
2.
如图,求△ABC的各内角的度数
∵∠A+∠B+∠C=180°
∴3x+2x+x=180
x=30
∴∠A=90°,∠B=60°,∠C=30°
A
C
B
3x
2x
x
巩固练习1
3.
已知三角形三个内角的度数之比为1:3:5,求这三个内角的度数.
设这三个内角分别为x,3x和5x
x+3x+5x=180
x=20
答:这三个角分别为20°,60°和100°
解法总结:结合方程思想,设每一份为x,利用内角和列方程
巩固练习1
1.
一个三角形的两个内角的度数分别如下,这个三角形是什么三角形?
(1)30°和
60°
(2)40°和
70°
(3)50°和
20°
2.如右图,∠ACB=90°,CD⊥AB,垂足是D.
(1)图中有几个直角三角形?是哪几个?分别说出它的直角边和斜边.
(2)∠1和∠A有什么关系?∠2和∠A呢?
C
B
A
D
2
1
巩固练习2
1.
一个三角形的两个内角的度数分别如下,这个三角形是什么三角形?
(1)30°和
60°
(2)40°和
70°
(3)50°和
20°
(1)30°、60°、90°:直角三角形
(2)40°、70°、70°:锐角三角形
(3)50°、20°、110°:钝角三角形
巩固练习2
2.如右图,∠ACB=90°,CD⊥AB,垂足是D.
(1)图中有几个直角三角形?是哪几个?分别说出它的直角边和斜边.
(2)∠1和∠A有什么关系?∠2和∠A呢?
(1)3个直角三角形
Rt△ABC:直角边AC、BC,斜边AB
Rt△ACD:直角边AD、CD,斜边AC
Rt△BCD:直角边CD、BD,斜边BC
C
B
A
D
2
1
巩固练习2
2.如右图,∠ACB=90°,CD⊥AB,垂足是D.
(1)图中有几个直角三角形?是哪几个?分别说出它的直角边和斜边.
(2)∠1和∠A有什么关系?∠2和∠A呢?
(2)∵CD⊥AB
∴∠ADC=90°
∴∠1和∠A互余
∵∠ACB=90°
∴∠1和∠2互余
C
B
A
D
2
1
巩固练习2
∴∠A=∠2
本课小结
作业布置
4.1
认识三角形
(第1
课时)
新课引入
观察下面的屋顶框架图
(1)你能从图中找出几个不同的三角形吗?
(2)这些三角形有什么共同的特点?
A
B
C
E
F
D
【解析】
(1)7个
(2)三个顶点、三个角、三条边构成
观察下面的屋顶框架图
(1)你能从图中找出几个不同的三角形吗?
(2)这些三角形有什么共同的特点?
新课引入
讲授新知
什么叫做三角形?
由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形
如何表示三角形?
三角形可用符号“△”表示,如左图三角形记作△ABC
A
B
C
三角形的边可以怎么表示?
方法一:可用一个小写字母表示.
方法二:可用顶点的两个大写字母表示.
A
B
C
c
a
b
如图三角形中三边可表示为AB,BC,AC
也可以表示为c,a,b
讲授新知
三角形的三要素是顶点、角和边
如果说三角形有三要素,
是哪三要素呢?
A
B
C
c
a
b
顶点:三角形中有3个顶点,顶点A,顶点B,顶点C
角:三角形中有3个角,∠A,∠B,∠C
边:三角形中有3条边,
AB,BC,AC
讲授新知
例1.
如图,思考回答下列问题
(1)图中共有几个不同的三角形?分别表示一下;
(2)以AD为边的三角形有________;
(3)在△ABD、△ABE、△ABC中∠B的对边分别是____.
【解析】
(1)6个;△ABD、△ADE、△ACE、
△ABE、△ADC、
△ABC
(2)△ABD、△ADE、△ACD
(3)AD、AE、AC
A
B
D
E
C
例题精讲
三角形的三个内角和是180°
请你进一步用学过的知识解释一下“三角形的三个内角和是180?”吗
我可以操作演示
三角形的三个内角和是多少?
探索新知
可以,我再试试
这个方法是小学的方法,需要撕下两个角,能不能只撕下一个角证明?
探索新知
我可以用平行线的知识来证明
还有其他的方法吗?不撕三角形的角
这个我得想想
探索新知
法3:
过C作CD∥AB,延长BC到E
∴∠ACD=∠A,∠DCE=∠B
∵∠ACB+∠ACD+∠DCE=180°
∴∠ACB
+∠A
+∠B
=180°
A
B
E
D
C
法3构造平行线,利用平行线的性质,将三角形的三个内角转化
构成一个平角,巧妙地证明了三角形内角和是180°.
你还有其他的证明方法吗?
注意
探索新知
三角形三个内角的和等于180
?
三角形的角还有其他性质吗?
讲授新知
探索新知
下面我们来玩一个游戏
如下图,有三个三角形,它们的两个内角被挡住了,你能判断出被挡住的角是什么角吗?
探索新知
下面我们来玩一个游戏
如下图,有三个三角形,它们的两个内角被挡住了,你能判断出被挡住的角是什么角吗?
探索新知
下面我们来玩一个游戏
如下图,有三个三角形,它们的两个内角被挡住了,你能判断出被挡住的角是什么角吗?
探索新知
探索新知
锐角三角形
(三个锐角)
探索新知
锐角三角形
(三个锐角)
直角三角形
(一个直角、两个锐角)
探索新知
直角三角形
(一个直角、两个锐角)
锐角三角形
(三个锐角)
钝角三角形
(一个钝角、两个锐角)
讲授新知
三角形按角的大小分类
三角形的分类
锐角三角形
三个内角都是锐角
钝角三角形
有一个内角是直角
直角三角形
有一个内角是钝角
+两个锐角
+两个锐角
1.
常用符号“Rt△ABC”来表示“直角三角形ABC”
把直角所对的边称为直角三角形的斜边;
夹直角的两条边称为直角边.
2.
直角三角形的两个锐角之间有什么关系?
直角三角形的两个锐角互余
讲授新知
我们来深入认识一下直角三角形
直角边
直角边
斜
边
A
B
C
1.
在△ABC中,∠A=80°,∠B=∠C,求∠C度数.
2.
如图,求△ABC的各内角的度数
3.
已知三角形三个内角的度数之比为1:3:5,求这三个内角的度数.
A
C
B
3x
2x
x
巩固练习1
1.
在△ABC中,∠A=80°,∠B=∠C,求∠C度数.
∵∠A+∠B+∠C=180°,∠A=80°,∠B=∠C
∴∠B+∠C=100°
∴∠C=50°
2.
如图,求△ABC的各内角的度数
∵∠A+∠B+∠C=180°
∴3x+2x+x=180
x=30
∴∠A=90°,∠B=60°,∠C=30°
A
C
B
3x
2x
x
巩固练习1
3.
已知三角形三个内角的度数之比为1:3:5,求这三个内角的度数.
设这三个内角分别为x,3x和5x
x+3x+5x=180
x=20
答:这三个角分别为20°,60°和100°
解法总结:结合方程思想,设每一份为x,利用内角和列方程
巩固练习1
1.
一个三角形的两个内角的度数分别如下,这个三角形是什么三角形?
(1)30°和
60°
(2)40°和
70°
(3)50°和
20°
2.如右图,∠ACB=90°,CD⊥AB,垂足是D.
(1)图中有几个直角三角形?是哪几个?分别说出它的直角边和斜边.
(2)∠1和∠A有什么关系?∠2和∠A呢?
C
B
A
D
2
1
巩固练习2
1.
一个三角形的两个内角的度数分别如下,这个三角形是什么三角形?
(1)30°和
60°
(2)40°和
70°
(3)50°和
20°
(1)30°、60°、90°:直角三角形
(2)40°、70°、70°:锐角三角形
(3)50°、20°、110°:钝角三角形
巩固练习2
2.如右图,∠ACB=90°,CD⊥AB,垂足是D.
(1)图中有几个直角三角形?是哪几个?分别说出它的直角边和斜边.
(2)∠1和∠A有什么关系?∠2和∠A呢?
(1)3个直角三角形
Rt△ABC:直角边AC、BC,斜边AB
Rt△ACD:直角边AD、CD,斜边AC
Rt△BCD:直角边CD、BD,斜边BC
C
B
A
D
2
1
巩固练习2
2.如右图,∠ACB=90°,CD⊥AB,垂足是D.
(1)图中有几个直角三角形?是哪几个?分别说出它的直角边和斜边.
(2)∠1和∠A有什么关系?∠2和∠A呢?
(2)∵CD⊥AB
∴∠ADC=90°
∴∠1和∠A互余
∵∠ACB=90°
∴∠1和∠2互余
C
B
A
D
2
1
巩固练习2
∴∠A=∠2
本课小结
作业布置
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
