鲁教版(五四制)八年级数学下册第九章 图形的相似 单元练习(含答案)
文档属性
| 名称 | 鲁教版(五四制)八年级数学下册第九章 图形的相似 单元练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 418.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-29 07:31:19 | ||
图片预览

文档简介
第九章
图形的相似
一、单选题
1.已知2x=3y,则下列比例式成立的是( )
A.
B.
C.
D.
2.如图,已知,那么下列结论正确的是(
)
A.
B.
C.
D.
3.下列说法正确的是(
)
A.矩形都是相似图形;
B.菱形都是相似图形
C.各边对应成比例的多边形是相似多边形;
D.等边三角形都是相似三角形
4.如图,点、分别在的、边上,增加下列哪些条件:①;②;③,使与一定相似(
)
A.①③
B.②③
C.①②
D.①②③
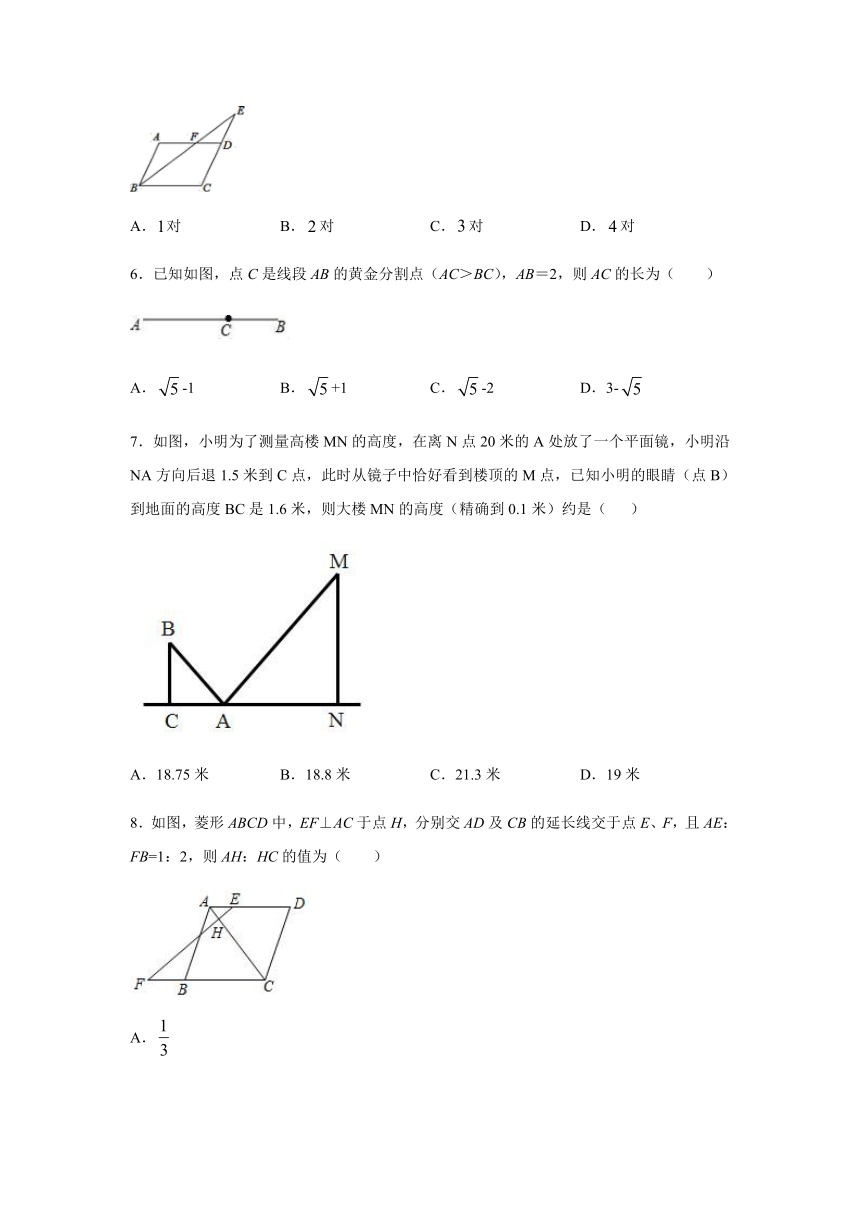
5.如图,平行四边形中,是的延长线上一点,与交于点,则图中的相似三角形对数共有(
)
A.对
B.对
C.对
D.对
6.已知如图,点C是线段AB的黄金分割点(AC>BC),AB=2,则AC的长为( )
A.-1
B.+1
C.-2
D.3-
7.如图,小明为了测量高楼MN的高度,在离N点20米的A处放了一个平面镜,小明沿NA方向后退1.5米到C点,此时从镜子中恰好看到楼顶的M点,已知小明的眼睛(点B)到地面的高度BC是1.6米,则大楼MN的高度(精确到0.1米)约是(
)
A.18.75米
B.18.8米
C.21.3米
D.19米
8.如图,菱形ABCD中,EF⊥AC于点H,分别交AD及CB的延长线交于点E、F,且AE:FB=1:2,则AH:HC的值为( )
A.
B.
C.
D.
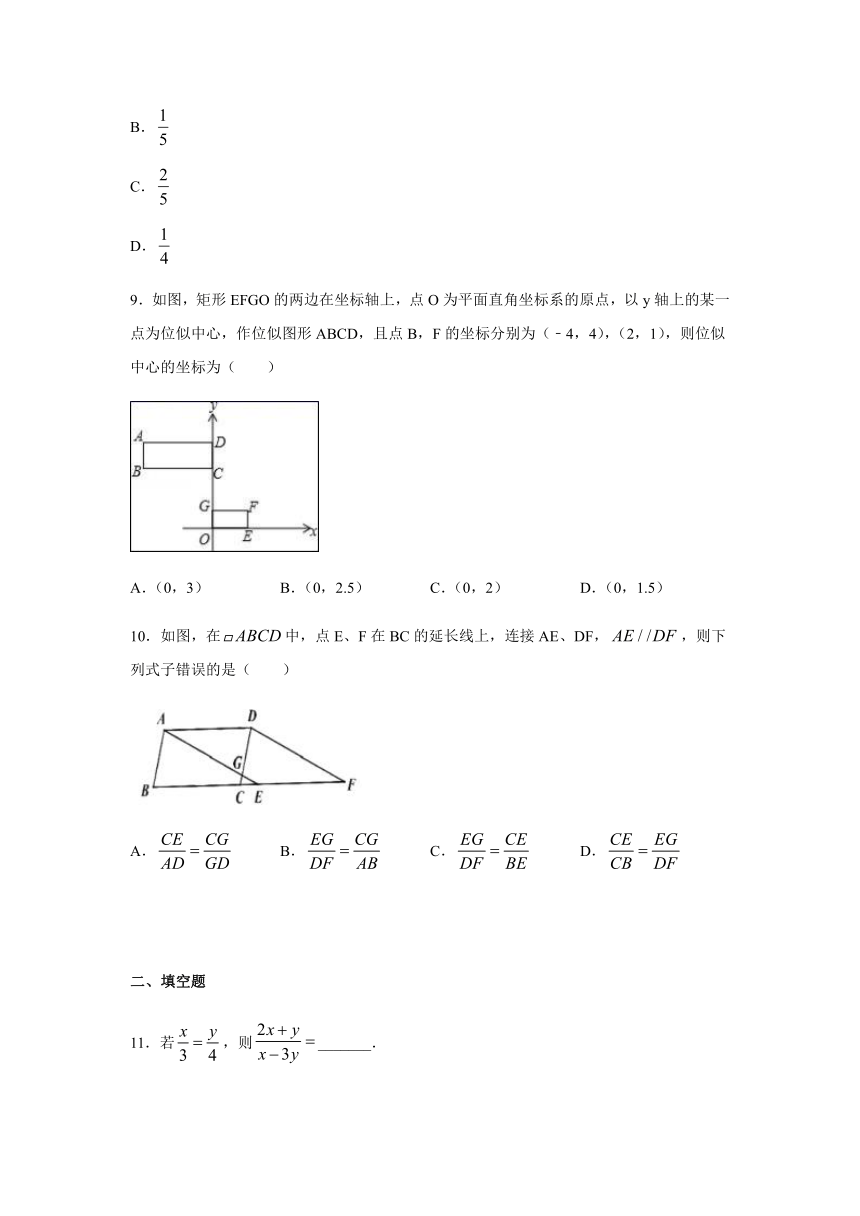
9.如图,矩形EFGO的两边在坐标轴上,点O为平面直角坐标系的原点,以y轴上的某一点为位似中心,作位似图形ABCD,且点B,F的坐标分别为(﹣4,4),(2,1),则位似中心的坐标为( )
A.(0,3)
B.(0,2.5)
C.(0,2)
D.(0,1.5)
10.如图,在中,点E、F在BC的延长线上,连接AE、DF,,则下列式子错误的是(
)
A.
B.
C.
D.
二、填空题
11.若,则_______.
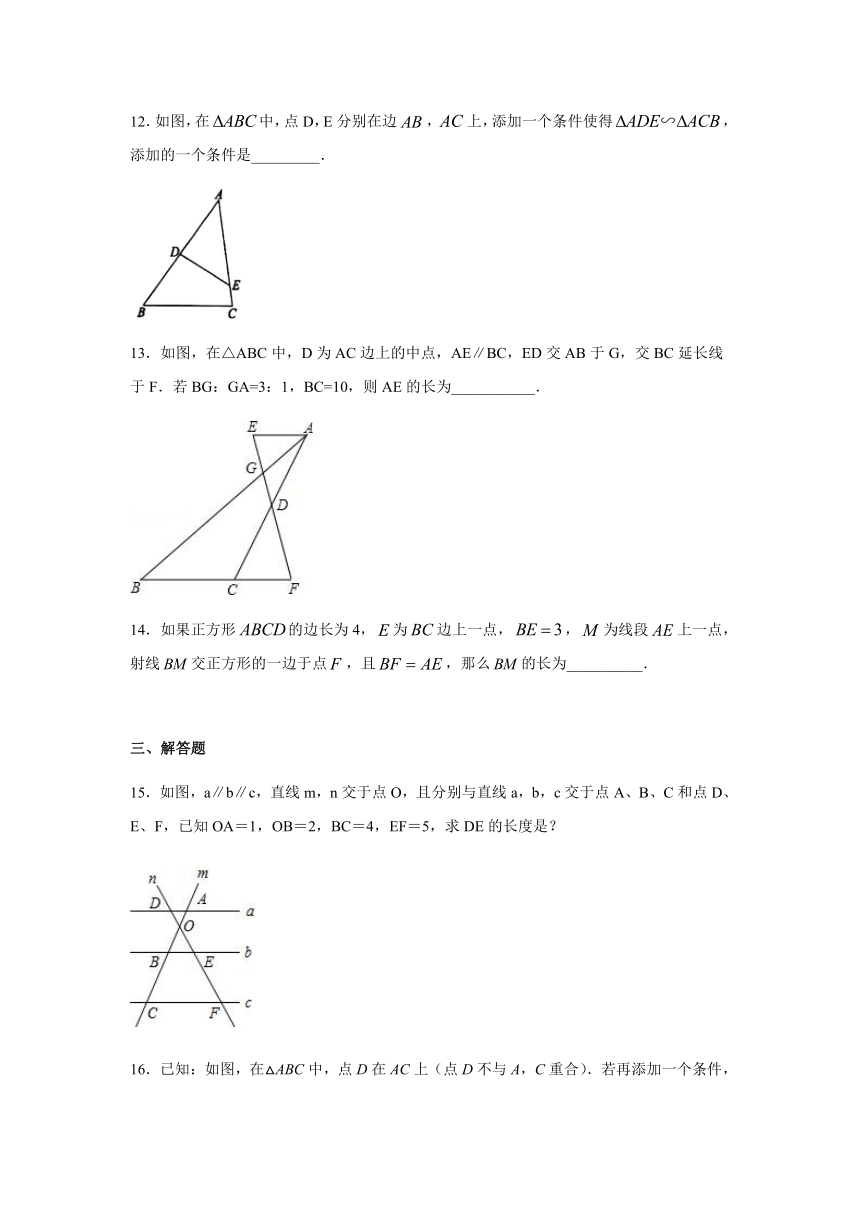
12.如图,在中,点D,E分别在边,上,添加一个条件使得,添加的一个条件是_________.
13.如图,在△ABC中,D为AC边上的中点,AE∥BC,ED交AB于G,交BC延长线于F.若BG:GA=3:1,BC=10,则AE的长为___________.
14.如果正方形的边长为4,为边上一点,,为线段上一点,射线交正方形的一边于点,且,那么的长为__________.
三、解答题
15.如图,a∥b∥c,直线m,n交于点O,且分别与直线a,b,c交于点A、B、C和点D、E、F,已知OA=1,OB=2,BC=4,EF=5,求DE的长度是?
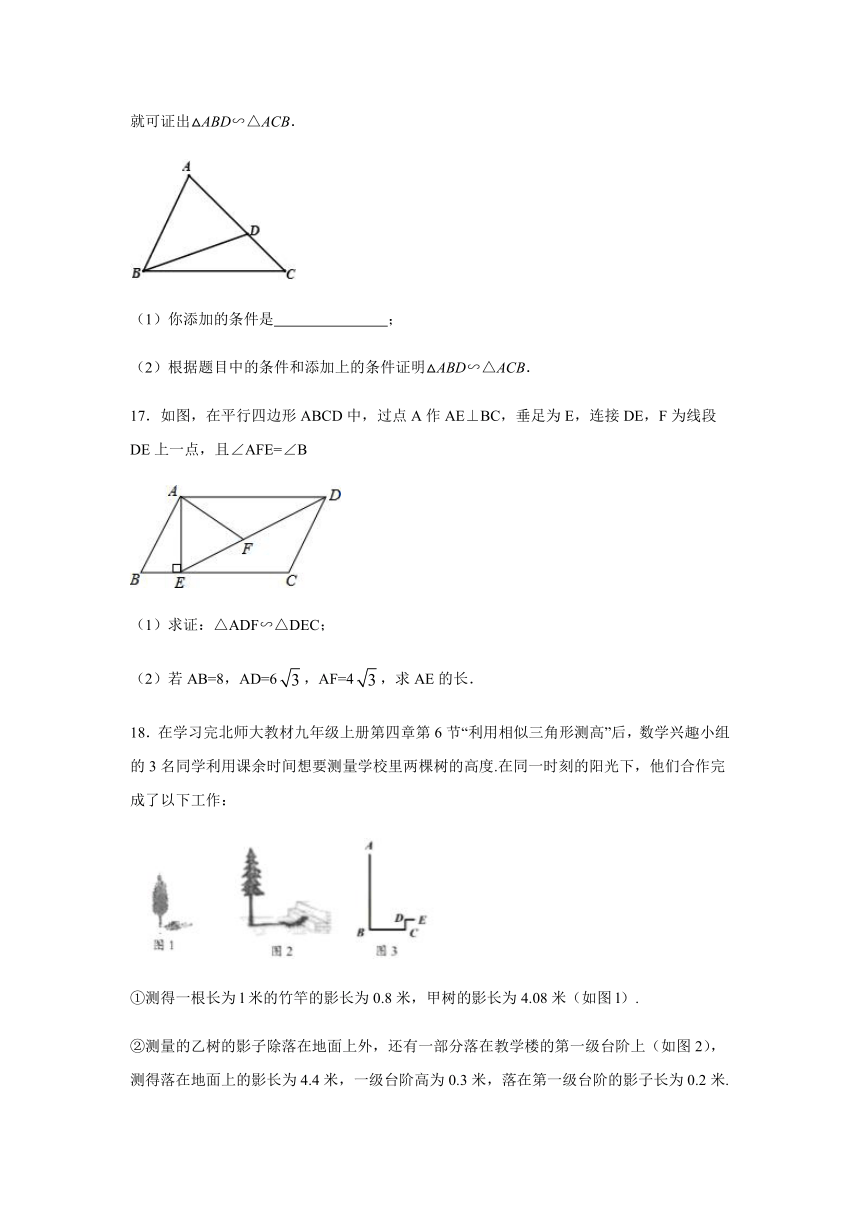
16.已知:如图,在△ABC中,点D在AC上(点D不与A,C重合).若再添加一个条件,就可证出△ABD∽△ACB.
(1)你添加的条件是
;
(2)根据题目中的条件和添加上的条件证明△ABD∽△ACB.
17.如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6,AF=4,求AE的长.
18.在学习完北师大教材九年级上册第四章第6节“利用相似三角形测高”后,数学兴趣小组的3名同学利用课余时间想要测量学校里两棵树的高度.在同一时刻的阳光下,他们合作完成了以下工作:
①测得一根长为l米的竹竿的影长为0.8米,甲树的影长为4.08米(如图l).
②测量的乙树的影子除落在地面上外,还有一部分落在教学楼的第一级台阶上(如图2),测得落在地面上的影长为4.4米,一级台阶高为0.3米,落在第一级台阶的影子长为0.2米.
(1)在横线上直接填写甲树的高度为_____________米.
(2)图3为图2的示意图,请利用图3求出乙树的高度
答案
1.C
2.A
3.D
4.A
5.C
6.A
7.C
8.B
9.C
10.D
11..
12.∠ADE=∠ACB
13.5
14.或
15.解:∵OA=1,OB=2,
∴AB=3,
∵a∥b∥c,
∴,
即,
∴;
∴DE的长度是.
16.(1)∵△ABD与△ACB有一公共角∠A,
∴当∠ABD=∠C时,△ABD∽△ACB,
或∠ADB=∠ABC时,△ABD∽△ACB,
或时,△ABD∽△ACB,
故答案为:∠ABD=∠C(或∠ADB=∠ABC或,答案不唯一);
(2)∵∠ABD=∠C,∠A=∠A,
∴△ABD∽△ACB;
∵∠ADB=∠ABC,∠A=∠A
∴△ABD∽△ACB;
∵,∠A=∠A,
∴△ABD∽△ACB.
17.解:(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC
∴∠C+∠B=180°,∠ADF=∠DEC
∵∠AFD+∠AFE=180°,∠AFE=∠B,
∴∠AFD=∠C
在△ADF与△DEC中,∵∠AFD=∠C,∠ADF=∠DEC,
∴△ADF∽△DEC
(2)∵四边形ABCD是平行四边形,
∴CD=AB=8.
由(1)知△ADF∽△DEC,
∴,
∴
在Rt△ADE中,由勾股定理得:
18.解:(1)设甲树的高度为x米,根据题意得,
,
解得,x=5.1
∴甲树的高度为5.1米.
(2)如图,过D作DF⊥AB,垂足为F,则∠DFB=∠FBC=∠BCD=90°,
∴四边形DFBC是矩形,
∴DF=BC=4.4米,BF=CD=0.3米,
∴EF=4.4+0.2=4.6米,
根据题意得,
,
解得,AF=5.75米,
∴AB=5.75+0.3=6.05米.
答:乙树的高度是6.05米.
图形的相似
一、单选题
1.已知2x=3y,则下列比例式成立的是( )
A.
B.
C.
D.
2.如图,已知,那么下列结论正确的是(
)
A.
B.
C.
D.
3.下列说法正确的是(
)
A.矩形都是相似图形;
B.菱形都是相似图形
C.各边对应成比例的多边形是相似多边形;
D.等边三角形都是相似三角形
4.如图,点、分别在的、边上,增加下列哪些条件:①;②;③,使与一定相似(
)
A.①③
B.②③
C.①②
D.①②③
5.如图,平行四边形中,是的延长线上一点,与交于点,则图中的相似三角形对数共有(
)
A.对
B.对
C.对
D.对
6.已知如图,点C是线段AB的黄金分割点(AC>BC),AB=2,则AC的长为( )
A.-1
B.+1
C.-2
D.3-
7.如图,小明为了测量高楼MN的高度,在离N点20米的A处放了一个平面镜,小明沿NA方向后退1.5米到C点,此时从镜子中恰好看到楼顶的M点,已知小明的眼睛(点B)到地面的高度BC是1.6米,则大楼MN的高度(精确到0.1米)约是(
)
A.18.75米
B.18.8米
C.21.3米
D.19米
8.如图,菱形ABCD中,EF⊥AC于点H,分别交AD及CB的延长线交于点E、F,且AE:FB=1:2,则AH:HC的值为( )
A.
B.
C.
D.
9.如图,矩形EFGO的两边在坐标轴上,点O为平面直角坐标系的原点,以y轴上的某一点为位似中心,作位似图形ABCD,且点B,F的坐标分别为(﹣4,4),(2,1),则位似中心的坐标为( )
A.(0,3)
B.(0,2.5)
C.(0,2)
D.(0,1.5)
10.如图,在中,点E、F在BC的延长线上,连接AE、DF,,则下列式子错误的是(
)
A.
B.
C.
D.
二、填空题
11.若,则_______.
12.如图,在中,点D,E分别在边,上,添加一个条件使得,添加的一个条件是_________.
13.如图,在△ABC中,D为AC边上的中点,AE∥BC,ED交AB于G,交BC延长线于F.若BG:GA=3:1,BC=10,则AE的长为___________.
14.如果正方形的边长为4,为边上一点,,为线段上一点,射线交正方形的一边于点,且,那么的长为__________.
三、解答题
15.如图,a∥b∥c,直线m,n交于点O,且分别与直线a,b,c交于点A、B、C和点D、E、F,已知OA=1,OB=2,BC=4,EF=5,求DE的长度是?
16.已知:如图,在△ABC中,点D在AC上(点D不与A,C重合).若再添加一个条件,就可证出△ABD∽△ACB.
(1)你添加的条件是
;
(2)根据题目中的条件和添加上的条件证明△ABD∽△ACB.
17.如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6,AF=4,求AE的长.
18.在学习完北师大教材九年级上册第四章第6节“利用相似三角形测高”后,数学兴趣小组的3名同学利用课余时间想要测量学校里两棵树的高度.在同一时刻的阳光下,他们合作完成了以下工作:
①测得一根长为l米的竹竿的影长为0.8米,甲树的影长为4.08米(如图l).
②测量的乙树的影子除落在地面上外,还有一部分落在教学楼的第一级台阶上(如图2),测得落在地面上的影长为4.4米,一级台阶高为0.3米,落在第一级台阶的影子长为0.2米.
(1)在横线上直接填写甲树的高度为_____________米.
(2)图3为图2的示意图,请利用图3求出乙树的高度
答案
1.C
2.A
3.D
4.A
5.C
6.A
7.C
8.B
9.C
10.D
11..
12.∠ADE=∠ACB
13.5
14.或
15.解:∵OA=1,OB=2,
∴AB=3,
∵a∥b∥c,
∴,
即,
∴;
∴DE的长度是.
16.(1)∵△ABD与△ACB有一公共角∠A,
∴当∠ABD=∠C时,△ABD∽△ACB,
或∠ADB=∠ABC时,△ABD∽△ACB,
或时,△ABD∽△ACB,
故答案为:∠ABD=∠C(或∠ADB=∠ABC或,答案不唯一);
(2)∵∠ABD=∠C,∠A=∠A,
∴△ABD∽△ACB;
∵∠ADB=∠ABC,∠A=∠A
∴△ABD∽△ACB;
∵,∠A=∠A,
∴△ABD∽△ACB.
17.解:(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC
∴∠C+∠B=180°,∠ADF=∠DEC
∵∠AFD+∠AFE=180°,∠AFE=∠B,
∴∠AFD=∠C
在△ADF与△DEC中,∵∠AFD=∠C,∠ADF=∠DEC,
∴△ADF∽△DEC
(2)∵四边形ABCD是平行四边形,
∴CD=AB=8.
由(1)知△ADF∽△DEC,
∴,
∴
在Rt△ADE中,由勾股定理得:
18.解:(1)设甲树的高度为x米,根据题意得,
,
解得,x=5.1
∴甲树的高度为5.1米.
(2)如图,过D作DF⊥AB,垂足为F,则∠DFB=∠FBC=∠BCD=90°,
∴四边形DFBC是矩形,
∴DF=BC=4.4米,BF=CD=0.3米,
∴EF=4.4+0.2=4.6米,
根据题意得,
,
解得,AF=5.75米,
∴AB=5.75+0.3=6.05米.
答:乙树的高度是6.05米.
