人教版数学七年级下册 9.1.2 不等式的性质课件(共25张PPT)
文档属性
| 名称 | 人教版数学七年级下册 9.1.2 不等式的性质课件(共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-29 00:00:00 | ||
图片预览






文档简介
(共28张PPT)
等式基本性质1:
等式的两边都加上(或减去)同一个整式,等式仍旧成立
等式基本性质2:
等式的两边都乘以(或除以)同一个不为0的数,等式仍旧成立
如果a=b,那么a±c=b±c
如果a=b,那么ac=bc或
(c≠0),
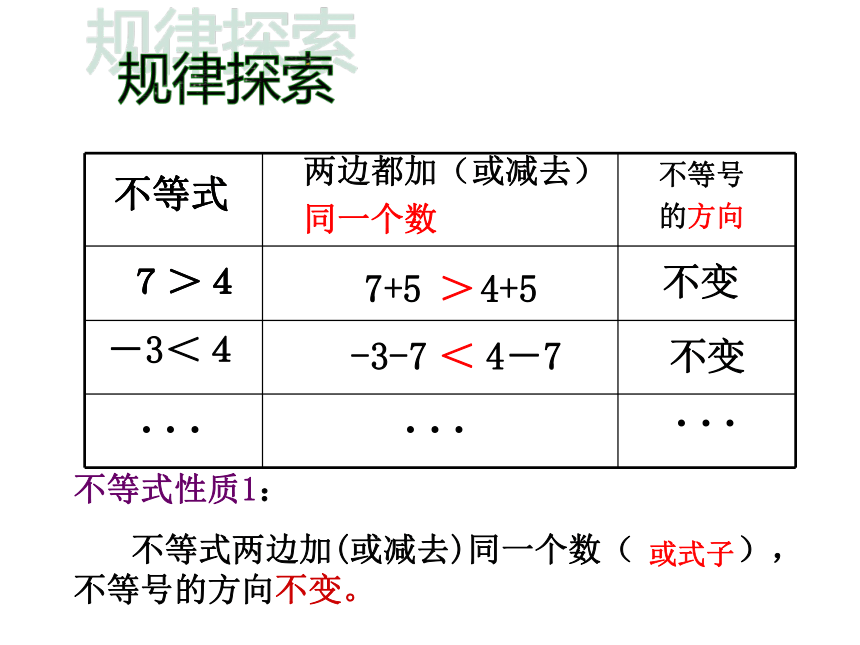
不等式
7>4
-3<4
7+5
4+5
-3-7
4-7
不变
不变
两边都加(或减去)
同一个数
不等式
7>4
...
...
...
不等式性质1:
不等式两边加(或减去)同一个数(
),不等号的方向不变。
或式子
>
<
不等号
的方向
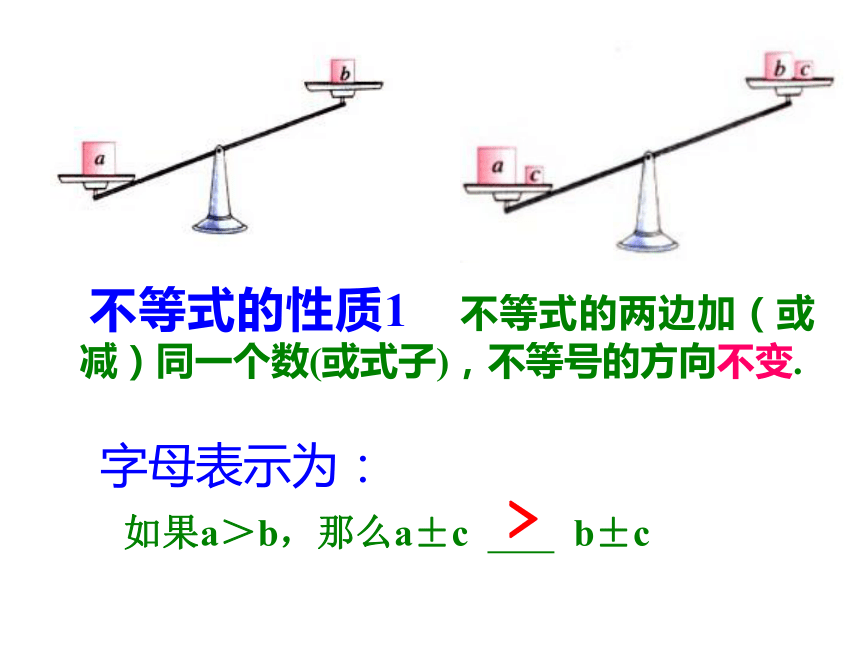
不等式的性质1
不等式的两边加(或减)同一个数(或式子),不等号的方向不变.
如果a>b,那么a±c
b±c
字母表示为:
﹥
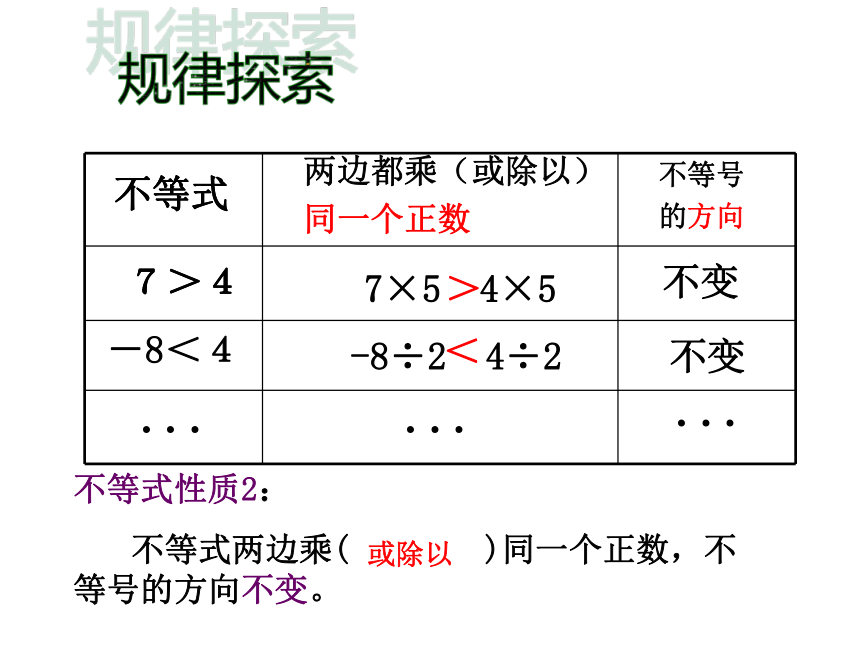
不等式
7>4
-8<4
7×5
4×5
-8÷2
4÷2
不变
不变
两边都乘(或除以)
同一个正数
不等式
7>4
...
...
...
不等式性质2:
不等式两边乘(
)同一个正数,不等号的方向不变。
或除以
>
<
不等号
的方向
不等式的性质2
不等式的两边乘(或除以)同一个正数,不等号的方向不变.
如果a<b,c>0那么ac
bc,
字母表示为:
﹤
﹤
不等式
7>4
-8<4
7×(-5)
4×(-5)
-8÷(-2)
4÷(-2)
改变
改变
两边都乘(或除以)
同一个负数
不等式
7>4
...
...
...
不等式性质3:
不等式两边乘(
)同一个负数,不等号的方向改变。
或除以
<
>
不等号
的方向
不等式的性质
3
不等式的两边乘(或除以)同一个负数,不等号的方向改变
必须把不等号的方向改变
如果a>b,c<0那么ac
bc,
字母表示为:
类比推导
﹤
﹤
不等式性质1:
不等式两边加(
减去
)同一个正数,不等号的方向不变。
不等式性质2:
不等式两边乘(
或除以
)同一个正数,不等号的方向不变。
不等式性质3:
不等式两边乘(
或除以
)同一个负数,不等号的方向改变。
针对练习
(1)如果x-5>4,那么两边都
可得到x>9
(2)如果在-7<8的两边都加上9可得到
(3)如果在5>-2的两边都加上a+2可得到
(4)如果在-3>-4的两边都乘以7可得到
(5)如果在8>0的两边都乘以8可得到
(6)如果在
的两边都乘以14
可得到
加上5
2
<
17
a+7
>
a
-21>-28
64
>
0
2x>28+7x
(1)如果在不等式8>0的两边都乘以―8可得到
(2)如果-3x>9,那么两边都除以―3可得到
(3)设m>n,用“>”或“<”填空:
m-5
n-5(根据不等式的性质
)
-6m
-6n(根据不等式的性质
)
-64
<
0
x
<
-3
>
1
<
3
例1:
?判断下列各题的推导是否正确?为什么(学生口答)
(1)因为7.5>5.7,所以-7.5<-5.7;
(2)因为a+8>4,所以a>-4;
(3)因为4a>4b,所以a>b;
(4)因为-1>-2,所以-a-1>-a-2;
(5)因为3>2,所以3a>2a.
答:
.
(1)正确,根据不等式基本性质3.
(2)正确,根据不等式基本性质1.
(3)正确,根据不等式基本性质2.
(4)正确,根据不等式基本性质1.
(5)不对,应分情况逐一讨论.
当a>0时,3a>2a.(不等式基本性质2)
当
a=0时,3a=2a.
当a<0时,3a<2a.(不等式基本性质3)
例2:设a>b,用“<”或“>”填空并口答是根据哪一条不等式基本性质。
(1)
a
-
3____b
-
3;
(2)a÷3____b÷3
(3)
0.1a____0.1b;
(4)
-4a____-4b
(5)
2a+3____2b+3;
(6)
(m2+1)
a
____
(m2+1)b
(m为常数)
>
>
>
>
>
<
练习:?已知a<0,用“<”或“>”号填空:
(1)a+2
____2;
?(2)a-1
_____-1;
(3)3a______
0;
(4)-a/4______0;
(5)a2_____0;
(6)a3______0
(7)a-1______0;??
(8)|a|______0.
答:
(1)a+2<2,根据不等式基本性质1.
(2)a-1<-1,根据不等式基本性质1.
(3)3a<0,根据不等式基本性质2.
(5)因为a<0,两边同乘以a<0,
由不等式基本性质3,得a2>0.
(6)因为a<0,两边同乘以a2>0,
由不等式基本性质2,得a3<0.
(7)因为a<0,两边同加上-1,由不等式基本性质1,
得a-1<-1.又已知,-1<0,所以
a-1<0.
(8)因为a<0,所以a≠0,所以|a|>0.
(4)
-a/4>0,根据不等式基本性质3.
(1)
(2)
(3)
(4)
(5)
1、
判断
(√)
(×)
(√)
(×)
(×)
2、判断正误:
(1)如果a>b,那么ac>bc。
(2)如果a>b,那么ac2>bc2。
(3)如果ac2>bc2,
那么a>b。
×
×
例3 利用不等式的性质解下列不等式.
(1)
x-7>26
(2)
-4x﹥3
(3)
3x<2x+1
Zx.xk
例1 利用不等式的性质解下列不等式用数轴表示解集.
(1)
x-7>26
解:根据不等式性质1,得
X-7+7>26+7
X>33
(2)
-4x﹥3
解:根据不等式性质3,得
(3)
3x<2x+1
3x-2x﹤2x+1-2x
x﹤1
这个不等式的解在数轴上的表示
注意:解不等式时也可以“移项”,即把不等式的一边的某项变号后移到另一边,而不改变不等号的方向.
解:根据不等式性质1,得
3x-2x﹤1
x﹥75
这个不等式的解集在数轴的表示如图
自我检测
利用不等式的性质解下列不等式用数轴表示解集.
(1)
x+3>-1
解:根据不等式性质1,得
X<-7
(3)
4x>-12
解:根据不等式性质2,得
X>-3
解:根据不等式性质1,得
X>-4
(2)
6x<5x-7
(5)
解:不等式两边同时乘以12,得
2(5x+1)-2×12>3(x-5)
10x+2-24>3x-15
10x-3x>24-2-15
7x>7
X>1
新情境题
以下不等式中,不等号用对了么?
(1)3-a<6-a
(2)3a<6a
解:(1)3<6,根据不等式的性质1
将不等式两边同时减a,3-a<6-a
(2)3<6,当a>0时,根据不等式的性质2,3a<6a
当a<0时,根据不等式的性质3,3a>6a
如果关于x的不等式
(1-a)x>1-a
的解
集为
x<1
,那么请给出一个符合题意a的值
解:由(1-a)x>1-a
,不等式两边同时除以
1-a
,得到
x<1
不等号方向改变了,由不等式的性质3可知
1-a<0,a>1
可以取a=2
等式基本性质1:
等式的两边都加上(或减去)同一个整式,等式仍旧成立
等式基本性质2:
等式的两边都乘以(或除以)同一个不为0的数,等式仍旧成立
如果a=b,那么a±c=b±c
如果a=b,那么ac=bc或
(c≠0),
不等式
7>4
-3<4
7+5
4+5
-3-7
4-7
不变
不变
两边都加(或减去)
同一个数
不等式
7>4
...
...
...
不等式性质1:
不等式两边加(或减去)同一个数(
),不等号的方向不变。
或式子
>
<
不等号
的方向
不等式的性质1
不等式的两边加(或减)同一个数(或式子),不等号的方向不变.
如果a>b,那么a±c
b±c
字母表示为:
﹥
不等式
7>4
-8<4
7×5
4×5
-8÷2
4÷2
不变
不变
两边都乘(或除以)
同一个正数
不等式
7>4
...
...
...
不等式性质2:
不等式两边乘(
)同一个正数,不等号的方向不变。
或除以
>
<
不等号
的方向
不等式的性质2
不等式的两边乘(或除以)同一个正数,不等号的方向不变.
如果a<b,c>0那么ac
bc,
字母表示为:
﹤
﹤
不等式
7>4
-8<4
7×(-5)
4×(-5)
-8÷(-2)
4÷(-2)
改变
改变
两边都乘(或除以)
同一个负数
不等式
7>4
...
...
...
不等式性质3:
不等式两边乘(
)同一个负数,不等号的方向改变。
或除以
<
>
不等号
的方向
不等式的性质
3
不等式的两边乘(或除以)同一个负数,不等号的方向改变
必须把不等号的方向改变
如果a>b,c<0那么ac
bc,
字母表示为:
类比推导
﹤
﹤
不等式性质1:
不等式两边加(
减去
)同一个正数,不等号的方向不变。
不等式性质2:
不等式两边乘(
或除以
)同一个正数,不等号的方向不变。
不等式性质3:
不等式两边乘(
或除以
)同一个负数,不等号的方向改变。
针对练习
(1)如果x-5>4,那么两边都
可得到x>9
(2)如果在-7<8的两边都加上9可得到
(3)如果在5>-2的两边都加上a+2可得到
(4)如果在-3>-4的两边都乘以7可得到
(5)如果在8>0的两边都乘以8可得到
(6)如果在
的两边都乘以14
可得到
加上5
2
<
17
a+7
>
a
-21>-28
64
>
0
2x>28+7x
(1)如果在不等式8>0的两边都乘以―8可得到
(2)如果-3x>9,那么两边都除以―3可得到
(3)设m>n,用“>”或“<”填空:
m-5
n-5(根据不等式的性质
)
-6m
-6n(根据不等式的性质
)
-64
<
0
x
<
-3
>
1
<
3
例1:
?判断下列各题的推导是否正确?为什么(学生口答)
(1)因为7.5>5.7,所以-7.5<-5.7;
(2)因为a+8>4,所以a>-4;
(3)因为4a>4b,所以a>b;
(4)因为-1>-2,所以-a-1>-a-2;
(5)因为3>2,所以3a>2a.
答:
.
(1)正确,根据不等式基本性质3.
(2)正确,根据不等式基本性质1.
(3)正确,根据不等式基本性质2.
(4)正确,根据不等式基本性质1.
(5)不对,应分情况逐一讨论.
当a>0时,3a>2a.(不等式基本性质2)
当
a=0时,3a=2a.
当a<0时,3a<2a.(不等式基本性质3)
例2:设a>b,用“<”或“>”填空并口答是根据哪一条不等式基本性质。
(1)
a
-
3____b
-
3;
(2)a÷3____b÷3
(3)
0.1a____0.1b;
(4)
-4a____-4b
(5)
2a+3____2b+3;
(6)
(m2+1)
a
____
(m2+1)b
(m为常数)
>
>
>
>
>
<
练习:?已知a<0,用“<”或“>”号填空:
(1)a+2
____2;
?(2)a-1
_____-1;
(3)3a______
0;
(4)-a/4______0;
(5)a2_____0;
(6)a3______0
(7)a-1______0;??
(8)|a|______0.
答:
(1)a+2<2,根据不等式基本性质1.
(2)a-1<-1,根据不等式基本性质1.
(3)3a<0,根据不等式基本性质2.
(5)因为a<0,两边同乘以a<0,
由不等式基本性质3,得a2>0.
(6)因为a<0,两边同乘以a2>0,
由不等式基本性质2,得a3<0.
(7)因为a<0,两边同加上-1,由不等式基本性质1,
得a-1<-1.又已知,-1<0,所以
a-1<0.
(8)因为a<0,所以a≠0,所以|a|>0.
(4)
-a/4>0,根据不等式基本性质3.
(1)
(2)
(3)
(4)
(5)
1、
判断
(√)
(×)
(√)
(×)
(×)
2、判断正误:
(1)如果a>b,那么ac>bc。
(2)如果a>b,那么ac2>bc2。
(3)如果ac2>bc2,
那么a>b。
×
×
例3 利用不等式的性质解下列不等式.
(1)
x-7>26
(2)
-4x﹥3
(3)
3x<2x+1
Zx.xk
例1 利用不等式的性质解下列不等式用数轴表示解集.
(1)
x-7>26
解:根据不等式性质1,得
X-7+7>26+7
X>33
(2)
-4x﹥3
解:根据不等式性质3,得
(3)
3x<2x+1
3x-2x﹤2x+1-2x
x﹤1
这个不等式的解在数轴上的表示
注意:解不等式时也可以“移项”,即把不等式的一边的某项变号后移到另一边,而不改变不等号的方向.
解:根据不等式性质1,得
3x-2x﹤1
x﹥75
这个不等式的解集在数轴的表示如图
自我检测
利用不等式的性质解下列不等式用数轴表示解集.
(1)
x+3>-1
解:根据不等式性质1,得
X<-7
(3)
4x>-12
解:根据不等式性质2,得
X>-3
解:根据不等式性质1,得
X>-4
(2)
6x<5x-7
(5)
解:不等式两边同时乘以12,得
2(5x+1)-2×12>3(x-5)
10x+2-24>3x-15
10x-3x>24-2-15
7x>7
X>1
新情境题
以下不等式中,不等号用对了么?
(1)3-a<6-a
(2)3a<6a
解:(1)3<6,根据不等式的性质1
将不等式两边同时减a,3-a<6-a
(2)3<6,当a>0时,根据不等式的性质2,3a<6a
当a<0时,根据不等式的性质3,3a>6a
如果关于x的不等式
(1-a)x>1-a
的解
集为
x<1
,那么请给出一个符合题意a的值
解:由(1-a)x>1-a
,不等式两边同时除以
1-a
,得到
x<1
不等号方向改变了,由不等式的性质3可知
1-a<0,a>1
可以取a=2
