人教版数学七年级下册 9.1.2 不等式的性质课件(2课时、共37张PPT)
文档属性
| 名称 | 人教版数学七年级下册 9.1.2 不等式的性质课件(2课时、共37张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-29 07:31:36 | ||
图片预览











文档简介
(共38张PPT)
第九章不等式与不等式组
9.1
不等式
在古代,我们的祖先就懂得了翘翘板的工作原理,并且根据这一原理设计出了一些简单机械,
并把它们用到了生活实践当中.
由此可见,“不相等”处处可见。
1.什么是等式?
2.等式的基本性质是什么?
等式的性质
等式的基本性质1:在等式两边都加上(或减去)同一个数或整式,结果仍相等.
如果a=b,那么a±c=b±c
等式的基本性质2:在等式两边都乘以或除以同一个数(除数不为0),结果仍相等.
如果a=b,那么ac=bc或
(c≠0),
不等式是否具有类似的性质呢?
探究一、请用”>””<”
填空并总结规律:
(1)5>3
,5+2
3+2,5-2
3-2
(2)-1<3,-1+2
3+2,-1-3
3-3
(3)6>2,6×5
2×5,
6×(-5)
2×(-5)
(4)-2<3,(-2)×6
3×6,
(-2)×(-6)
3×(-6)
>
>
<
<
>
<
>
<
由上面规律填空:
(1)当不等式两边加上或减去同一个数(正数或负数)时,不等号的方向
;
(2)当不等式两边乘同一个正数时,不等号的方向
;而乘同一个负数时,不等号的方向_________
不变
不变
改变
不等式基本性质1:不等式的两边都加上(或减去)同一个整式,
如果____,那么_________.
不等号的方向不变。
a>b
a±c>b±c
_________________
不等式基本性质2:不等式的两边都乘以(或除以)同一个____,不等号的方向____。
不等式基本性质3:不等式的两边都乘以(或除以)同一个____,不等号的方向____。
如果________,那么______________
不变
正数
a>b,c>0
ac>bc
(或
)
负数
改变
如果________,那么______________
a>b,c<0
ac(或
)
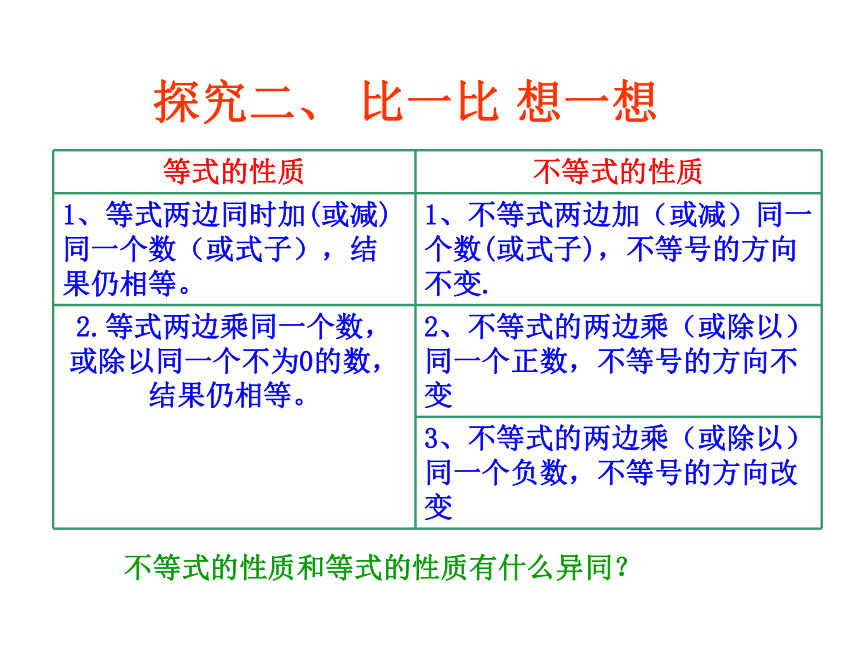
探究二、
比一比
想一想
不等式的性质和等式的性质有什么异同?
等式的性质
不等式的性质
1、等式两边同时加(或减)同一个数(或式子),结果仍相等。
1、不等式两边加(或减)同一个数(或式子),不等号的方向不变.
2.等式两边乘同一个数,或除以同一个不为0的数,结果仍相等。
2、不等式的两边乘(或除以)同一个正数,不等号的方向不变
3、不等式的两边乘(或除以)同一个负数,不等号的方向改变
不等式性质:
(1)不等式两边加(或减)同一个数(或式子),不等号的方向不变.
(2)不等式两边乘(或除以)同一个正数,不等号的方向不变.
(3)不等式两边乘(或除以)同一个负数,不等号的方向改变.
思考:(1)性质中的“不等号方向不变”和“不等号方向改变”的含义是什么?
(2)对比性质2和性质3,你能归纳出不等号的方向何时不变,何时改变吗?
若a>b,则
a±c>b±c
.
若a>b,则
a×c>b×c,
a÷c>
÷c
,(c>0)
若a>b,则
a×ca÷c÷c
,(c<0)
注意:
①在利用不等式的基本性质进行变形时,当不等式的两边都乘以(或除以)同一个字母,字母代表什么数是问题的关键,这决定了是用不等式基本性质2还是基本性质3,也就是不等号是否要改变方向的问题;
②运用不等式基本性质3时,要变两个号,一个性质符号,另一个是不等号.
探究三、补例:1
利用不等式的性质,填”>”,“<”
(1)若a>b,则2a+1
2b+1;
(2)若-1.25y<10,则y
-8;
(3)若a0,则ac+c
bc+c;
(4)若a>0,b<0,c<0,则(a-b)c
0.
>
>
<
<
解:(1)根据不等式基本性质1,两边都加上2,
得
x-2+2<3+2
x<5
(2)根据不等式基本性质1,两边都减去5x,
得
6x-5x<5x-1-5x
x<-1
解:(1)
∵a>b
∴两边都减去3,由不等式基本性质1
得
a-3>b-3
(2)
∵a>b,并且2>0
∴两边都除以2,由不等式基本性质2
得
(3)
∵a>b,并且-4<0
∴两边都乘以-4,由不等式基本性质3
得
-4a<-4b
不等式的基本性质1:
如果a
>b,那么a±c>b±c.就是说,不等式两边都加上
(或减去)同一个数(或式子),不等号方向不变。
不等式基本性质2:
如果a
>b,c
>
0
,那么
ac>bc(或
)
就是说不等式的两边都乘以(或除以)同一个正数,不等号的方向不变。
不等式基本性质3:
如果a>b,c<0
那么ac)就是说不等式的两边都乘以(或除以)同一个负数,不等号的方向改变。
1、(1)如果x-5>4,那么两边都
可得到x>9
(2)如果在-7<8的两边都加上9可得到
(3)如果在5>-2的两边都加上a+2可得到
(4)如果在-3>-4的两边都乘以7可得到
(5)如果在8>0的两边都乘以8可得到
(6)如果在
的两边都乘以14
可得到
加上5
2
<
17
a+7
>
a
-21>-28
64
>
0
2x>28+7x
2.用“>”或“<”在横线上填空,并在题后
括号内填写理由.若a
>
b;则
(1)
3a
3b;
(2)
a-8
b-8;
(3)
-2a
-2b;
(4)
2a-5
2b-5;
(5)
-3.5a-1
-3.5b-1.
>
>
<
<
>
不等式性质2
不等式性质1
不等式性质3
不等式性质1及2
不等式性质1及3
3、(1)如果在不等式8>0的两边都乘以―8可得到
(2)如果-3x>9,那么两边都除以-1/3可得到
(3)设m>n,用“>”或“<”填空:
m-5
n-5(根据不等式的性质
)
-6m
-6n(根据不等式的性质
)
-64
<
0
x
<
-3
>
1
<
3
4、判断正误:
(1)如果a>b,那么ac>bc。
(2)如果a>b,那么ac2>bc2。
(3)如果ac2>bc2,
那么a>b。
×
×
习
题
9.1
第4、6题
作业(课本P120)
第九章
不等式与不等式组
不等式基本性质1:不等式的两边都加上(或减去)同一个整式,
如果____,那么_________.
不等号的方向不变。
a>b
a±c>b±c
_________________
不等式基本性质2:不等式的两边都乘以(或除以)同一个____,不等号的方向____。
不等式基本性质3:不等式的两边都乘以(或除以)同一个____,不等号的方向____。
如果________,那么______________
不变
正数
a>b,c>0
ac>bc
(或
)
负数
改变
如果________,那么______________
a>b,c<0
ac(或
)
做一做:将下列不等式化成x
>
a或
x
<
a
的形式,并说出根据.
(1)
x-
7>26
(2)
3x
<
2x
+1
解:根据不等式的基本性质1
,
不等式两边都加上7,不等号方向不变,得,
x
>33
解:根据不等式的基本性质1,不等式两边都减去2x,不等号方向不变,得,
x
<
1
题目改为:利用不等式的性质解下列不等式,
并把解集在数轴上表示出来.
例1利用不等式的性质解下列不等式.
(1)
x-7>26
(2)
3x<2x+1
(3)
-
x﹥50 (4)
-
4x﹥3
3
2
探究一、
(1)
x-7>26
分析:解未知数为x的不等式,就是要使不等式逐步化为x﹥a或x﹤a的形式.
解:(1)为了使不等式x-7>26中不等号的一边变为x,根据不等式的性质1,不等式两边都加7,不等号的方向不变,得
x-7+7﹥26+7
x﹥33
这个不等式的解集在数轴上的表示如图,
(2)
3x<2x+1
3x-2x﹤2x+1-2x
x﹤1
为了使不等式3x<2x+1中不等号的一边变为x,根据
,不等式两边都减去
,不等号的方向
。
这个不等式的解在数轴上的表示如图
注意:解不等式时也可以“移项”,即把不等式的一边的某项变号后移到另一边,而不改变不等号的方向.
2x
不等式性质1
不变
得
x﹥75
这个不等式的解集在数轴的表示如图
不等式的两边都
除以2一3行吗?
(3)
x﹥50
(4)
-4x﹥3
为了使不等式-4x﹥3中的不等号的一边变为x,根据
,不等式两边都除以
,不等号的方向
,得
这个不等式的解集在数轴上的表示如图
注意:(3)(4)的求解过程,类似于解方程两边都除以未知数的系数(未知数系数化为1),解不等式时要注意未知数系数的正负,以决定是否改变不等号的方向
不等式性质3
-4
改变
例2
某长方体形状的容器长5cm,宽3cm,
高10cm。容器内原有水的高度为3cm,
现准备向它继续注水。用V(单位:
)
表示新注入水的体积,写出V的取值范围。
解:新注入水的体积V与原有水的体积的和不能
超过容器的容积,即
V+3×5×3≤3×5×10
解得
V≤105
又由于新注入水的体积不能是负数,因此,
V的取值范围是
V≥0并且V≤105
在数轴上表示V的取值范围如图
0
105
(1)对自己说,你有什么收获?
(2)对同学说,你有什么温馨提示?
(3)对老师说,你还有什么困惑?
1.利用不等式的性质解下列不等式用数轴表示解集.
(1)
x+3>-1
解:根据不等式性质1,得
X<-7
(3)
4x>-12
解:根据不等式性质2,得
X>-3
解:根据不等式性质1,得
X>-4
(2)
6x<5x-7
2.某次“人与自然”的知识竟赛中共有20道题。对于每一道题,答对了得10分,答错了或不答扣5分,至少要答对几道题,其得分不少于80分?
解:设答对的题数是x,则答对或不答的题数为20-x,根据题意,得
10x
–
5(20
–
x)
≥
80
解这个不等式,得:
x
≥
12
答:……
3.
用炸药爆破时,如果导火索燃烧的速度是0.8
cm/s,人跑开的速度是每秒4
m,为了使点导火索的战士在爆破时能够跑到100
m以外的安全区域,这个导火索的长度应大于多少厘米?
解:设导火索的长度是x
cm
.根据题意,得
×4≥100.
答:导火索的长度应大于20
cm.
解得:
x≥20
新情境题
4.以下不等式中,不等号用对了么?
(1)3-a<6-a
(2)3a<6a
解:(1)3<6,根据不等式的性质1
将不等式两边同时减a,3-a<6-a
(2)3<6,当a>0时,根据不等式的性质2,3a<6a
当a<0时,根据不等式的性质3,3a>6a
5.如果关于x的不等式
(1-a)x>1-a
的解
集为
x<1
,那么请给出一个符合题意a的值
解:由(1-a)x>1-a
,不等式两边同时除以
1-a
,得到
x<1
不等号方向改变了,由不等式的性质3可知
1-a<0,a>1
可以取a=2
习
题
9.1
第5、9题
作业(课本P120)
第九章不等式与不等式组
9.1
不等式
在古代,我们的祖先就懂得了翘翘板的工作原理,并且根据这一原理设计出了一些简单机械,
并把它们用到了生活实践当中.
由此可见,“不相等”处处可见。
1.什么是等式?
2.等式的基本性质是什么?
等式的性质
等式的基本性质1:在等式两边都加上(或减去)同一个数或整式,结果仍相等.
如果a=b,那么a±c=b±c
等式的基本性质2:在等式两边都乘以或除以同一个数(除数不为0),结果仍相等.
如果a=b,那么ac=bc或
(c≠0),
不等式是否具有类似的性质呢?
探究一、请用”>””<”
填空并总结规律:
(1)5>3
,5+2
3+2,5-2
3-2
(2)-1<3,-1+2
3+2,-1-3
3-3
(3)6>2,6×5
2×5,
6×(-5)
2×(-5)
(4)-2<3,(-2)×6
3×6,
(-2)×(-6)
3×(-6)
>
>
<
<
>
<
>
<
由上面规律填空:
(1)当不等式两边加上或减去同一个数(正数或负数)时,不等号的方向
;
(2)当不等式两边乘同一个正数时,不等号的方向
;而乘同一个负数时,不等号的方向_________
不变
不变
改变
不等式基本性质1:不等式的两边都加上(或减去)同一个整式,
如果____,那么_________.
不等号的方向不变。
a>b
a±c>b±c
_________________
不等式基本性质2:不等式的两边都乘以(或除以)同一个____,不等号的方向____。
不等式基本性质3:不等式的两边都乘以(或除以)同一个____,不等号的方向____。
如果________,那么______________
不变
正数
a>b,c>0
ac>bc
(或
)
负数
改变
如果________,那么______________
a>b,c<0
ac
)
探究二、
比一比
想一想
不等式的性质和等式的性质有什么异同?
等式的性质
不等式的性质
1、等式两边同时加(或减)同一个数(或式子),结果仍相等。
1、不等式两边加(或减)同一个数(或式子),不等号的方向不变.
2.等式两边乘同一个数,或除以同一个不为0的数,结果仍相等。
2、不等式的两边乘(或除以)同一个正数,不等号的方向不变
3、不等式的两边乘(或除以)同一个负数,不等号的方向改变
不等式性质:
(1)不等式两边加(或减)同一个数(或式子),不等号的方向不变.
(2)不等式两边乘(或除以)同一个正数,不等号的方向不变.
(3)不等式两边乘(或除以)同一个负数,不等号的方向改变.
思考:(1)性质中的“不等号方向不变”和“不等号方向改变”的含义是什么?
(2)对比性质2和性质3,你能归纳出不等号的方向何时不变,何时改变吗?
若a>b,则
a±c>b±c
.
若a>b,则
a×c>b×c,
a÷c>
÷c
,(c>0)
若a>b,则
a×c
,(c<0)
注意:
①在利用不等式的基本性质进行变形时,当不等式的两边都乘以(或除以)同一个字母,字母代表什么数是问题的关键,这决定了是用不等式基本性质2还是基本性质3,也就是不等号是否要改变方向的问题;
②运用不等式基本性质3时,要变两个号,一个性质符号,另一个是不等号.
探究三、补例:1
利用不等式的性质,填”>”,“<”
(1)若a>b,则2a+1
2b+1;
(2)若-1.25y<10,则y
-8;
(3)若a
bc+c;
(4)若a>0,b<0,c<0,则(a-b)c
0.
>
>
<
<
解:(1)根据不等式基本性质1,两边都加上2,
得
x-2+2<3+2
x<5
(2)根据不等式基本性质1,两边都减去5x,
得
6x-5x<5x-1-5x
x<-1
解:(1)
∵a>b
∴两边都减去3,由不等式基本性质1
得
a-3>b-3
(2)
∵a>b,并且2>0
∴两边都除以2,由不等式基本性质2
得
(3)
∵a>b,并且-4<0
∴两边都乘以-4,由不等式基本性质3
得
-4a<-4b
不等式的基本性质1:
如果a
>b,那么a±c>b±c.就是说,不等式两边都加上
(或减去)同一个数(或式子),不等号方向不变。
不等式基本性质2:
如果a
>b,c
>
0
,那么
ac>bc(或
)
就是说不等式的两边都乘以(或除以)同一个正数,不等号的方向不变。
不等式基本性质3:
如果a>b,c<0
那么ac
1、(1)如果x-5>4,那么两边都
可得到x>9
(2)如果在-7<8的两边都加上9可得到
(3)如果在5>-2的两边都加上a+2可得到
(4)如果在-3>-4的两边都乘以7可得到
(5)如果在8>0的两边都乘以8可得到
(6)如果在
的两边都乘以14
可得到
加上5
2
<
17
a+7
>
a
-21>-28
64
>
0
2x>28+7x
2.用“>”或“<”在横线上填空,并在题后
括号内填写理由.若a
>
b;则
(1)
3a
3b;
(2)
a-8
b-8;
(3)
-2a
-2b;
(4)
2a-5
2b-5;
(5)
-3.5a-1
-3.5b-1.
>
>
<
<
>
不等式性质2
不等式性质1
不等式性质3
不等式性质1及2
不等式性质1及3
3、(1)如果在不等式8>0的两边都乘以―8可得到
(2)如果-3x>9,那么两边都除以-1/3可得到
(3)设m>n,用“>”或“<”填空:
m-5
n-5(根据不等式的性质
)
-6m
-6n(根据不等式的性质
)
-64
<
0
x
<
-3
>
1
<
3
4、判断正误:
(1)如果a>b,那么ac>bc。
(2)如果a>b,那么ac2>bc2。
(3)如果ac2>bc2,
那么a>b。
×
×
习
题
9.1
第4、6题
作业(课本P120)
第九章
不等式与不等式组
不等式基本性质1:不等式的两边都加上(或减去)同一个整式,
如果____,那么_________.
不等号的方向不变。
a>b
a±c>b±c
_________________
不等式基本性质2:不等式的两边都乘以(或除以)同一个____,不等号的方向____。
不等式基本性质3:不等式的两边都乘以(或除以)同一个____,不等号的方向____。
如果________,那么______________
不变
正数
a>b,c>0
ac>bc
(或
)
负数
改变
如果________,那么______________
a>b,c<0
ac
)
做一做:将下列不等式化成x
>
a或
x
<
a
的形式,并说出根据.
(1)
x-
7>26
(2)
3x
<
2x
+1
解:根据不等式的基本性质1
,
不等式两边都加上7,不等号方向不变,得,
x
>33
解:根据不等式的基本性质1,不等式两边都减去2x,不等号方向不变,得,
x
<
1
题目改为:利用不等式的性质解下列不等式,
并把解集在数轴上表示出来.
例1利用不等式的性质解下列不等式.
(1)
x-7>26
(2)
3x<2x+1
(3)
-
x﹥50 (4)
-
4x﹥3
3
2
探究一、
(1)
x-7>26
分析:解未知数为x的不等式,就是要使不等式逐步化为x﹥a或x﹤a的形式.
解:(1)为了使不等式x-7>26中不等号的一边变为x,根据不等式的性质1,不等式两边都加7,不等号的方向不变,得
x-7+7﹥26+7
x﹥33
这个不等式的解集在数轴上的表示如图,
(2)
3x<2x+1
3x-2x﹤2x+1-2x
x﹤1
为了使不等式3x<2x+1中不等号的一边变为x,根据
,不等式两边都减去
,不等号的方向
。
这个不等式的解在数轴上的表示如图
注意:解不等式时也可以“移项”,即把不等式的一边的某项变号后移到另一边,而不改变不等号的方向.
2x
不等式性质1
不变
得
x﹥75
这个不等式的解集在数轴的表示如图
不等式的两边都
除以2一3行吗?
(3)
x﹥50
(4)
-4x﹥3
为了使不等式-4x﹥3中的不等号的一边变为x,根据
,不等式两边都除以
,不等号的方向
,得
这个不等式的解集在数轴上的表示如图
注意:(3)(4)的求解过程,类似于解方程两边都除以未知数的系数(未知数系数化为1),解不等式时要注意未知数系数的正负,以决定是否改变不等号的方向
不等式性质3
-4
改变
例2
某长方体形状的容器长5cm,宽3cm,
高10cm。容器内原有水的高度为3cm,
现准备向它继续注水。用V(单位:
)
表示新注入水的体积,写出V的取值范围。
解:新注入水的体积V与原有水的体积的和不能
超过容器的容积,即
V+3×5×3≤3×5×10
解得
V≤105
又由于新注入水的体积不能是负数,因此,
V的取值范围是
V≥0并且V≤105
在数轴上表示V的取值范围如图
0
105
(1)对自己说,你有什么收获?
(2)对同学说,你有什么温馨提示?
(3)对老师说,你还有什么困惑?
1.利用不等式的性质解下列不等式用数轴表示解集.
(1)
x+3>-1
解:根据不等式性质1,得
X<-7
(3)
4x>-12
解:根据不等式性质2,得
X>-3
解:根据不等式性质1,得
X>-4
(2)
6x<5x-7
2.某次“人与自然”的知识竟赛中共有20道题。对于每一道题,答对了得10分,答错了或不答扣5分,至少要答对几道题,其得分不少于80分?
解:设答对的题数是x,则答对或不答的题数为20-x,根据题意,得
10x
–
5(20
–
x)
≥
80
解这个不等式,得:
x
≥
12
答:……
3.
用炸药爆破时,如果导火索燃烧的速度是0.8
cm/s,人跑开的速度是每秒4
m,为了使点导火索的战士在爆破时能够跑到100
m以外的安全区域,这个导火索的长度应大于多少厘米?
解:设导火索的长度是x
cm
.根据题意,得
×4≥100.
答:导火索的长度应大于20
cm.
解得:
x≥20
新情境题
4.以下不等式中,不等号用对了么?
(1)3-a<6-a
(2)3a<6a
解:(1)3<6,根据不等式的性质1
将不等式两边同时减a,3-a<6-a
(2)3<6,当a>0时,根据不等式的性质2,3a<6a
当a<0时,根据不等式的性质3,3a>6a
5.如果关于x的不等式
(1-a)x>1-a
的解
集为
x<1
,那么请给出一个符合题意a的值
解:由(1-a)x>1-a
,不等式两边同时除以
1-a
,得到
x<1
不等号方向改变了,由不等式的性质3可知
1-a<0,a>1
可以取a=2
习
题
9.1
第5、9题
作业(课本P120)
