人教版数学七年级下学期5.4 平移 同步练习卷含答案
文档属性
| 名称 | 人教版数学七年级下学期5.4 平移 同步练习卷含答案 |
|
|
| 格式 | zip | ||
| 文件大小 | 127.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-29 00:00:00 | ||
图片预览


文档简介
5.4
平移
一.选择题(共12小题)
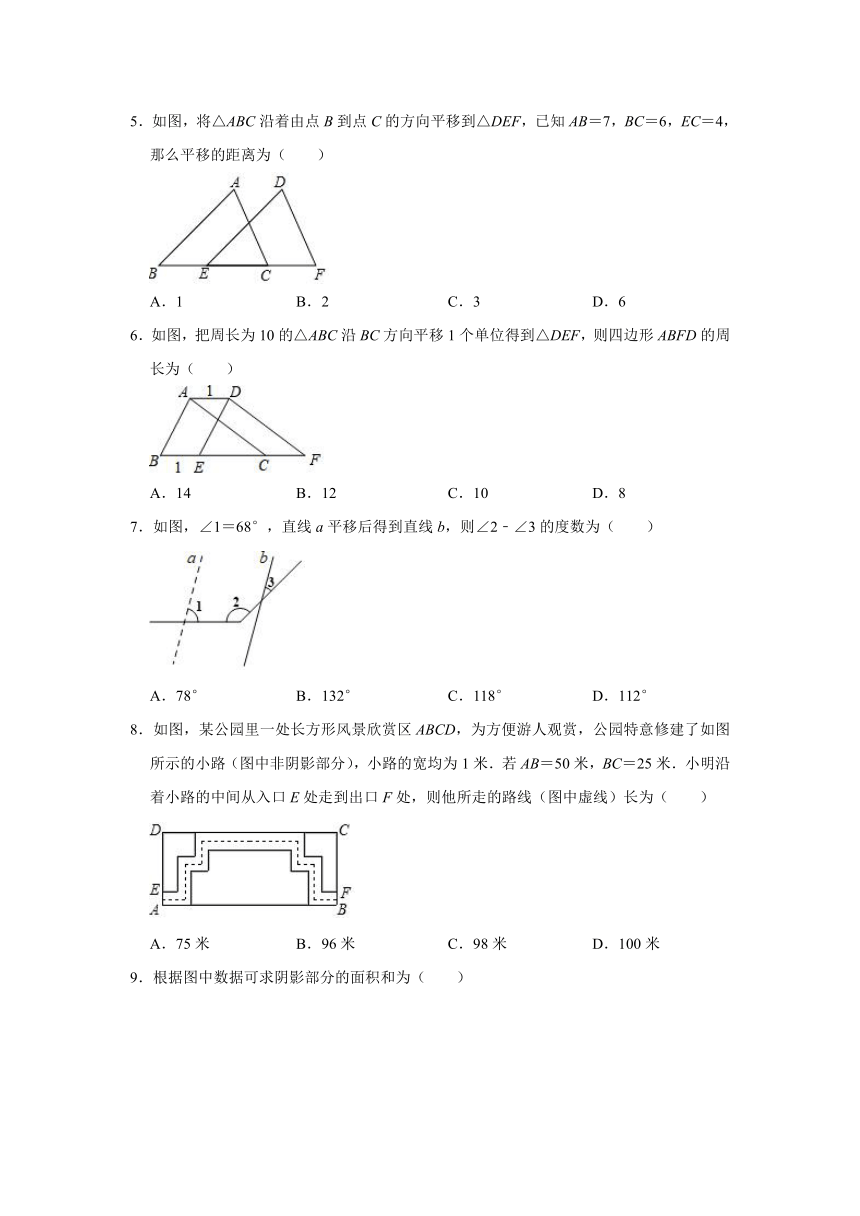
1.如图,一个圆柱体在正方体上沿虚线从左向右平移,平移过程中不变的是( )
A.主视图
B.左视图
C.俯视图
D.主视图和俯视图
2.如图属于平移位置变换的是( )
A.
B.
C.
D.
3.如图,将△ABC沿BC方向平移1cm得到△DEF,若△ABC的周长为8cm,则四边形ABFD的周长为( )
A.8cm
B.9cm
C.10cm
D.11cm
4.如图,将周长为12cm的△ABC沿边BC向右平移3cm得到△A′B′C′,则四边形ABC′A′的周长为( )
A.17cm
B.18cm
C.19cm
D.20cm
5.如图,将△ABC沿着由点B到点C的方向平移到△DEF,已知AB=7,BC=6,EC=4,那么平移的距离为( )
A.1
B.2
C.3
D.6
6.如图,把周长为10的△ABC沿BC方向平移1个单位得到△DEF,则四边形ABFD的周长为( )
A.14
B.12
C.10
D.8
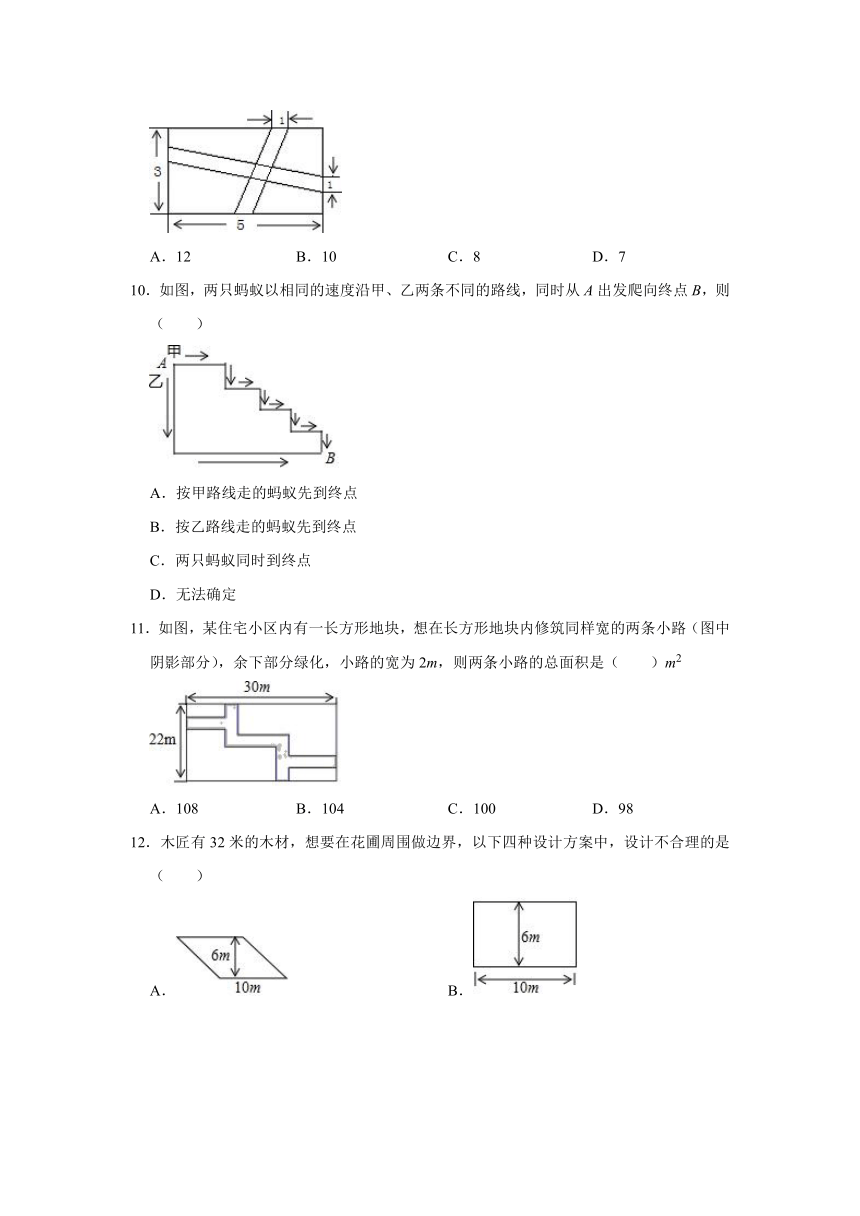
7.如图,∠1=68°,直线a平移后得到直线b,则∠2﹣∠3的度数为( )
A.78°
B.132°
C.118°
D.112°
8.如图,某公园里一处长方形风景欣赏区ABCD,为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小路的宽均为1米.若AB=50米,BC=25米.小明沿着小路的中间从入口E处走到出口F处,则他所走的路线(图中虚线)长为( )
A.75米
B.96米
C.98米
D.100米
9.根据图中数据可求阴影部分的面积和为( )
A.12
B.10
C.8
D.7
10.如图,两只蚂蚁以相同的速度沿甲、乙两条不同的路线,同时从A出发爬向终点B,则( )
A.按甲路线走的蚂蚁先到终点
B.按乙路线走的蚂蚁先到终点
C.两只蚂蚁同时到终点
D.无法确定
11.如图,某住宅小区内有一长方形地块,想在长方形地块内修筑同样宽的两条小路(图中阴影部分),余下部分绿化,小路的宽为2m,则两条小路的总面积是( )m2
A.108
B.104
C.100
D.98
12.木匠有32米的木材,想要在花圃周围做边界,以下四种设计方案中,设计不合理的是( )
A.
B.
C.
D.
二.解答题(共5小题)
13.如图,将三角形ABC沿射线BA方向平移到三角形A′B′C′的位置,连接AC′.
(1)AA′与CC′的位置关系为
;
(2)求证:∠A′+∠CAC′+∠AC′C=180°;
(3)设∠AC′B′=x,∠ACB=y,试探索∠CAC′与x,y之间的数量关系,并证明你的结论.
14.如图,在每个小正方形的边长均为1的方格纸中,三角形ABC的顶点都在方格纸的格点上,将三角形ABC先向左平移2格,再向上平移4格.
(1)请在图中画出平移后的三角形A′B′C′;
(2)求出三角形ABC的面积.
15.如图,在直角三角形ABC中,∠ACB=90°,AC=4cm,BC=3cm,△ABC沿AB方向平移至△DEF,若AE=8cm.DB=2cm.
(1)求△ABC沿AB方向平移的距离;
(2)求四边形AEFC的周长.
16.如图,将△ABC沿射线AB的方向平移2个单位到△DEF的位置,点A、B、C的对应点分别点D、E、F.
(1)直接写出图中与AD相等的线段.
(2)若AB=3,则AE=
.
(3)若∠ABC=75°,求∠CFE的度数.
17.两个全等的直角三角形重叠在一起,将其中的一个直角三角形沿着点B到点C的方向平移4个单位长度到△DEF的位置,如果AB=10,DH=3,求图中阴影部分的面积.
三.填空题(共2小题)
18.如图,将直角△ABC沿BC方向平移得到直角△DEF,其中AB=8,BE=6,DM=4,则阴影部分的面积是
.
19.如图,在△ABC中,将△ABC沿射线BC方向平移,使点B移动到点C,得到△DCF,连接AF,若△ABC的面积为4,则△ACF的面积为
.
参考答案
一.选择题(共12小题)
1.
B.
2.
A.
3.
C.
4.
B.
5.
B.
6.
B.
7.
D.
8.
C.
9.
C.
10.
C.
11.
C.
12.
A.
二.解答题(共5小题)
13.解:(1)由平移的性质可得:AA′∥CC′;
故答案为:AA′∥CC′;
(2)根据平移性质可知A'C'∥AC,AA'∥CC',
∴∠A'=∠BAC,∠BAC=∠ACC',
∴∠A'=∠ACC',
∵∠ACC'+∠CAC′+∠AC′C=180°,
∴∠A'+∠CAC'+∠AC'C=180°,
(3)结论:∠CAC'=x+y,
过点A作AD∥BC,交CC'于点D,
根据平移性质可知B'C'∥BC,
∴B'C'∥AD∥BC',
∴∠AC'B'=∠C'AD,∠ACB=∠DAC,
∴∠CAC'=∠C'AD+∠CAD=∠AC'B'+∠ACB=x+y,
即∠CAC'=x+y.
14.解:(1)如图,△A′B′C′为所作;
(2)三角形ABC的面积=×4×4=8.
15.解:(1)∵△ABC沿AB方向向右平移得到△DEF,
∴AD=BE=CF,BC=EF=3cm,
∵AE=8cm,DB=2cm,
∴AD=BE=CF==3(cm),即△ABC沿AB方向平移的距离是3cm;
(2)四边形AEFC的周长=AE+EF+CF+AC=8+3+3+4=18(cm).
16.解:(1)与AD相等的线段有:BE,CF;
(2)∵AB=3,将△ABC沿射线AB的方向平移2个单位到△DEF的位置,
∴BE=2,
则AE=BE+AB=5.
故答案为:5;
(3)∵由平移变换的性质得:BC∥EF,AE∥CF,
∴∠E=∠ABC=75°,
∴∠CFE+∠E=180°,
∴∠CFE=105°.
17.解:∵△DEF由△ABC平移而成,
∴△ABC≌△DEF,
∴图中阴影部分的面积与梯形ABEH的面积相等,
∵AB=10,DH=3,
∴EH=DE﹣DH=AB﹣DH=10﹣3=7,
∵BE=4,
∴S阴影=S梯形ABEH=(EH+AB)?BE=(10+7)×4=34.
三.填空题(共2小题)
18.解:∵直角△ABC沿BC方向平移得到直角△DEF,
∴DE=AB=8,
∵DM=4,
∴ME=DE﹣DM=8﹣4=4,
S阴影=S△DEF﹣S△MEC
=S△ABC﹣S△MEC
=S梯形ABEM
=×(4+8)×6
=36.
故答案为:36.
19.解:∵△ABC沿射线BC方向移动,使点B移动到点C,得到△DCF,
∴BC=CF,
∴S△ACF=S△ABC=4.
故答案为:4
平移
一.选择题(共12小题)
1.如图,一个圆柱体在正方体上沿虚线从左向右平移,平移过程中不变的是( )
A.主视图
B.左视图
C.俯视图
D.主视图和俯视图
2.如图属于平移位置变换的是( )
A.
B.
C.
D.
3.如图,将△ABC沿BC方向平移1cm得到△DEF,若△ABC的周长为8cm,则四边形ABFD的周长为( )
A.8cm
B.9cm
C.10cm
D.11cm
4.如图,将周长为12cm的△ABC沿边BC向右平移3cm得到△A′B′C′,则四边形ABC′A′的周长为( )
A.17cm
B.18cm
C.19cm
D.20cm
5.如图,将△ABC沿着由点B到点C的方向平移到△DEF,已知AB=7,BC=6,EC=4,那么平移的距离为( )
A.1
B.2
C.3
D.6
6.如图,把周长为10的△ABC沿BC方向平移1个单位得到△DEF,则四边形ABFD的周长为( )
A.14
B.12
C.10
D.8
7.如图,∠1=68°,直线a平移后得到直线b,则∠2﹣∠3的度数为( )
A.78°
B.132°
C.118°
D.112°
8.如图,某公园里一处长方形风景欣赏区ABCD,为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小路的宽均为1米.若AB=50米,BC=25米.小明沿着小路的中间从入口E处走到出口F处,则他所走的路线(图中虚线)长为( )
A.75米
B.96米
C.98米
D.100米
9.根据图中数据可求阴影部分的面积和为( )
A.12
B.10
C.8
D.7
10.如图,两只蚂蚁以相同的速度沿甲、乙两条不同的路线,同时从A出发爬向终点B,则( )
A.按甲路线走的蚂蚁先到终点
B.按乙路线走的蚂蚁先到终点
C.两只蚂蚁同时到终点
D.无法确定
11.如图,某住宅小区内有一长方形地块,想在长方形地块内修筑同样宽的两条小路(图中阴影部分),余下部分绿化,小路的宽为2m,则两条小路的总面积是( )m2
A.108
B.104
C.100
D.98
12.木匠有32米的木材,想要在花圃周围做边界,以下四种设计方案中,设计不合理的是( )
A.
B.
C.
D.
二.解答题(共5小题)
13.如图,将三角形ABC沿射线BA方向平移到三角形A′B′C′的位置,连接AC′.
(1)AA′与CC′的位置关系为
;
(2)求证:∠A′+∠CAC′+∠AC′C=180°;
(3)设∠AC′B′=x,∠ACB=y,试探索∠CAC′与x,y之间的数量关系,并证明你的结论.
14.如图,在每个小正方形的边长均为1的方格纸中,三角形ABC的顶点都在方格纸的格点上,将三角形ABC先向左平移2格,再向上平移4格.
(1)请在图中画出平移后的三角形A′B′C′;
(2)求出三角形ABC的面积.
15.如图,在直角三角形ABC中,∠ACB=90°,AC=4cm,BC=3cm,△ABC沿AB方向平移至△DEF,若AE=8cm.DB=2cm.
(1)求△ABC沿AB方向平移的距离;
(2)求四边形AEFC的周长.
16.如图,将△ABC沿射线AB的方向平移2个单位到△DEF的位置,点A、B、C的对应点分别点D、E、F.
(1)直接写出图中与AD相等的线段.
(2)若AB=3,则AE=
.
(3)若∠ABC=75°,求∠CFE的度数.
17.两个全等的直角三角形重叠在一起,将其中的一个直角三角形沿着点B到点C的方向平移4个单位长度到△DEF的位置,如果AB=10,DH=3,求图中阴影部分的面积.
三.填空题(共2小题)
18.如图,将直角△ABC沿BC方向平移得到直角△DEF,其中AB=8,BE=6,DM=4,则阴影部分的面积是
.
19.如图,在△ABC中,将△ABC沿射线BC方向平移,使点B移动到点C,得到△DCF,连接AF,若△ABC的面积为4,则△ACF的面积为
.
参考答案
一.选择题(共12小题)
1.
B.
2.
A.
3.
C.
4.
B.
5.
B.
6.
B.
7.
D.
8.
C.
9.
C.
10.
C.
11.
C.
12.
A.
二.解答题(共5小题)
13.解:(1)由平移的性质可得:AA′∥CC′;
故答案为:AA′∥CC′;
(2)根据平移性质可知A'C'∥AC,AA'∥CC',
∴∠A'=∠BAC,∠BAC=∠ACC',
∴∠A'=∠ACC',
∵∠ACC'+∠CAC′+∠AC′C=180°,
∴∠A'+∠CAC'+∠AC'C=180°,
(3)结论:∠CAC'=x+y,
过点A作AD∥BC,交CC'于点D,
根据平移性质可知B'C'∥BC,
∴B'C'∥AD∥BC',
∴∠AC'B'=∠C'AD,∠ACB=∠DAC,
∴∠CAC'=∠C'AD+∠CAD=∠AC'B'+∠ACB=x+y,
即∠CAC'=x+y.
14.解:(1)如图,△A′B′C′为所作;
(2)三角形ABC的面积=×4×4=8.
15.解:(1)∵△ABC沿AB方向向右平移得到△DEF,
∴AD=BE=CF,BC=EF=3cm,
∵AE=8cm,DB=2cm,
∴AD=BE=CF==3(cm),即△ABC沿AB方向平移的距离是3cm;
(2)四边形AEFC的周长=AE+EF+CF+AC=8+3+3+4=18(cm).
16.解:(1)与AD相等的线段有:BE,CF;
(2)∵AB=3,将△ABC沿射线AB的方向平移2个单位到△DEF的位置,
∴BE=2,
则AE=BE+AB=5.
故答案为:5;
(3)∵由平移变换的性质得:BC∥EF,AE∥CF,
∴∠E=∠ABC=75°,
∴∠CFE+∠E=180°,
∴∠CFE=105°.
17.解:∵△DEF由△ABC平移而成,
∴△ABC≌△DEF,
∴图中阴影部分的面积与梯形ABEH的面积相等,
∵AB=10,DH=3,
∴EH=DE﹣DH=AB﹣DH=10﹣3=7,
∵BE=4,
∴S阴影=S梯形ABEH=(EH+AB)?BE=(10+7)×4=34.
三.填空题(共2小题)
18.解:∵直角△ABC沿BC方向平移得到直角△DEF,
∴DE=AB=8,
∵DM=4,
∴ME=DE﹣DM=8﹣4=4,
S阴影=S△DEF﹣S△MEC
=S△ABC﹣S△MEC
=S梯形ABEM
=×(4+8)×6
=36.
故答案为:36.
19.解:∵△ABC沿射线BC方向移动,使点B移动到点C,得到△DCF,
∴BC=CF,
∴S△ACF=S△ABC=4.
故答案为:4
